Victor Cabanillas Zanini - Matemática aplicada a los negocios

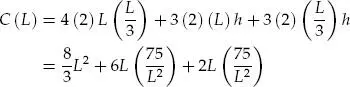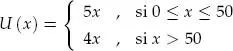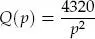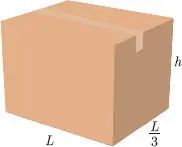
Figura 1.34

Ya que el volumen de la caja es de 25 m 3, tenemos:

Por lo tanto, la función costo de construcción es:

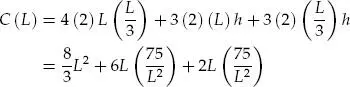
Simplificando, obtenemos:

El dominio de la función costo es 〈0; +∞〉.

Ejemplo 1.15

En el planeamiento de una cafetería, se estima que si hay espacio para 50 personas, las utilidades diarias serán de 5 dólares por persona. Sin embargo, si el espacio se habilita para más de 50 personas, las utilidades diarias por persona disminuirán en un 20 %. Si x es el número de personas que acuden a la cafetería, exprese el monto de las utilidades diarias como función de x y bosqueje el gráfico de la función.

Solución

Sea x el número de personas que acuden a la cafetería. Si x < 50, entonces, el problema nos dice que la utilidad total generada por x personas será de 5 x dólares. Pero si la cafetería se habilita para atender a más de 50 personas, la utilidad que genera cada una se reduce en 20 % (20 % de 5 dólares); es decir, cada persona generaría una utilidad de 4 dólares. Luego, la utilidad generada por x visitantes a la cafetería, sería de 4 x dólares cuando x > 50. De esta forma, la función utilidad queda definida por:

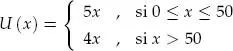
y su gráfica es:

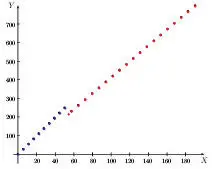
Figura 1.35

Aquí, la gráfica aparece con líneas punteadas, debido a que el dominio de la función está formado por números enteros no negativos, pues x representa el número de personas que acuden a la cafetería.

1.9. Ejercicios y problemas propuestos

1. Para construir una caja abierta, de base cuadrada, se necesitan $ 64. Si los lados de la caja cuestan $ 3 por m 2y la base, $ 4 por m 2, exprese su volumen en función de la longitud de un lado de la base. Indique su dominio.

2. El departamento de obras de una empresa está planeando construir una playa de estacionamiento rectangular de 9200 m 2de área. Para ello se construirá un cerco perimetral cuyo costo por metro de cerca es de $ 20. Si x denota el ancho del terreno, halle la función costo de cercado C ( x ).

3. Un negocio con capital original de $ 10 000 tiene ingresos y gastos semanales de $ 2000 y $ 1600, respectivamente. Si se retienen en el negocio todas las utilidades, exprese el capital del negocio al final de t semanas. Halle el dominio de la función obtenida. Grafique la función.

4. Un fabricante puede producir estantes a un costo de $ 80 la unidad. Las cifras de ventas indican que si los estantes se venden a x dólares la unidad, se venderán 500 – x estantes cada mes. Exprese la utilidad mensual del fabricante en función del precio de venta, grafique la función y determine el precio óptimo de venta.

5. Un fabricante de Gamarra vende 900 polos semanales al precio de 10 soles cada uno. El costo de cada polo es de 5 soles. El fabricante quiere aumentar el precio de su producto y, por los estudios de mercado realizados, se conoce que por cada 50 céntimos de incremento en el precio del polo se venderán 60 polos menos cada semana. Halle la función utilidad semanal del fabricante, indicando el dominio. Grafique la función.

6. Durante la sequía, los residentes de una ciudad tuvieron que hacer frente a una severa escasez de agua.

Para impedir el consumo excesivo de agua, la empresa encargada del servicio de agua potable y alcantarillado fijó drásticos aumentos en las tarifas. La tarifa mensual fue $ 5 por 10 m 3de agua para los primeros 30 m 3, $ 20 por cada 10 m 3para los 50 m 3siguientes y $ 50 por cada 10 m 3de allí en adelante.

a) Exprese la factura mensual en función de la cantidad de agua consumida.

b) Halle el dominio y grafique la función.

c) ¿Cuánto pagó la familia que consumió 85 m 3de agua?

7. Una compañía de autobuses, para su campaña Viajes de Promoción , ha adoptado la siguiente política de precios para quienes desean alquilar sus vehículos: para grupos formados por no más de 30 alumnos se cobrará la cantidad fija de $ 1500. Para grupos conformados entre 30 y 70 alumnos, cada alumno pagará $ 50 y tendrá un descuento de 50 centavos de dólar por cada alumno adicional a 30. La tarifa más baja de la compañía, $ 30 por alumno, se ofrecerá a grupos de 70 o más.

a) Exprese los ingresos de la compañía de autobuses como una función del número de alumnos que conforman el grupo.

b) Grafique la función ingreso.

c) ¿Cuál es el ingreso de la compañía, si el grupo tiene 68 alumnos?

8. Un envase que tendrá la forma de un cilindro circular recto debe contener 1π pulg 3de aceite de oliva. El costo de construcción de una pulg 2de las partes metálicas superior e inferior (base y tapa del envase) es dos veces el costo de construcción de una pulg 2de la superficie lateral de cartón. Exprese el costo de construcción del envase como función del radio, si el costo de la superficie lateral es de $ 0,02 por pulg 2. Halle el dominio.

9. Un anuncio para el cual se requieren márgenes de 3 pulgadas en las partes superior e inferior, y de 2 pulgadas en los lados, deberá tener 50 pulg 2para el material impreso. Si x es la longitud de la base del anuncio, exprese el área total del anuncio como función de x e indique su dominio.

10. Un campo petrolero tiene 20 pozos. Cada pozo ha estado produciendo 200 barriles diarios de petróleo. Se conoce que, por cada nuevo pozo perforado, la producción diaria de cada pozo disminuye en cinco barriles.

a) Escriba la producción diaria P del campo petrolero como función del número x de pozos nuevos que se perforan.

b) Trace la gráfica de y = P ( x ).

c) Mediante el gráfico de P , determine el valor de x que maximiza P .

11. Un importador de café estima que los consumidores locales comprarán:

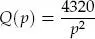
kilogramos de café a la semana cuando el precio sea de p dólares por kilogramo. Se estima que dentro de t semanas el precio será de p ( t ) = 0, 04 t 2+ 0, 2 t + 12 dólares por kilogramo.

a) Exprese la demanda de consumo semanal de café como una función de t .

b) Dentro de diez semanas, ¿cuántos kilogramos de café comprarán los consumidores al importador?

c) ¿En qué momento la demanda de café es de 30 kilogramos?

12. P ( x ) es la cantidad de cierto artículo, que se produce utilizando x kilogramos de un insumo A. Se conoce que: