Victor Cabanillas Zanini - Matemática aplicada a los negocios

Matemática aplicada a los negocios / Víctor Cabanillas, Tomás Núñez, Luis Huamán, Luis Toro y Jorge Urdanivia. Primera edición. Lima: Universidad de Lima, Fondo Editorial, 2021.

396 páginas: diagramas, gráficos.

Referencias: página 393.

1. Matemáticas. 2. Funciones (Matemáticas). 3. Modelos matemáticos. 4. Cálculo diferencial 5. Cálculo integral. I. Universidad de Lima. Fondo Editorial.

330.0151

M ISBN 978-9972-45-575-9

Matemática aplicada a los negocios

Primera edición impresa: septiembre, 2021

Primera edición digital: octubre, 2021

© Víctor Cabanillas Z., Tomás Núñez L., Luis Huamán R., Luis Toro M., Jorge Urdanivia E.

© De esta edición

Universidad de Lima

Fondo Editorial

Av. Javier Prado Este 4600,

Urb. Fundo Monterrico Chico, Lima 33 Apartado postal 852, Lima 100, Perú

Teléfono: 437-6767, anexo 30131

fondoeditorial@ulima.edu.pe

www.ulima.edu.pe

Diseño, edición y carátula: Fondo Editorial de la Universidad de Lima

Imagen de carátula: Shutterstock.com

Versión e-book 2021

Digitalizado y distribuido por Saxo.comPerú S. A. C.

https://yopublico.saxo.com/

Teléfono: 51-1-221-9998

Avenida Dos de Mayo 534, Of. 404, Miraflores

Lima - Perú

Se prohíbe la reproducción total o parcial de este libro, por cualquier medio, sin permiso expreso del Fondo Editorial.

ISBN 978-9972-45-575-9

Hecho el depósito legal en la Biblioteca Nacional del Perú n. o2021-11582

Índice

Presentación

Capítulo 1: Funciones elementales y modelos matemáticos

1.1. Introducción

1.1.1 Gráfico de una función

1.2. Funciones elementales

1.2.1 Función constante

1.2.2 Función lineal

1.2.3 Función cuadrática

1.2.4 Función raíz cuadrada

1.2.5 Función valor absoluto

1.3. Operaciones con funciones

1.4. Ejercicios resueltos

1.5. Funciones definidas por tramos

1.6. Ejercicios resueltos

1.7. Ejercicios propuestos

1.8. Modelos matemáticos

1.9. Ejercicios y problemas propuestos

Capítulo 2: Límites de funciones

2.1. Introducción

2.2. Definición y ejemplos

2.3. Cálculo de límites

2.4. Límites con indeterminación de forma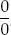

2.5. Ejercicios resueltos

2.6. Ejercicios propuestos

2.7. Límites laterales

2.8. Ejercicios resueltos

2.9. Ejercicios propuestos

2.10. Límites infinitos

2.10.1 Interpretación geométrica de los límites infinitos

2.11. Ejercicios propuestos

2.12. Límites al infinito

2.12.1 Límites al infinito de funciones racionales

2.12.2 Límites al infinito de funciones irracionales

2.12.3 Interpretación geométrica de los límites al infinito

2.13. Ejercicios resueltos

2.14. Ejercicios propuestos

2.15. Aplicaciones de los límites infinitos y al infinito

2.15.1 Problemas de aplicación resueltos

2.16. Ejercicios propuestos

2.17. Funciones continuas

2.18. Ejercicios y problemas propuestos

Capítulo 3: La derivada en el campo de los negocios

3.1. Introducción

3.2. La derivada: definición y ejemplos

3.3. Reglas de derivación

3.3.1 Derivada de una potencia

3.3.2 Derivada del producto

3.3.3 Derivada del cociente

3.3.4 Interpretación geométrica de la derivada

3.4. Ejercicios propuestos

3.5. Regla de la cadena

3.6. Ejercicios y problemas propuestos

3.7. Derivación implícita

3.8. Ejercicios y problemas propuestos

3.9. Derivadas de orden superior

3.10. Ejercicios propuestos

Capítulo 4: Aplicaciones de la derivada a los negocios

4.1. Introducción

4.2. Razón de cambio

4.3. Ejercicios y problemas propuestos

4.4. Análisis marginal

4.4.1 Costo marginal

4.4.2 Ingreso marginal

4.4.3 Utilidad marginal

4.5. Problemas propuestos

4.6. Regla de L’Hôpital

4.7. Ejercicios propuestos

4.8. Diferenciales

4.9. Problemas propuestos

4.10. Gráficas de funciones: criterio de la primera derivada

4.10.1 Criterio de la primera derivada

4.11. Problemas propuestos

4.12. Concavidad y criterio de la segunda derivada

4.12.1 Criterio de la segunda derivada

4.13. Problemas propuestos

4.14. Optimización de funciones

4.15. Problemas propuestos

Capítulo 5: Funciones trascendentes y sus derivadas

5.1. Introducción: el número e

5.1.1 El interés compuesto y el número e

5.2. Función exponencial

5.3. Función logarítmica

5.3.1 Propiedades de la función logarítmica

5.4. Derivadas de las funciones exponencial y logarítmica

5.5. Aplicaciones de las funciones exponencial y logarítmica

5.6. Problemas resueltos

5.7. Ejercicios y problemas propuestos

5.8. Derivadas de las funciones trigonométricas y sus inversas

5.8.1 Funciones trigonométricas

5.8.2 Derivadas de las funciones trigonométricas

5.8.3 Funciones trigonométricas inversas

5.8.4 Derivadas de las funciones trigonométricas inversas

5.9. Ejercicios propuestos

Capítulo 6: Métodos de integración y aplicaciones

6.1. Introducción

6.2. La integral indefinida

6.3. Ejercicios propuestos

6.4. Métodos de integración: método de sustitución o cambio de variables

6.5. Ejercicios propuestos

6.6. Métodos de integración: método de integración por partes

6.7. Ejercicios propuestos

6.8. Aplicaciones de la integral indefinida

6.9. Ejercicios y problemas propuestos

6.10. Integrales que contienen expresiones cuadráticas

6.11. Ejercicios propuestos

6.12. Integración por descomposición en fracciones parciales

6.13. Ejercicios y problemas resueltos

6.14. Ejercicios y problemas propuestos

Capítulo 7: La integral definida y sus aplicaciones en los negocios

7.1. Introducción

7.2. La integral definida

7.3. Ejercicios resueltos

7.4. Ejercicios propuestos

7.5. Aplicaciones de la integral definida: cálculo de áreas de regiones planas

7.6. Ejercicios resueltos

7.7. Ejercicios propuestos

7.8. Aplicaciones de la integral definida: integrales impropias

7.9. Ejercicios resueltos

7.10. Ejercicios propuestos

7.11. Aplicaciones de la integral definida: valor acumulado y valor promedio

7.12. Ejercicios resueltos

7.13. Ejercicios y problemas propuestos

7.14. Aplicaciones de la integral definida: excedentes del consumidor

7.15. Ejercicios resueltos

7.16. Ejercicios y problemas propuestos

7.17. Aplicaciones de la integral definida: excedente del productor

7.18. Ejercicios resueltos

7.19. Ejercicios y problemas propuestos

Respuestas a los ejercicios y problemas propuestos

Referencias

Acerca de los autores

Presentación

La matemática está cada vez más presente en el lenguaje diario de los profesionales de la administración, la economía, las finanzas, los negocios y las ciencias sociales. Los modelos matemáticos y las conclusiones que podamos extraer de estos juegan hoy en día un rol fundamental en la descripción del comportamiento cualitativo y cuantitativo de variables como el precio de un producto, su oferta y demanda, así como del costo, el ingreso y la utilidad. En tal sentido, el manejo del lenguaje matemático, desde el punto de vista de la interpretación de resultados, y no como mero cálculo, acompañado del uso de la tecnología, constituye un valor agregado en los profesionales de estas áreas.