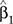Colección Textos Universitarios
Estadística aplicada a la ingeniería y los negocios
Primera edición digital, noviembre de 2016
© Rosa Millones, Emma Barreno, Félix Vásquez, Carlos Castillo
© Universidad de Lima
Fondo Editorial
Av. Javier Prado Este N. o4600,
Urb. Fundo Monterrico Chico, Lima 33, Perú
Apartado postal 852, Lima 100, Perú
Teléfono: 437-6767, anexo 30131
fondoeditorial@ulima.edu.pe
www.ulima.edu.pe
Diseño, edición y carátula: Fondo Editorial de la Universidad de Lima
Versión ebook 2017
Digitalizado y distribuido por Saxo.comPeru S.A.C.
https://yopublico.saxo.com/
Teléfono: 51-1-221-9998
Avenida Dos de Mayo 534, Of. 304, Miraflores
Lima - Perú
Se prohíbe la reproducción total o parcial de este libro sin permiso expreso del Fondo Editorial.
ISBN versión electrónica: 978-9972-45-356-4
Presentación
Capítulo 1. Distribuciones muestrales
1. Conceptos básicos
2. Muestra aleatoria
3. Tipos de muestreo
3.1 Muestreo probabilístico
3.1.1 Muestreo aleatorio simple
3.1.2 Muestreo sistemático
3.1.3 Muestreo estratificado
3.1.4 Muestreo por conglomerados
3.2 Muestreo no probabilístico
3.2.1 Muestreo por cuotas
3.2.2 Muestreo por conveniencia
3.2.3 Muestreo de juicio
4. Principales estadísticos
5. Distribución de la media muestral
6. Teorema central del límite
6.1 Aplicación del teorema central del límite a diferentes distribuciones
6.1.1 Distribución de Poisson
6.1.2 Distribución uniforme
7. Distribuciones de muestras pequeñas
7.1 Distribución Ji cuadrado
7.2 Distribución t de Student
7.3 Distribución F de Fisher
8. Distribuciones muestrales de un estadígrafo
8.1 Distribución de la media muestral con varianza poblacional conocida
8.2 Distribución de la media muestral con varianza poblacional desconocida
8.3 Distribución de una proporción muestral
8.4 Distribución de la varianza muestral
9. Distribuciones muestrales de dos muestras
9.1 Diferencia de medias muestrales con varianzas poblacionales conocidas
9.2 Diferencia de medias muestrales con varianzas poblacionales desconocidas
9.2.1 Varianzas poblacionales homogéneas
9.2.2 Varianzas poblacionales heterogéneas
9.3 Cociente de varianzas muestrales
9.4 Diferencia de proporciones muestrales
Problemas resueltos
Problemas propuestos
Capítulo 2. Estimación de parámetros
1. Definición
2. Propiedades de un buen estimador puntual
2.1 Insesgabilidad
2.2 Consistencia
2.3 Suficiencia
2.4 Eficiencia
3. Métodos de obtención de estimadores puntuales
3.1 Método de momentos
3.2 Método de máxima verosimilitud
4. Estimación por intervalos
4.1 Intervalo de confianza para la media poblacional
4.1.1 Caso 1: la varianza poblacional (σ 2) es conocida
4.1.2 Caso 2: la varianza poblacional (σ 2) es desconocida
4.2 Intervalo de confianza para π
4.3 Intervalo de confianza para la varianza poblacional μ
4.4 Intervalo de confianza para la diferencia de proporciones (σ 2)
4.5 Intervalo de confianza para una razón de varianzas 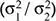
4.6 Intervalo de confianza para la diferencia de medias (μ 1– μ 2)
4.6.1 Varianzas poblacionales conocidas
4.6.2 Varianzas poblacionales desconocidas
Problemas resueltos
Problemas propuestos
Capítulo 3. Prueba de hipótesis
1. Definición
2. Clases de hipótesis
2.1 Hipótesis nula (H 0)
2.2 Hipótesis alternativa (H 1)
2.3 Prueba estadística de una hipótesis
3. Tipos de prueba
3.1 Prueba de cola izquierda o inferior
3.2 Prueba de cola derecha o superior
3.3 Prueba de dos colas o bilateral
4. Tipos de errores
4.1 Nivel de significación
4.2 Región crítica
4.3 Región de aceptación
4.4 Procedimiento para realizar una prueba de hipótesis referente a un parámetro θ
5. Prueba de hipótesis para los parámetros
5.1 Prueba de hipótesis para la media de una población (μ)
5.1.1 Cuando la varianza poblacional es conocida
5.1.2 Cuando la varianza poblacional es desconocida
5.2 Prueba de hipótesis para una proporción poblacional (π)
5.3 Prueba de hipótesis para la varianza de la población (σ 2)
5.4 Prueba de hipótesis para una razón de varianzas 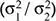
5.5 Prueba de hipótesis para la diferencia de dos medias (μ 1– μ 2)
5.5.1 Varianzas conocidas y muestras independientes
5.5.2 Varianzas desconocidas y muestras independientes
5.5.3 Muestras pareadas o dependientes
5.6 Prueba de hipótesis para la diferencia de dos proporciones
6. Funciones potencia y característica de operación
7. Prueba de bondad de ajuste
8. Prueba de independencia
Problemas resueltos
Problemas propuestos
Capítulo 4. Análisis de regresión
1. Definición
2. Tipos de relaciones
3. Tipos de modelo de regresión
3.1 Por la forma de influencia
3.2 Por el número de variables independientes que influyen en la variable respuesta
4. Análisis de regresión lineal simple
4.1 Metodología para la formulación de un modelo de regresión simple
4.2 Especificación del modelo de regresión lineal simple
4.2.1 Supuestos básicos del modelo de regresión lineal simple
4.3 Estimación de parámetros en un modelo de regresión lineal simple
4.3.1 Varianza de los estimadores 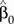 y
y 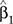
4.3.2 Intervalos de confianza para los parámetros
4.4 Tabla de análisis de varianza (ANOVA)
4.5 Verificación del modelo
4.5.1 Coeficiente de determinación (R 2)
4.5.2 Coeficiente de correlación lineal simple (r)
4.5.3 Pruebas de significación de las variables. Prueba T
4.5.4 Prueba de significación del modelo. Prueba F
5. Análisis de regresión lineal múltiple
5.1 Especificación del modelo de regresión lineal múltiple
5.1.1 Supuestos básicos del modelo de regresión lineal múltiple
5.2 Tabla de análisis de varianza (ANOVA)
5.3 Obtención de estimadores en un modelo de regresión lineal múltiple
5.3.1 Propiedades de los estimadores
5.3.2 Intervalos de confianza de los estimadores – RLM
5.4 Pruebas de verificación
5.4.1 Coeficiente de determinación múltiple (R2)
5.4.2 Prueba de significación del modelo – Prueba F
5.4.3 Prueba individual de las variables – Prueba T
Читать дальше




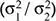
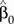 y
y