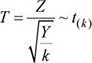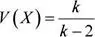6.1.2 Distribución uniforme
Sea X una variable aleatoria con distribución uniforme U (α; β), entonces
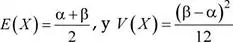
Si se toma una muestra de tamaño n la distribución de la media muestral  es
es
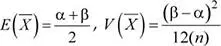 , es decir
, es decir

y por el teorema central del límite, resulta 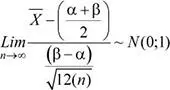
Ejemplo 6
Se sabe que el espesor de unas placas de acero es una variable aleatoria con distribución uniforme entre 12.52 y 12.88 milímetros.
a. Si se seleccionan 48 placas de acero, ¿cuál es la probabilidad de que la media muestral del espesor de las placas sea de por lo menos 12.68 mm?
b. ¿Cuál es la probabilidad de que 108 placas apiladas tengan una altura de a lo más 1.37 metros?
Solución
a. Sea X : Espesor, en milímetros, de una placa de acero, entonces
X ~ U (12.52;12.88), n = 48
Luego:
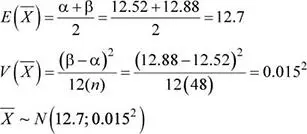
Por consiguiente, la probabilidad solicitada es
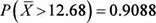
b. Sea X : Espesor, en milímetros, de una placa de acero, n = 108. Entonces,
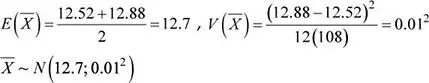
Luego, la probabilidad solicitada es: 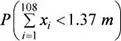
Como el valor de la variable se encuentra expresado en milímetros y la altura de las placas apiladas en metros; para calcular la probabilidad solicitada se realiza una conversión a metros, por lo tanto:
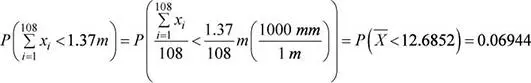
Nota.1 metro = 1000 milímetros.
7. DISTRIBUCIONES DE MUESTRAS PEQUEÑAS
Se dice que una muestra es pequeña cuando el muestreo se realiza con un número no mayor de 30 observaciones. Si la muestra es grande, se aproxima a una distribución normal . En esta sección se estudiarán las distribuciones Ji cuadrado , t de Student y F de Fisher .
7.1 Distribución Ji cuadrado
Sea x 1, x 2,..., x n una muestra aleatoria seleccionada de una población N (μ; σ 2)
Así, se tiene 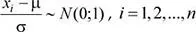 . Luego
. Luego 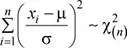
Propiedad:sea x 1, x 2,…, x n una muestra aleatoria seleccionada de una población 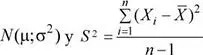 la varianza muestral. Entonces, se tiene
la varianza muestral. Entonces, se tiene 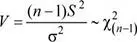
Esto es, la variable aleatoria V tiene una distribución χ 2con ( n - 1) grados de libertad.
Características: si X es una variable aleatoria con distribución Ji cuadrado , con m grados de libertad, entonces:
E ( X ) = m y V ( X ) = 2 m
El parámetro m de la distribución se conoce con el nombre de grados de libertad y es considerado como el número de valores que la variable puede tomar libremente con la condición de que la suma debe ser igual a un valor fijo, este valor se encuentra asociado con el tamaño de la muestra.
Ejemplo 7
El entrenador de un gimnasio realizó un estudio en relación con la distancia recorrida (en km) por los usuarios del gimnasio durante media hora de ejercicio en la caminadora mecánica. Como resultado del estudio se determinó que las distancias recorridas presentan una distribución normal con media de 5.2 km y una desviación estándar de 0.4 km. Determine la probabilidad de que la desviación estándar muestral de la distancia recorrida durante media hora de ejercicio por parte de 28 usuarios del gimnasio seleccionados al azar se encuentre entre 0.36 y 0.44 km.
Solución
Sea X : Distancia recorrida, en km, durante media hora de ejercicio en la caminadora mecánica, por parte del usuario del gimnasio. Luego, se tiene:
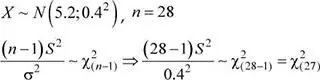
Por consiguiente,
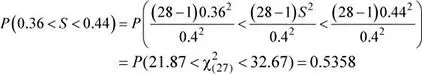
Interpretación:la probabilidad de que la desviación estándar muestral de la distancia recorrida se encuentre entre 0.36 y 0.44 km es de 0.5358.
7.2 Distribución t de Student
Sean Z ~ N (0;1) e 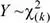 variables aleatorias independientes. Luego, la distribución de la variable aleatoria T es,
variables aleatorias independientes. Luego, la distribución de la variable aleatoria T es,
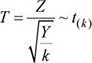
Así, la variable T tiene distribución t con k grados de libertad.
Características:
Si X ∼ t (k), entonces
E ( X ) = 0; para k > 1
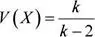
La distribución t de Student es muy similar a la distribución normal , ya que ambas varían en el conjunto de los números reales, aunque la distribución t presenta una mayor dispersión. Sin embargo, la varianza de la distribución t se aproxima a la unidad (1) cuando k es un número muy grande.
Читать дальше

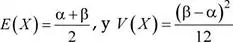
 es
es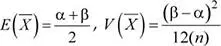 , es decir
, es decir
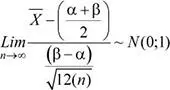
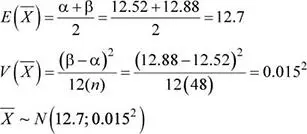
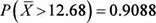
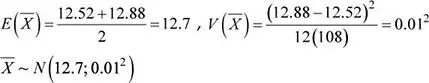
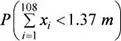
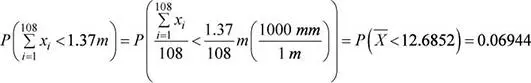
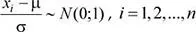 . Luego
. Luego 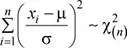
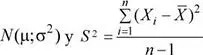 la varianza muestral. Entonces, se tiene
la varianza muestral. Entonces, se tiene 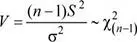
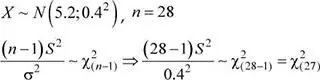
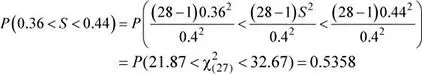
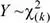 variables aleatorias independientes. Luego, la distribución de la variable aleatoria T es,
variables aleatorias independientes. Luego, la distribución de la variable aleatoria T es,