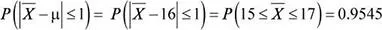Luego, la probabilidad solicitada es: P (Gasto excesivo) = P (  ≥ 124)
≥ 124)
Haciendo uso del software Minitab:
• Graph / Probability Distribution Plot …, seleccionar View Probability.
• Distribution: Normal. Mean: 120. Standard deviation: 2.5
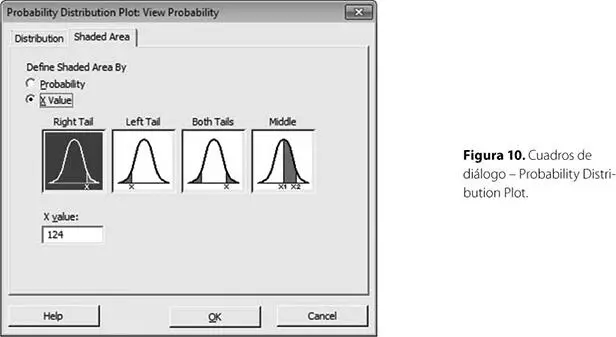
• Shaded Area: Seleccionar X value y Right Tail. X value: 124
Lo anteriormente expuesto se aprecia en la figura 10.
La probabilidad resultante se aprecia en la figura 11.
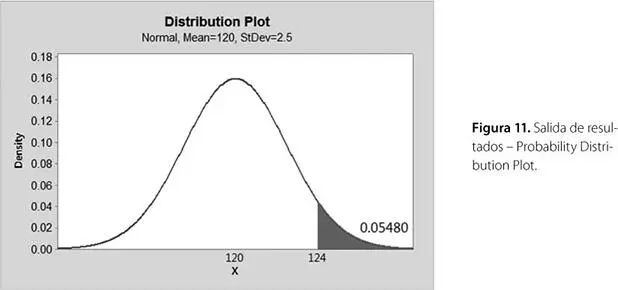
Luego: P (Gasto excesivo) = P (  ≥ 124) = 0.0548
≥ 124) = 0.0548
Interpretación: la probabilidad de que se incurra en un gasto excesivo es de 0.0548.
c. Del ítem (a):  ∼ N (120;2.5 2)
∼ N (120;2.5 2)
Luego, la probabilidad solicitada es: P (Gasto moderado) = P (117 ≤  ≤ 124)
≤ 124)
Al usar el software Minitab:
• Graph / Probability Distribution Plot …, seleccionar View Probability.
• Distribution: Normal. Mean: 120. Standard deviation: 2.5
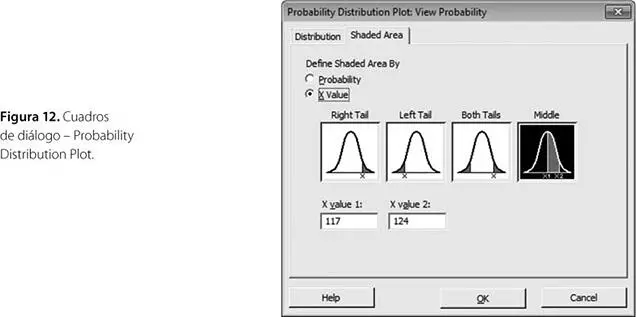
• Shaded Area: Seleccionar X value y Middle. X value 1: 117, X value 2 = 124
Lo anteriormente expuesto se aprecia en la figura 12.
La probabilidad resultante se aprecia en la figura 13.
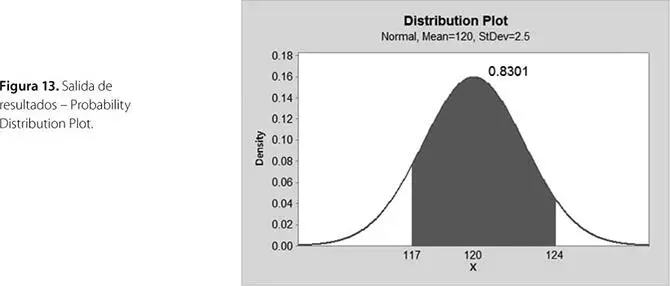
Luego: P (Gasto moderado) = P (117 ≤  ≤ 124) = 0.8301
≤ 124) = 0.8301
Interpretación:existe una probabilidad de 0.8301 de que la empresa presente gastos moderados.
d. Hallar el valor del tamaño de muestra n , tal que P (115 <  < 125) = 0.96
< 125) = 0.96
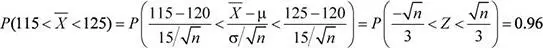
Como la distribución normal estándar es simétrica respecto del origen de coordenadas, se tiene que las probabilidades idénticas de ambos extremos de la gráfica (colas) deben sumar 0.04, es decir, la diferencia con respecto a la unidad.
Al hacer uso del software Minitab:
• Graph / Probability Distribution Plot …, seleccionar View Probability.
• Distribution: Normal. Mean: 120. Standard deviation: 2.5
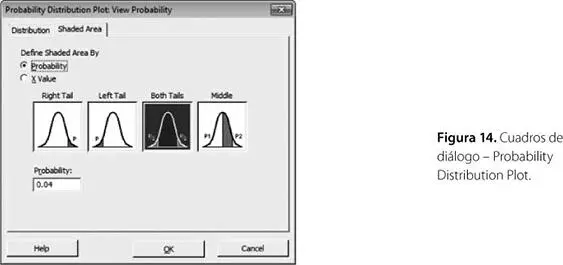
• Shaded Area: Seleccionar Probability y Both Tails. Probability: 0.04
Lo anteriormente expuesto se aprecia en la figura 14.
El valor de la abscisa resultante se aprecia en la figura 15.
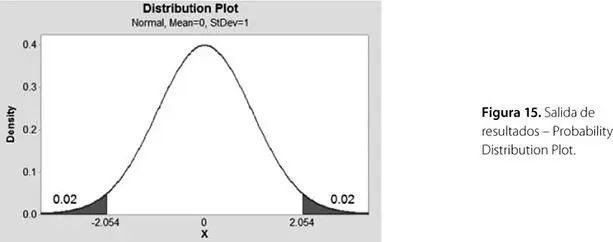
Se debe igualar el valor de la abscisa correspondiente:
Entonces: 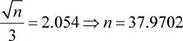
Interpretación:se deberían seleccionar 38 equipos de cómputo.
6.1 Aplicación del teorema central del límite a diferentes distribuciones
El teorema central del límite es útil para aproximar la distribución de la media muestral (  ) a una distribución normal, cuando la muestra aleatoria es obtenida de diferentes distribuciones de probabilidad para valores grandes del tamaño n de la muestra.
) a una distribución normal, cuando la muestra aleatoria es obtenida de diferentes distribuciones de probabilidad para valores grandes del tamaño n de la muestra.
6.1.1 Distribución de Poisson
Sea la variable aleatoria X ~ P (λ), con E ( X ) = λ, y V ( X = λ
Si se seleccionan muestras de tamaño n , con n suficientemente grande, la distribución de la media muestral es:
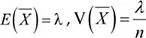 . Es decir:
. Es decir: 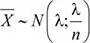
y por el teorema central del límite se tiene
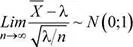
Ejemplo 5
M-Design es una empresa que brinda el servicio de pintura personalizada de motos y cuatrimotores. Luego del estudio se determinó que el número de personas interesadas en el servicio ofrecido, clientes que se apersonan o realizan llamadas para consultar por dicho servicio, presenta una distribución de Poisson con una media de 16 personas por día. Suponga que se seleccionan al azar 64 días y se registra el número diario de personas interesadas, ¿cuál es la probabilidad de que la media muestral de personas interesadas difiera de la media poblacional en a lo más 1 persona?
Solución
Se define:
X : Número diario de personas interesadas en el servicio ofrecido.
X ~ Poisson (λ = 16)
Como 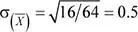 , por el teorema central del límite:
, por el teorema central del límite:  ~ N (16;0.5 2)
~ N (16;0.5 2)
Luego, la probabilidad solicitada es:
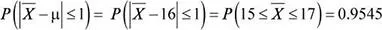
Interpretación:la probabilidad de que la media muestral difiera de la media poblacional, en a lo más 1 persona es de 0.9545.
Читать дальше

 ≥ 124)
≥ 124)



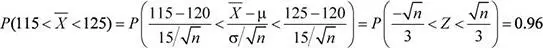


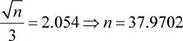
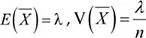 . Es decir:
. Es decir: 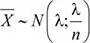
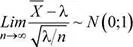
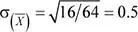 , por el teorema central del límite:
, por el teorema central del límite: