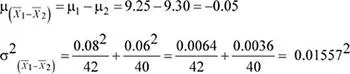1 ...7 8 9 11 12 13 ...25 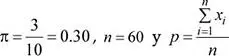 proporción muestral de tabletas de marca en análisis.
proporción muestral de tabletas de marca en análisis.
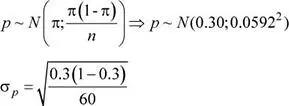
Luego, la probabilidad solicitada es: P ( p > 0.35) = 0.1992
Interpretación: la probabilidad de que la proporción de tabletas de dicha marca sea mayor que 0.35 es de 0.1992 aproximadamente.
b. Dado que: 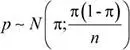 , entonces, para calcular el valor de n que verifica que
, entonces, para calcular el valor de n que verifica que
P (| p - π| ≤ 0.08) = 0.90, se tiene
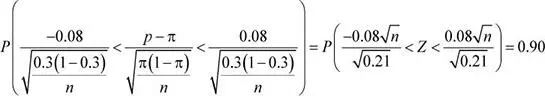
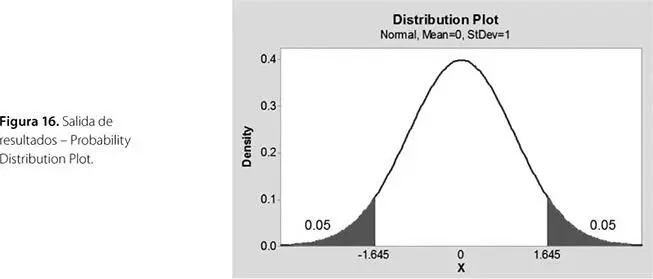
Como Z ~ N (0;1) es simétrica con respecto al origen, entonces la probabilidad de ambas colas es igual a 0.10. Véase figura 16.
Luego: 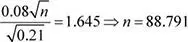
Interpretación:Se deben seleccionar 89 tabletas.
8.4 Distribución de la varianza muestral
Sea x 1, x 2,…, x n una muestra aleatoria seleccionada, con reemplazo, de una población con distribución normal : N (μ; σ 2), y sea: 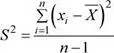
Entonces, la variable 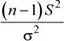 tiene una distribución Ji cuadrado con ( n - 1) grados de libertad.
tiene una distribución Ji cuadrado con ( n - 1) grados de libertad.
Propiedades:para una muestra aleatoria seleccionada de una población con distribución normal : N (μ; σ 2) se tiene:
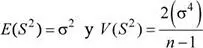
Ejemplo 13
Los montos de las transacciones realizadas en una agencia de barrio de una reconocida entidad bancaria, presentan una distribución normal con una desviación estándar poblacional de S/. 45.
a. ¿Cuál será la probabilidad de que las 37 próximas transacciones presenten una desviación estándar muestral de a lo más S/. 51?
b. Sobre la base de una muestra de 46 transacciones se ha estimado que existe una probabilidad de 0.15 de que la varianza sea de por lo menos k soles 2. Determine el valor de k .
Solución
a. Sea X : Monto (en S/.) de la transacción realizada en una agencia de barrio, y X ~ N (μ; 45 2), n = 37
Como 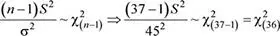
Luego, la probabilidad solicitada es
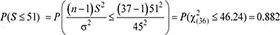
b. En este caso, se tiene:
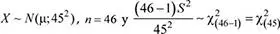
De acuerdo a los datos del problema se tiene: P ( S 2≥ k ) = 0.15
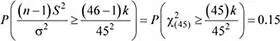
De donde: 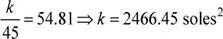
9. DISTRIBUCIONES MUESTRALES DE DOS MUESTRAS
Cuando se trata de comparar dos poblaciones de acuerdo a una característica de interés, se comparan las muestras aleatorias tomadas de ambas poblaciones.
9.1 Diferencia de medias muestrales con varianzas poblacionales conocidas
Sean: 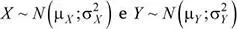 dos variables aleatorias independientes. Si se seleccionan muestras con reemplazo de tamaño n x y n y , y se obtienen las distribuciones de sus medias muestrales, se tiene:
dos variables aleatorias independientes. Si se seleccionan muestras con reemplazo de tamaño n x y n y , y se obtienen las distribuciones de sus medias muestrales, se tiene:
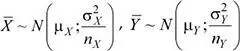
La distribución de la diferencia de las medias muestrales está dada por:
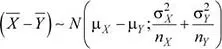
Donde la esperanza y varianza de esta diferencia son:
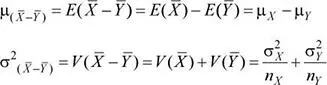
Nota.La expresión 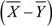 representa a una variable aleatoria.
representa a una variable aleatoria.
Ejemplo 14
Los ladrillos para techo producidos en las plantas A y B de la empresa Blokart presentan medias y varianzas poblacionales conocidas: μ 1= 9.25 kg, = σ 1= 0.08 kg, y = μ 2= 9.30 kg y σ 2= 0.06 kg. Se seleccionan 42 y 40 ladrillos para techo producidos en las plantas A y B, respectivamente; calcule la probabilidad de que la diferencia del peso promedio de los ladrillos obtenidos en las muestras de las plantas A y B difiera en a lo más 30 gramos de la diferencia de medias poblacionales.
Solución
X 1: Peso (en kg) de ladrillos para techo de la planta A. μ 1= 9.25, σ 1= 0.08, n 1= 42.
X 2: Peso (en kg) de ladrillos para techo de la planta A. μ 2= 9.30, σ 2= 0.06, n 2= 40.
La distribución de la diferencia de medias muestrales es:
(  1-
1-  2) ~ N (– 0.05;0.01557 2)
2) ~ N (– 0.05;0.01557 2)
donde
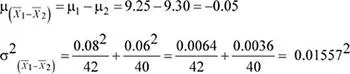
Luego, la probabilidad solicitada es: P (|  1-
1-  2) - (μ 1- μ 2)|≤ 0.03); 0.03 kg, equivalente a 30 gramos.
2) - (μ 1- μ 2)|≤ 0.03); 0.03 kg, equivalente a 30 gramos.
Читать дальше

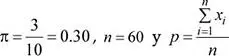 proporción muestral de tabletas de marca en análisis.
proporción muestral de tabletas de marca en análisis.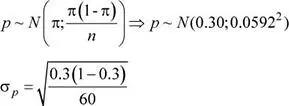
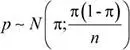 , entonces, para calcular el valor de n que verifica que
, entonces, para calcular el valor de n que verifica que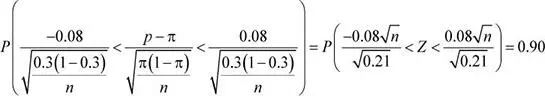
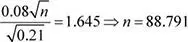

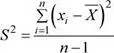
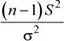 tiene una distribución Ji cuadrado con ( n - 1) grados de libertad.
tiene una distribución Ji cuadrado con ( n - 1) grados de libertad.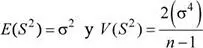
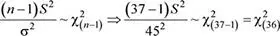
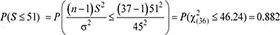
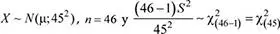
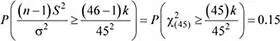
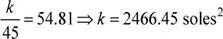
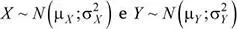 dos variables aleatorias independientes. Si se seleccionan muestras con reemplazo de tamaño n x y n y , y se obtienen las distribuciones de sus medias muestrales, se tiene:
dos variables aleatorias independientes. Si se seleccionan muestras con reemplazo de tamaño n x y n y , y se obtienen las distribuciones de sus medias muestrales, se tiene: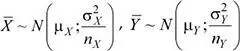
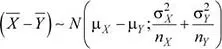
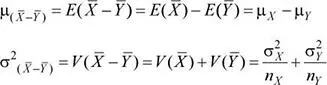
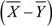 representa a una variable aleatoria.
representa a una variable aleatoria. 1-
1-