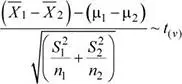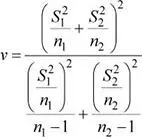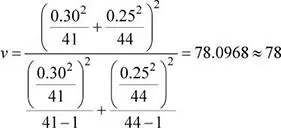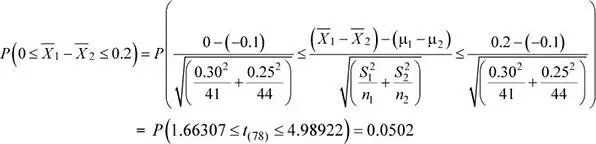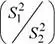1 ...8 9 10 12 13 14 ...25 P (|  1-
1-  2) - (-0.05)| ≤ 0.03) = P(-0.08 ≤
2) - (-0.05)| ≤ 0.03) = P(-0.08 ≤  1-
1-  2≤ -0.02) = 0.946
2≤ -0.02) = 0.946
9.2 Diferencia de medias muestrales con varianzas poblacionales desconocidas
En el caso de que las varianzas 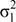 y
y 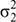 sean desconocidas, estas varianzas pueden ser homogéneas o heterogéneas.
sean desconocidas, estas varianzas pueden ser homogéneas o heterogéneas.
9.2.1 Varianzas poblacionales homogéneas 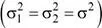
Para este caso, la variable aleatoria 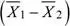 tiene la siguiente distribución:
tiene la siguiente distribución:
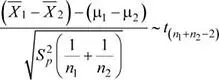
donde 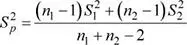 es la varianza ponderada de las 2 muestras.
es la varianza ponderada de las 2 muestras.
Ejemplo 15
El automóvil modelo Saux se comercializa en 2 modelos: A y B, los que al tener distintos pesos presentan un diferente rendimiento de combustible. El rendimiento tiene distribución normal con media 19.6 y 19.2 kilómetros por litro (en km/l) de combustible para los modelos A y B, respectivamente. Las varianzas poblacionales de los modelos A y B se desconocen pero se ha determinado que son homogéneas y se estimaron en 1.8 2y 2.0 2(km/l) 2, respectivamente. Se realizarán pruebas con muestras aleatorias de 37 automóviles modelo A y 34 modelo B. Determine la probabilidad de que la media muestral del rendimiento de combustible de los automóviles modelo A sea menor a la media muestral de los automóviles modelo B.
Solución
X 1: Rendimiento (en km/l) de combustible de los autos Saux modelo A. μ 1= 19.6, S 1= 1.8, n 1= 37.
X 2: Rendimiento (en km/l) de combustible de los autos Saux modelo B. μ 2= 19.2, S 2= 2.0, n 2= 34.
Dado que
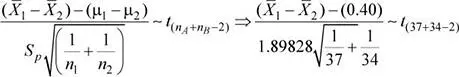
donde 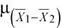 = μ 1- μ 2= 19.6 – 19.2 = 0.4
= μ 1- μ 2= 19.6 – 19.2 = 0.4
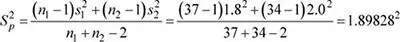
Luego, la probabilidad solicitada es
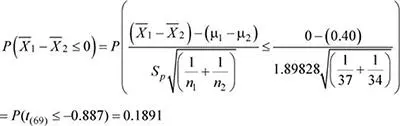
9.2.2 Varianzas poblacionales heterogéneas 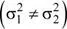
En este caso la distribución de la variable aleatoria 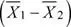 es
es
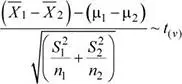


Donde V corresponde a los grados de libertad: 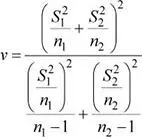
Nota.El valor de los grados de libertad ( V ) se redondea al entero inmediato inferior.
Ejemplo 16
Para llegar a un determinado lugar turístico ubicado en la provincia de Yauyos existen dos rutas. Los automóviles que van desde Lima por la ruta centro presentan un tiempo de viaje que se distribuye como una normal: μ 1= 8.4 horas , S 1= 0.30 h , y los automóviles que van por la ruta sur presentan un tiempo de viaje que también se distribuye como una normal: μ 2= 8.5 h , S 2= 0.25 h . Si se seleccionan 41 y 44 automóviles que se dirigen al mencionado lugar turístico por las rutas centro y sur, respectivamente, ¿cuál es la probabilidad de que la media muestral del tiempo de viaje de los automóviles que van por la ruta centro sea mayor, en a lo más 12 minutos, en comparación con los que van por la ruta sur? Suponga varianzas poblacionales desconocidas pero heterogéneas.
Solución
X 1: Tiempo de viaje, en horas, de los automóviles por la ruta centro. μ 1= 8.4, S 1= 0.30, n 1= 41.
X 2: Tiempo de viaje, en horas, de los automóviles por la ruta sur. μ 2= 8.5, S 2= 0.25, n 2= 44.
Dado que 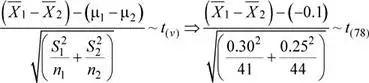
donde 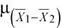 = μ 1- μ 2= 8.4 - 8.5 = -0.1
= μ 1- μ 2= 8.4 - 8.5 = -0.1
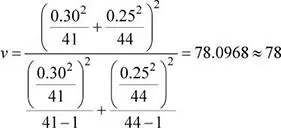
Luego, la probabilidad solicitada es P (0 ≤  1-
1-  2≤ 0.2)
2≤ 0.2)
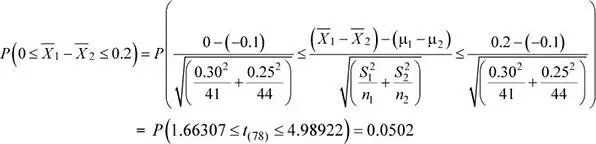
9.3 Cociente de varianzas muestrales 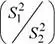
Читать дальше

 1-
1- 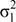 y
y 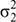 sean desconocidas, estas varianzas pueden ser homogéneas o heterogéneas.
sean desconocidas, estas varianzas pueden ser homogéneas o heterogéneas.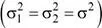
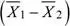 tiene la siguiente distribución:
tiene la siguiente distribución: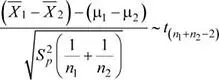
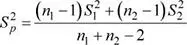 es la varianza ponderada de las 2 muestras.
es la varianza ponderada de las 2 muestras.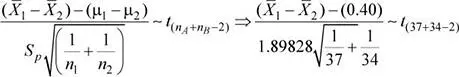
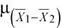 = μ 1- μ 2= 19.6 – 19.2 = 0.4
= μ 1- μ 2= 19.6 – 19.2 = 0.4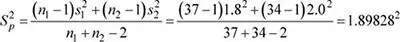
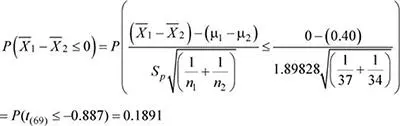
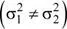
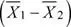 es
es