Victor Cabanillas Zanini - Matemática aplicada a los negocios
Здесь есть возможность читать онлайн «Victor Cabanillas Zanini - Matemática aplicada a los negocios» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на испанском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Matemática aplicada a los negocios
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Matemática aplicada a los negocios: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Matemática aplicada a los negocios»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Los autores, docentes de amplia trayectoria en las aulas universitarias, presentan, a través de sus siete capítulos, los conceptos del análisis matemático de manera intuitiva y didáctica.
El capítulo 1 contiene una revisión de las funciones elementales e inicia el estudio de los modelos matemáticos. En el capítulo 2 se explican las nociones de límite y continuidad de una función y sus aplicaciones. En el capítulo 3 se examina la derivada de una función y se estudian las reglas de derivación, la regla de la cadena, la derivación implícita y las derivadas de orden superior. El capítulo 4 estudia las aplicaciones de la derivada a los negocios. La derivada de las funciones trascendentes y sus aplicaciones se desarrollan en el capítulo 5. En el capítulo 6 se aborda la integral indefinida y los principales métodos de integración. Finalmente, en el capítulo 7 se presenta la integral definida y varias de sus aplicaciones, así como las integrales impropias.
Al final de cada sección el lector encontrará problemas y ejercicios propuestos para afianzar lo aprendido. Y en las páginas finales se han incluido sus respectivas respuestas.

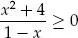
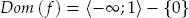
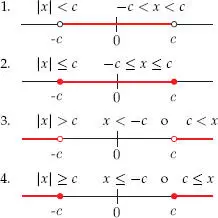
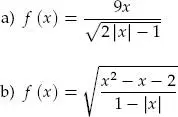
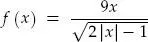 deben satisfacer la condición 2 | x | – 1 > 0. Es decir, | x | >
deben satisfacer la condición 2 | x | – 1 > 0. Es decir, | x | >  . Por lo tanto, el dominio de f es:
. Por lo tanto, el dominio de f es: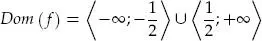
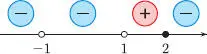
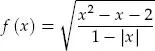 deben satisfacer:
deben satisfacer: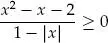
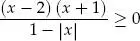
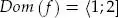
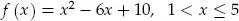
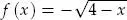
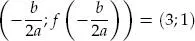
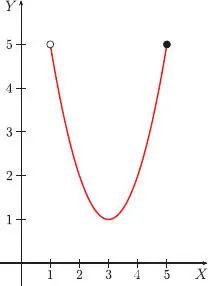
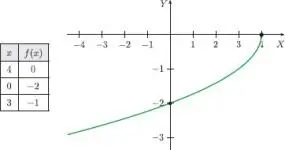
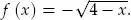 Por definición de la raíz cuadrada, debemos considerar que 4 – x ≥ 0; es decir, x ≤ 4. Así, el dominio de f es el intervalo 〈–∞; 4].
Por definición de la raíz cuadrada, debemos considerar que 4 – x ≥ 0; es decir, x ≤ 4. Así, el dominio de f es el intervalo 〈–∞; 4].