Juan Egoavil Vera - Fundamentos de matemática

( )

c. El grueso de un libro y el número de páginas, es una proporción directa.

( )

d. La representación gráfica de dos magnitudes directamente proporcionales es una recta que pasa por el origen.

( )

e. Dada una razón, existen otras razones iguales.

( )

f. Si M 1es DP a M 2, entonces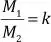

( )

2. A continuación se presentan diversas situaciones en las que intervienen proporcionales. Decida si se trata de magnitudes directa o inversamente proporcionales, coloque en el espacio indicado una D (directamente) o una I (inversamente) según sea el caso.

a. Cantidad de manzanas y su peso

( )

b. Número de bebidas y sus consumidores

( )

c. Número de personas trabajando y tiempo empleado en terminar el trabajo

( )

d. Cantidad de litros de bencina y el precio respectivo

( )

e. Número de baldosas para cubrir una determinada superficie y su tamaño

( )

f. Número de horas trabajadas y el sueldo ganado

( )

g. Número de ejercicios de matemáticas y el tiempo empleado en solucionarlos

( )

h. Cantidad de forraje (alimento) y número de animales por alimentar

( )

i. Días que alcanzan las provisiones y número de personas por alimentar

( )

j. Mejor respuesta en una evaluación y su nota.

( )

Habilidades de cálculo

1. Complete la siguiente tabla sabiendo que la proporcionalidad entre las magnitudes es directa.

¿Cuánto corresponde a 1? ...................

2. Complete la siguiente tabla sabiendo que la proporcionalidad entre las magnitudes es inversa.

¿Cuánto corresponde a 1? ...................

3. Reparta 600 en partes directamente proporcionales a 1, 2 y 3.

4. Reparta 78 en partes inversamente proporcionales a 2, 3 y 4.

5. Reparta 518 en partes inversamente proporcionales a 8, 10 y 12.

6. Compruebe si las siguientes magnitudes son inversamente proporcionales y en caso afirmativo señala cuál es la constante de proporcionalidad inversa:

a.

b.

c.

Modelación

Resuelva los siguientes problemas:

1. A una velocidad promedio de 75 km/h un vehículo demora 9 horas en ir de una ciudad a otra. ¿Cuántas horas tardaría si aumentara el promedio de su velocidad en 15 km/h?

2. Diez toneles iguales contienen 800 litros de vino ¿cuántos toneles son necesarios para almacenar 36 000 litros de vino?

3. 12,5 m de alambre cuestan $ 32 025. ¿Cuánto cuestan 8 m?, ¿y cuál es el precio de 50 cm del mismo alambre?

4. En un establo hay vacas que consumen 35 fardos de pasto en 40 días ¿en cuántos días consumirán 28 fardos?

5. Un cajón que pesa 9,6 kg contiene 1152 clavos ¿cuántos clavos, del mismo tamaño de los anteriores, habrá en un cajón que pesa 17 kg?

6. En un paseo que hicieron 24 alumnos consumieron 16 bebidas. Si al paseo hubieran ido 39 alumnos ¿cuántas bebidas habrían consumido?

7. El pavimento de un tramo de la carretera lo hacen 6 obreros en 12 días ¿cuánto se demorarían 9 obreros, trabajando en igualdad de condiciones?

8. En una bodega hay comida para 50 personas durante un mes, ¿cuántos días podrían comer 80 personas?

9. En una pastelería se venden tortas selva negra y tortas de piña. Si la razón entre el número de tortas selva negra y de piña vendidas en un día es de 3 a 4 ¿cuántas tortas de piña se vendieron en un día, si de selva negra se vendieron 30 unidades?

10. Complete los datos en cada tabla y clasifica estas según sean variaciones directamente proporcionales, inversamente proporcionales o de proporcionalidad compuesta.

a. Gastos de comida diarios por cada cinco competidores:

b. Número de buses, de igual capacidad que se necesita contratar para transportar a 300 deportistas:

11. Margarita quiere hacer un postre de chocolate para su fiesta de cumpleaños. Para ello, consulta un libro de cocina y la receta indica que para 6 personas hay que utilizar 120 gramos de chocolate, ¿qué cantidad de chocolate tendrá que usar si a la fiesta van 12 personas?, ¿y si van 18?, ¿y para tres personas?

Escriba los datos en una tabla:

12. En la siguiente tabla de valores se registran las temperaturas desde las 18 horas de un día hasta las 12 del día siguiente:

a. Realice un gráfico que relacione tiempo (en el eje horizontal) con temperatura (en el eje vertical).

b. Analice las características del gráfico respecto del aumento o de la disminución de la temperatura.

c. Realice una estimación de la temperatura promedio: en las horas observadas y también entre las 22:00 y las 06:00 horas.

d. ¿En qué intervalo o intervalos se produce la mayor disminución de temperatura?, ¿en cuál la menor disminución?, ¿en cuál el mayor aumento?

e. ¿En qué intervalos se produce la máxima o la mínima temperatura?

13. En una biblioteca se colocan 2610 libros en dos muebles de 40 y 50 estanterías cada uno, ¿cuántos libros se colocarán en cada mueble si se reparten proporcionalmente al número de estantes de cada uno?

14. El guía del campamento de los cursos A, B y C de 3º de Secundaria les ha dado a los alumnos una bolsa de etiquetas para identificar las plantas. Si la bolsa tiene 624 etiquetas y los cursos tienen 11, 13 y 15 alumnos, respectivamente, ¿cuántas le tocan a cada uno si cada alumno debe recibir la misma cantidad?, ¿y a cada grupo?

15. Tres jugadores de fútbol se reparten 36 000 euros en proporción directa al número de partidos que ha jugado cada uno. Si jugaron 12, 15 y 18 respectivamente, ¿cómo se repartirán el dinero?

16. Se quieren repartir 396 m 2de un terreno entre tres familias, de forma directamente proporcional al número de hijos de cada una. Si cada familia tiene 2, 4 y 5 hijos respectivamente, ¿qué parte del terreno recibirá cada una?

17. Si al distribuir cierta cantidad de dinero entre 6 personas cada uno recibe 20 euros ¿cuánto recibirán si se repartiese entre 15 personas?, ¿cuál es la constante de proporcionalidad inversa?

18. Con el agua de un depósito se llenan 630 botellas de 3/4 de litro, ¿cuántas botellas de 3/2 se necesitarán para almacenar la misma cantidad de agua?