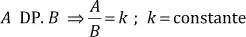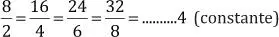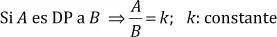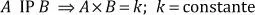Juan Egoavil Vera - Fundamentos de matemática

PROPORCIONALIDAD INTERACTIVA (2014) ( http://proporcionalidadinteractiva.blogspot.com/2012/10/normal-0-21-false-false-false-es-co-x_197.html) Blog dedicado a profundizar los conceptos relacionados con la proporcionalidad (Consulta: 20 de enero)

Objetivos

• Diferenciar las características que poseen las magnitudes según su naturaleza.

• Obtener conclusiones acerca de las relaciones que cumplen determinadas magnitudes que participan en casos particulares.

• Establecer una relación de las magnitudes con nuestra realidad cotidiana para un adecuado planteamiento de la resolución de un problema.

Introducción

La proporcionalidad numérica es un concepto que resulta a los alumnos complejo y difícil de comprender si no se ha adquirido soltura en aspectos como las operaciones de multiplicación y división de números enteros y por la unidad seguida de ceros, la equivalencia de fracciones, la fracción como expresión decimal y de una cantidad y el porcentaje.

A través de la comprensión de los conceptos de magnitud, proporción, razón y constante de proporcionalidad se aplican las proporciones y sus métodos de resolución de problemas a situaciones de la vida cotidiana.

Las relaciones entre magnitudes inversamente proporcionales plantean un mayor grado de dificultad y se estudiarán mediante relaciones entre proporciones.

Concepto de Magnitud

• Una magnitud es una cualidad o una característica de un objeto que podemos medir. Ejemplo: longitud, masa, número de alumnos, capacidad, velocidad, etcétera.

• Las magnitudes se expresan en unidades de medida.

Ejemplo: metros, kilómetros, kilogramos, gramos, número de personas, litros, centilitros, kilómetros por hora, metros por segundo, etcétera.

• Para cada una de esas medidas existen diferentes cantidades de esa magnitud.

Ejemplo: una regla de 1 metro, una caja de 2 kilogramos, un tonel de 5 litros, 95 km/h, etcétera.

Actividad 1.15:

1. Indique con una « » si los siguientes enunciados son magnitudes.

a. El peso de un saco de patatas.

( )

b. El cariño.

( )

c. Las dimensiones de tu carpeta.

( )

d. La belleza.

( )

e. Los litros de agua de una piscina.

( )

f. La risa.

( )

2. Indique dos unidades de medida para cada magnitud.

a. El precio de una bicicleta.

b. La distancia entre dos pueblos.

c. El peso de una bolsa de naranjas.

d. El contenido de una botella.

e. El agua de un embalse.

f. La longitud de la banda de un campo de fútbol.

Relación entre magnitudes

Las relaciones matemáticas que existen entre las magnitudes son de mucha importancia, ya que nos permiten deducir la variación de una magnitud, modificando los valores de las magnitudes con los que está en interdependencia, considerando que estas relaciones pueden ser sencillas (solo entre dos magnitudes) y otras más complejas (más de dos magnitudes). A continuación estudiaremos las dos magnitudes.

Magnitudes directamente proporcionales (DP)

Dos magnitudes son directamente proporcionales, si al aumentar o disminuir una de ellas, entonces la otra aumenta o disminuye en las mismas proporciones.

Notación:

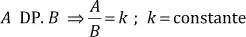
Ejemplo:

Observe que si duplicamos el n.° de huevos, el costo también se duplicará. Ocurrirá lo mismo si triplicamos, cuadriplicamos, etcétera.

Se cumple:

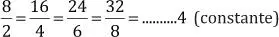
Se concluye que: «Si dos magnitudes ( A y B ) son directamente proporcionales, el cociente de sus valores correspondientes es una constante, llamada constante de proporcionalidad».

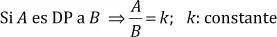
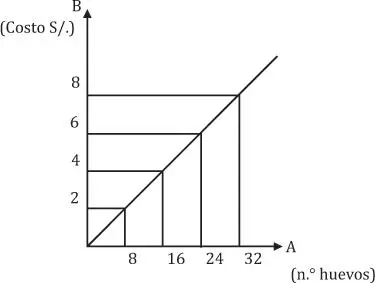
Graficando el ejemplo planteado al principio, observaremos que se trata de una recta, en efecto:

Actividad 1.16:

1. Indique con un « » si las siguientes magnitudes son directamente proporcionales.

a. El peso de naranjas (en kilogramos) y su precio.

( )

b. La velocidad de un auto y el tiempo que emplea en recorrer una distancia.

( )

c. El número de operarios de una obra y el tiempo que tardan en terminarla.

( )

d. El número de hojas de un libro y su peso.

( )

e. El precio de una tela y cuántos metros se van a comprar.

( )

f. La edad de un alumno y su altura.

( )

2. Un túnel de lavado limpia 12 autos en una hora (60 minutos) ¿cuánto tiempo tardará en lavar 25 autos?, ¿y 50?

Magnitudes inversamente proporcionales (IP)

Dos magnitudes son inversamente proporcionales, si al aumentar o disminuir una de ellas, entonces la otra disminuye o aumenta en proporciones inversas.

Notación:

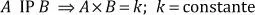
Ejemplo:

Observe que si duplicamos el n.° de obreros, el n.° de días se reduce a la mitad. Ocurrirá lo mismo si triplicamos, cuadruplicamos, etcétera.

Se cumple:

2×24 = 4×12 = 6×8 = … = 48 (constante)

Se concluye que: «Si dos magnitudes ( A y B ) son inversamente proporcionales, el producto de sus valores correspondientes es una constante, llamada constante de proporcionalidad».

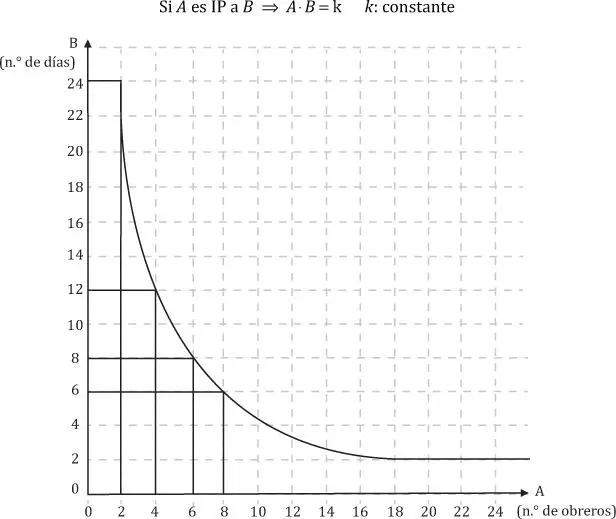
Graficando el ejemplo planteado líneas arriba, observamos que se trata de una hipérbola.

Actividad 1.17:

1. Indique con un « » si las siguientes magnitudes son inversamente proporcionales.

a. La velocidad de un auto y el tiempo que tarda en recorrer una distancia.

( )

b. El número de limpiadores de un edificio y el tiempo que tardan.

( )

c. El número de ladrillos de una pared y su altura.

( )

d. El peso de la fruta y el dinero que cuesta.

( )

e. La velocidad de un corredor y la distancia que recorre.

( )

f. El número de grifos de un depósito y el tiempo que tarda en llenarse.