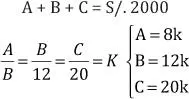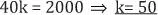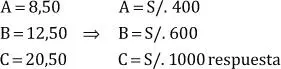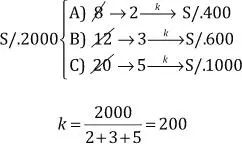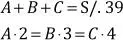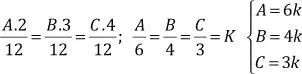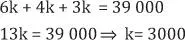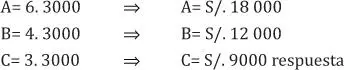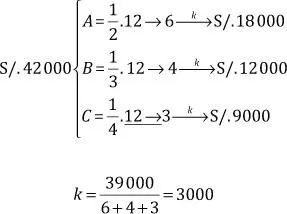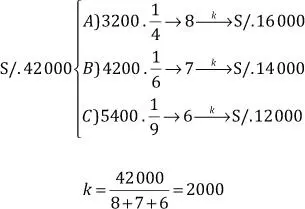Juan Egoavil Vera - Fundamentos de matemática

( )

2. Un depósito de agua se llena en 18 horas con un grifo del que salen 360 litros de agua cada minuto.

a. ¿Cuánto tardaría en llenarse el depósito si salieran 270 litros por minuto?

b. ¿Y si fueran 630 litros por minuto?

Reparto proporcional

Es un procedimiento que tiene como objetivo dividir una cantidad en partes que sean proporcionales a ciertos valores, llamados índices.

Clases:

1. Reparto simple: se llama así porque intervienen solo dos magnitudes proporcionales. Puede ser:

1.1. Directo : (cuando intervienen 2 magnitudes DP)

Analicemos el siguiente caso: un padre quiere repartir S/. 2000 entre sus tres hijos, cuyas edades son 8, 12 y 20 años. El padre piensa, con justa razón, que su hijo de 20 años tiene mayores necesidades económicas que su otro hijo de 8 años, entonces decide hacer el reparto DP a las edades de sus hijos. Esto implica que aquel hijo que tenga más edad, recibirá más dinero, y el que tenga menos edad, recibirá menos dinero. Veamos lo que sucede.

Sean las partes A, B y C, tales que cumplen las siguientes condiciones:

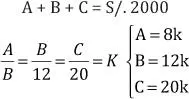
Recuerde que cuando dos magnitudes son DP el cociente entre ellas es una constante.

Entonces: 8k + 12l + 20k = 2000

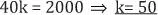
Luego c/u le responde:

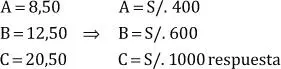
Podemos resolver el problema mediante el siguiente esquema práctico:

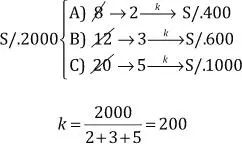
Observe que si simplificamos los tres números, la relación de proporcionalidad no se altera. Luego, la constante de reparto «k» se halla dividiendo la cantidad a repartir (S/. 2000) entre la suma de las partes (2,3 y 5). Finalmente, las cantidades recibidas por c/u se hallan multiplicando 2, 3 y 5 por k.

Actividad 1.18:

María, Pablo y Luisa se proponen vender 600 boletos de una rifa con el fin de recaudar fondos para rehabilitar la Casa de la Cultura de su pueblo. Se las reparten proporcionalmente a 3, 4 y 5, respectivamente ¿cuántos boletos debe vender cada uno?

1.2. Inverso: (cuando intervienen 2 magnitudes IP)

Analicemos el siguiente caso: un administrador quiere compensar a sus tres mejores empleados dándoles una gratificación por sus altos rendimientos. El problema es que los tres empleados tienen algunas faltas y desea que esa situación se vea reflejada en el reparto. Entonces, plantea repartir los S/. 39 000 en partes IP a sus faltas, que son 2, 3 y 4 días respectivamente. Esto implica que aquel empleado que tenga más faltas, recibirá menos dinero, mientras que el que tenga menos faltas recibirá más dinero. Veamos qué sucede.

Sean las partes A, B y C, tales que cumplen las siguientes condiciones:

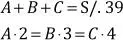
Entonces, dividiendo la última expresión entre 12

(MCM (2; 3; 4)= 12):

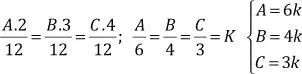
Recuerde que cuando dos magnitudes son IP el producto entre ellas es una constante.

Luego:

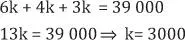
A c/u le corresponde:

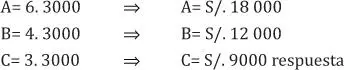
Podemos resolver el problema empleando el método práctico, planteado en el caso anterior:

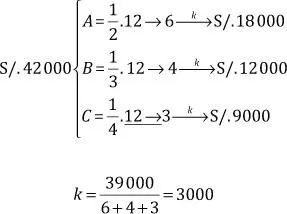
No olvide: MCM (2,3,4) = 12

Observe que los números que representan las faltas de estos tres empleados se colocan invertidos (recuerde que el reparto es IP), luego si a cada uno de ellos se les multiplica por 12, la relación de proporcionalidad no se altera. Lo que se realiza a continuación es lo mismo que se ha descrito en el reparto anterior (reparto directo).

Actividad 1.19:

Adela quiere repartir S/. 2100 entre sus sobrinos Javier, Elena y Pablo, de manera inversamente proporcional a la edad de cada uno. Javier tiene 3 años, Elena 5 y Pablo 6 años ¿qué cantidad recibirá cada uno?

2. Reparto compuesto: se llama así porque intervienen más de dos magnitudes proporcionales.

Ejemplo:

Un gerente desea repartir una gratificación de S/. 42 000 entre sus tres empleados en partes DP a sus sueldos (S/. 3200, S/. 4200 y S/. 5400) e IP a sus faltas (4, 6 y 9 días, respectivamente) ¿cuánto le corresponde a cada uno?

Solución:

Resolveremos el problema utilizando el método práctico:

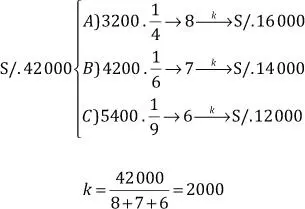
Observe que a pesar que el tercer empleado gana más (S/. 5400) no es él quien recibe más gratificación. Esto se debe a que sus faltas (9 días) son muchas, causando una disminución en la gratificación que recibió.

Trabajemos en clase

1. Compruebe si los siguientes números forman una proporción:

• 1, 30, 140 y 200.

• 16, 25, 14 y 21.

2. Un auto consume 5 galones de gasolina cada 100 km. Si quedan en el depósito 6 galones, ¿cuántos kilómetros podrá recorrer el coche?

3. Si 3 hombres necesitan 24 días para hacer un trabajo ¿cuántos días emplearán 18 hombres para realizar el mismo trabajo?

4. Para colaborar en el viaje de fin de curso, una institución educativa reparte S/. 1800 entre las tres secciones de quinto de secundaria de manera proporcional al número de alumnos de cada sección: 24, 30 y 36 respectivamente ¿qué cantidad recibirá cada sección?

5. En un concurso de preguntas y respuestas, se reparte un premio de S/. 2310 de manera inversamente proporcional al tiempo que se han tardado en responder correctamente los tres primeros clasificados (5, 10 y 15 minutos respectivamente), ¿qué cantidad le corresponde a cada uno?

Ejercicios y problemas

Manejo de conceptos

1. Indique si las siguientes afirmaciones son verdaderas o falsas.

a. Dos magnitudes son directamente proporcionales cuando una de ellas aumenta al doble, la otra también aumenta el doble.

( )

b. La cantidad de panes que como y lo que gasto comiendo es inversamente proporcional.