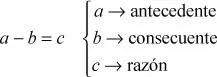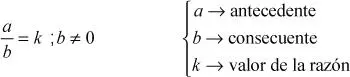9. En un colegio se eligió la reina que los representaría.  de los alumnos votaron a la candidata número 1,
de los alumnos votaron a la candidata número 1, 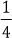 a la candidata número 7 y 187 alumnos votaron por otras ¿cuántos alumnos votaron?
a la candidata número 7 y 187 alumnos votaron por otras ¿cuántos alumnos votaron?
10. El perímetro de un triángulo isósceles es igual a 39 cm. Si cada uno de los lados congruentes es igual a los  de la base, ¿cuál es la longitud de cada lado?
de la base, ¿cuál es la longitud de cada lado?
11. Durante la primera hora, el dueño de un quiosco de periódicos vendió la cuarta parte de los diarios que tenía, en la segunda hora la sexta parte de lo que quedaba. Contó los ejemplares y le quedaban 25 ¿cuántos diarios tuvo en total?
12. Un avión está dividido en tres categorías de pasajeros: primera clase tiene un octavo del total de asientos, categoría ejecutivo tiene una vez y media de los asientos de primera clase y hay 165 asientos de turistas ¿cuántos asientos tiene el avión?, ¿cuántos asientos de cada clase hay?

Páginas web para consultar
| Ejemplos, ejercicios y juegos de fracciones: |
| http://www2.gobiernodecanarias.org/educacion/17/WebC/eltanque/todo_mate/fracciones_e/fracciones_ej_p.html |
 |
| http://www.vedoque.com/juegos/matematicas-04-fracciones.swf |
 |
El hombre de Vitruvio
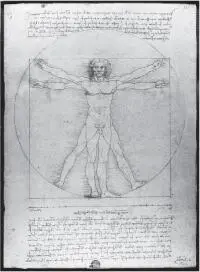
Leonardo Da Vinci realizó un dibujo llamado «El hombre de Vitruvio» en un diario suyo en el cual representaba a la figura humana vista en dos posiciones sobreimpresas y que está basado en las proporciones del cuerpo humano, es llamado Vitruvio pero con leves desviaciones. Este dibujo está inscrito en un cuadrado de donde sus diagonales se cruzan en los genitales y una circunferencia en la cual el centro se halla en el ombligo del dibujo, pero en la realidad, como media está desplazada ligeramente hacia arriba. El cuadrado y la circunferencia representan al hombre como centro de todas las cosas y es uno de los grandes logros del renacimiento, debido al descubrimiento de las proporciones matemáticas que están aplicadas al dibujo que está hecho en lápiz y tinta, y mide 34,2 x 24,5 cm. Da Vinci realizó este dibujo representando las proporciones del cuerpo humano y, analizando el dibujo en todo su contenido, se descifra que:
Una palma equivale al ancho de cuatro dedos.
Un pie equivale al ancho de cuatro palmas.
Un antebrazo equivale al ancho de seis palmas.
La altura de un hombre son cuatro antebrazos.
Un paso es igual a un antebrazo.
La longitud de los brazos extendidos es igual a su altura.
La distancia entre el nacimiento del pelo y la barbilla es un décimo de la altura de un hombre.
La altura de la cabeza hasta la barbilla es un octavo de la altura de un hombre.
La distancia entre el nacimiento del pelo a la parte superior del pecho es un séptimo de la altura de un hombre.
La altura de la cabeza hasta el final de las costillas es un cuarto de la altura de un hombre.
La anchura máxima de los hombros es un cuarto de la altura de un hombre.
La distancia del codo al extremo de la mano es un quinto de la altura de un hombre.
La distancia del codo a la axila es un octavo de la altura de un hombre.
La longitud de la mano es un décimo de la altura de un hombre.
La distancia de la barbilla a la nariz es un tercio de la longitud de la cara.
La distancia entre el nacimiento del pelo y las cejas es un tercio de la longitud de la cara.
La altura de la oreja es un tercio de la longitud de la cara.
La distancia desde la planta del pie hasta debajo de la rodilla es la cuarta parte del hombre.
La distancia desde debajo de la rodilla hasta el inicio de los genitales es la cuarta parte del hombre.
CHAVES PINTOS, Pablo. (2009) Leonardo Da Vinci. (Consulta: 11 de marzo de 2013). ( http://centros.edu.xunta.es/iesramoncabanillas/cuadmat/trabaj/brazo5.pdf)
Objetivos
• Representar simbólicamente razones y proporciones y distinguir sus propiedades.
• Reconocer las diferencias entre magnitudes directamente proporcionales y magnitudes inversamente proporcionales.
• Matematizar situaciones concretas y resolver problemas aplicando las propiedades de las magnitudes directas e inversamente proporcionales.
Razones
La razón consiste en comparar dos cantidades cualesquiera para poder establecer una característica que las relacione, en particular ambas cantidades las podemos comparar principalmente de dos formas: a través de su diferencia (razón aritmética), y mediante su cociente (razón geométrica):
a. Razón Aritmética: es una forma de comparar dos cantidades en las cuales consideramos cuánto excede una de la otra, es decir, encontrando su diferencia.
Este tipo de razón la podemos escribir separando ambas cantidades por comparar con un signo menos (–). Así, la razón aritmética entre un par de números a y b , es: a – b , y se lee a es a b . El primer término de una razón aritmética se denomina antecedente, mientras que el segundo consecuente. antecedente consecuente
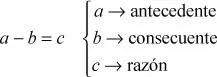
Actividad 1.13:
Un padre quiere repartir unos ahorros a sus dos hijos, pero al fin del mes uno de ellos se portó mal, por lo cual lo castigará dándole S/. 6000 menos que a su hermano. Si dispone de S/. 20 000 para repartir ¿cuánto le corresponde a cada uno?
b. Razón Geométrica: cada vez que se habla de razón en realidad se quiere hacer referencia a una razón geométrica.
La razón geométrica entre dos cantidades a y b es la comparación por cociente entre ambas, es decir, la división entre ellas. Este tipo de razón la podemos representar de dos formas: a través de un signo de división (÷ o:) o expresada en forma fraccionaria. De ambas formas se lee a es a b . Al igual que la razón aritmética el primer término se denomina antecedente, y el segundo, consecuente.
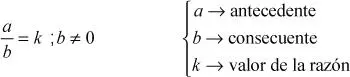
El tratamiento de las razones geométricas es similar al de las fracciones, es decir, se suman, restan, multiplican, dividen, simplifican y amplifican de la misma forma.
Ahora ¿a qué nos referimos específicamente cuando decimos 3 es a 5?, por ejemplo. La respuesta es muy sencilla: quiere decir que cada vez que tengamos 3 partes del antecedente tendremos 5 del consecuente, y en conjunto formamos 8 partes.
Читать дальше

 de los alumnos votaron a la candidata número 1,
de los alumnos votaron a la candidata número 1, 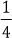 a la candidata número 7 y 187 alumnos votaron por otras ¿cuántos alumnos votaron?
a la candidata número 7 y 187 alumnos votaron por otras ¿cuántos alumnos votaron? de la base, ¿cuál es la longitud de cada lado?
de la base, ¿cuál es la longitud de cada lado?