Actividad 1.14:
a. Al siguiente mes, el mismo padre (actividad anterior) tiene el mismo problema, uno de sus hijos se ha portado mal, por lo que quiere darle menos dinero que a su hermano, pero esta vez quiere que por cada S/. 3000 del hermano que se portó bien, el otro reciba solo S/. 2000, es decir quiere repartir el dinero a razón de 3 es a 2. Si dispone nuevamente de S/. 20 000, ¿cuánto dinero le corresponderá a cada uno?
b. Los ángulos de un triángulo están a razón de 1: 2 : 3 (recuerda que esto se lee; uno es a dos es a tres), sabiendo que la suma de los ángulos interiores de un triángulo es 180 grados ¿cuánto miden sus ángulos?
Proporciones
Una proporción es una igualdad entre dos razones equivalentes.
a. Proporción Aritmética o Equidiferencia: es la igualación de dos razones aritméticas equivalentes. A la diferencia entre las razones involucradas se la llama constante de proporcionalidad aritmética.
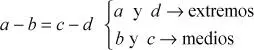
Propiedad fundamental:
«En toda proporción aritmética la suma de los extremos es igual a la suma de los medios»

Ejemplo: 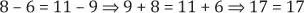
b. Proporción Geométrica o Equicocientes: una proporción geométrica (o simplemente proporción), es la igualación de dos razones geométricas equivalentes. En una proporción podemos distinguir sus partes por distintos nombres, están los extremos que son el antecedente de la primera razón y el consecuente de la segunda, y los medios, que son el consecuente de la primera razón y el antecedente de la segunda.
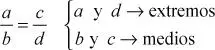
Propiedad fundamental:
«En toda proporción geométrica, el producto de los extremos es igual al producto de los medios»
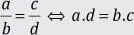
Una proporción es continua cuando los medios de la proporción son iguales
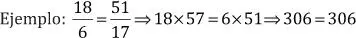
Propiedades de las Proporciones Geométricas
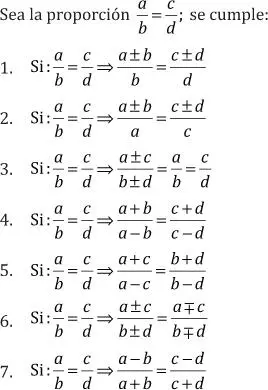

Trabajemos en clase
1. Aplicando la propiedad fundamental de las proporciones, calcule el valor de x :

2. Aplique las propiedades de las proporciones para resolver las siguientes situaciones matemáticas:
a. La suma entre dos números es igual a 175 y la razón entre ellos es 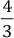 ¿cuáles son los números que cumplen las condiciones?
¿cuáles son los números que cumplen las condiciones?
b. La diferencia entre el dinero que tiene Juan y el que tiene Gustavo es de $ 400. La cantidad de dinero de Juan es a la de Gustavo como 9 es a 7 ¿cuánto dinero tiene cada uno?
c. La suma entre dos números es igual a 10,5 y la razón entre ellos es  ¿cuáles son los números?
¿cuáles son los números?
d. Un veterinario sabe que la ración diaria de alimento para un perro bóxer y un pequinés es de 2 kg. El perro bóxer come tres veces más alimento que el pequinés ¿qué cantidad de alimento consume cada perro?
e. Pruebe su ingenio y calcule los valores de a, b, c y d :
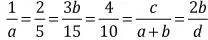

Ejercicios y problemas
Manejo de conceptos
1. Analice la proporción 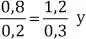 luego indique si las siguientes afirmaciones son verdaderas o falsas.
luego indique si las siguientes afirmaciones son verdaderas o falsas.
a. La razón de la proporción es 4.
( )
b. 0,8 y 0,3 son los términos extremos.
( )
c. 0,2 y 0,3 son los términos medios.
( )
d. El producto de los términos medios es 0,25.
( )
e. El producto de los términos extremos es 0,24.
( )
f. La suma de los antecedentes entre la suma de los consecuentes es igual a la razón de proporcionalidad.
( )
g. Si 0,8 ×... = ...× 1,2; la suma de los términos que faltan es 0,5.
( )
2. En cada enunciado marque la alternativa correcta:
2.1 Podemos afirmar que una razón es:
a. La comparación de dos cantidades por cociente.
b. El producto de dos cantidades dadas.
c. La suma de dos cantidades.
d. La relación entre dos cantidades.
e. La igualdad entre dos cantidades.
2.2 Una proporción es:
a. La igualdad de dos cantidades.
b. El producto de dos razones.
c. El cociente entre dos razones.
d. La igualdad de dos razones.
e. La suma de dos razones.
2.3 Diremos que una proporción es directa si:
a. Al aumentar uno de sus valores el otro disminuye.
b. Al disminuir una de las cantidades la otra aumenta.
c. El producto de las cantidades se mantiene constante.
d. Al aumentar una de las cantidades la otra también lo hace.
e. Ninguna de las anteriores.
2.4 En una proporción inversa se mantiene constante:
a. El cociente de las cantidades relacionadas.
b. El producto de las cantidades relacionadas.
c. La suma de las cantidades relacionadas.
d. La diferencia de las cantidades relacionadas.
e. Ninguna de las anteriores.
Habilidades de cálculo
1. Dos números son entre sí como 7 es a 13, si al menor se le suma 140, para que el valor de la razón no se altere, el valor del otro número debe quintuplicarse. Halle el valor de los dos números.
2. Dos números son entre sí como 5 a 8, si la suma de sus cuadrados es 712 ¿cuál es el número menor?
3. La suma, la diferencia y el producto de dos números están en la misma relación con los números 11; 3 y 560. Halle el mayor de los números.
4. En una proporción continua geométrica los términos extremos son entre sí como 4 es a 9. Si los términos de la primera razón suman 40 halle la suma de los consecuentes de dicha proporción.
5. En una proporción geométrica discreta la diferencia entre los medios es 14. Halle uno de los términos medios si se sabe que el producto de los cuatro términos de la proporción es 2601.
Читать дальше

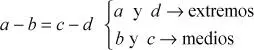

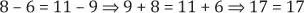
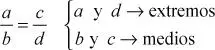
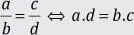
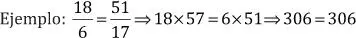
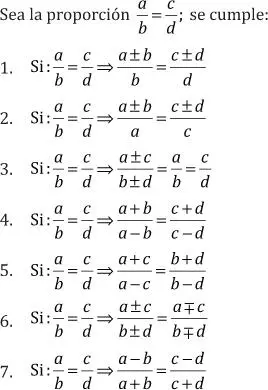


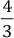 ¿cuáles son los números que cumplen las condiciones?
¿cuáles son los números que cumplen las condiciones? ¿cuáles son los números?
¿cuáles son los números?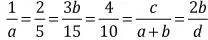

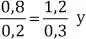 luego indique si las siguientes afirmaciones son verdaderas o falsas.
luego indique si las siguientes afirmaciones son verdaderas o falsas.










