Markus Falk - Die Impfdebatte

Um es vorweg zu nehmen: Die Inokulation war problematisch und sie verbreitete sich in Europa nur allmählich (Italien und Frankreich um 1750, Schweden um 1760, Deutschland/Österreich und Russland um 1770). Zeitweise gab es auch Inokulationsverbote wie beispielsweise 1763 in Paris, da bei einem Pockenausbruch im Winter 1762/63 nicht klar war, ob diese auf die Inokulation zurück ging.

Auch wenn in Frankreich kaum inokuliert wurde, so wurde umso mehr darüber gestritten. Befürworter der Inokulation hatten vielfach in England darüber erfahren und diese miterlebt, waren oft selbst als Kind oder Erwachsener erkrankt und hatten so am eigenen Leibe erfahren, was die Pocken bedeuteten.

Sie waren der Meinung, man dürfe sich dem medizinischen Fortschritt nicht verschließen und versuchten fast schon missionsartig den Inokulationsgedanken zu verbreiten. Zu diesen zählten Persönlichkeiten wie Voltaire, bedeutender französischer Philosoph und Wegbereiter der französischen Revolution, sowie Diderot, Herausgeber der französischen Encyclopédie, eine der ersten Enzyklopädien im heutigen Sinne und Hauptwerk der Aufklärung. Im deutschen Sprachraum kam diese Rolle Goethe zuteil und in Österreich war es Maria Theresia, die sich für die Inokulation stark machte. Größte Gegner waren zum einen hochrangige Ärzte, wie der Dekan der medizinischen Fakultät in Paris, Theologen und ganz normale Bürger, die in der Inokulation vor allem die Gefahren sahen. Einer der Höhepunkte der Inokulationsdebatte war wohl der Disput zwischen Daniel Bernoulli (schweizer Mathematiker/Physiker und studierter Arzt) und d’Alembert (französischer Mathematiker/Physiker und Mitherausgeber genannter Encyclopédie).

Bernoulli und d’Alembert lagen im Wettstreit miteinander. Beide galten als herausragende Mathematiker und beide waren mit der Lösung der Wellengleichung schwingender Saiten befasst. Es war d’Alembert, der als Erster (1747) die Lösung in Form von Differentialgleichungen fand und somit schneller als Bernoulli war. Dies ist hier inhaltlich wenig von Bedeutung, macht aber die später zwischen den beiden sehr hart geführte Debatte verständlicher, als dass sich Bernoulli als Impfbefürworter diesmal bei den Gewinnern sah.

2.2.1. Der Disput zwischen Bernoulli und d’Alembert (1760 – 1766)

Die Franzosen verfügten zwar über keine Daten, holten sich diese aber von den Engländern, und gar einige Mathematiker versuchten sich an der Berechnung der Pockensterblichkeit in Abhängigkeit von der Inokulation. Bernoulli präsentierte als Erster eine Lösung (1760) und er ermittelte für nicht Inokulierte ein um 25-mal höheres Sterberisiko als für jene, die sich inokulieren ließen (Sterberisiko durch Inokulation 1 auf 200). Hiermit verbunden war ein Zugewinn von 2 Jahren und 2 Monate an durchschnittlicher Lebenszeit unter Berücksichtigung anderer Todesursachen, alles jeweils berechnet ab Geburt. Sein Modell (Kompartiment Modell mittels Differentialgleichungen aufgelöst) war gänzlich neu und dieses wird heute noch in der Pharmakokinetik verwendet. Bernoulli sah in seinen Ergebnissen die Bestätigung, dass eine Inokulation nicht nur für den Einzelnen gut sei, sondern vor allem auch für den Staat, da damit die damals niedrige Lebenserwartung von ca. 27 Jahren auf etwa 30 erhöht werden könnte. Die Aufklärung änderte nicht nur den Stellenwert des Einzelnen, sondern Staaten erkannten zunehmend den Wert von Humanressourcen und die Befürworter der Inokulation waren regelrecht begeistert. Aus Bernoullis Berechnungen folgte auch, dass es sowas wie eine Herdenimmunität geben müsste, d.h. dass durch die zunehmende Anzahl Immunisierter die Ausbreitung der Erkrankung eingedämmt werden kann. Der Gedanken an die Ausrottung einer Krankheit lag somit nahe. Bernoulli ging sogar so weit, als dass er zeigte, dass selbst unter Annahme einer hohen Opferzahl unter den Inokulierten (11% versterben an der Inokulation) der Vorteil dieser immer noch überwog und eine Inokulationspflicht deshalb gerechtfertigt sein könnte ( Abbildung 5). Bernoulli begründete damit auch die Grundauslegung des heutigen Impfcredos.

Obwohl d’Alemebert der Inokulation gegenüber aufgeschlossen war, hegte er starke Zweifel und seine Replik ließ nicht lange auf sich warten. Bereits ein halbes Jahr später trug er seine Erkenntnisse vor und publizierte diese 1761. Bernoulli brauchte hierfür wesentlich länger, arbeitete auch d’Alemberts Kritik mit ein und sein Artikel erschien erst 1766. D‘Alembert war auch klar, welche Verantwortung er trug und er war darauf bedacht, dass seine Kritik an der Inokulation nicht von Gegnern missbraucht würde. Ihm lag also viel an einer Vernunftsdiskussion und er wollte sich nicht in den Glaubenskrieg hineinziehen lassen. Es war vermutlich auch die Rivalität zu Bernoulli, die ihn dazu veranlasste Bernoullis Lösung stark in Abrede zu stellen. Wir er selbst an der Wellgleichung gezeigt hatte, lassen sich physikalische Probleme mittels Differentialgleichungen lösen. Ein ähnlicher Ansatz zur Modellierung von Erkrankungen mag zwar mathematisch korrekt gefasst sein, anhand welcher Daten soll dies aber überprüfbar sein? Sein größter Kritikpunkt war deshalb die Güte der verwendeten Parameterwerte und er meinte ein Modell möge auch noch so ausgefeilt sein, wenn die Parameterwerte nicht stimmen, dann wären die Ergebnisse wertlos. Er schlug deshalb einen alternativen Ansatz vor, der wesentlich weniger Annahmen benötigte. Man würde diesen heute als nicht-parametrisches Verfahren bezeichnen, wie wir es in modernen Überlebenszeitanalysen ebenfalls wiederfinden.

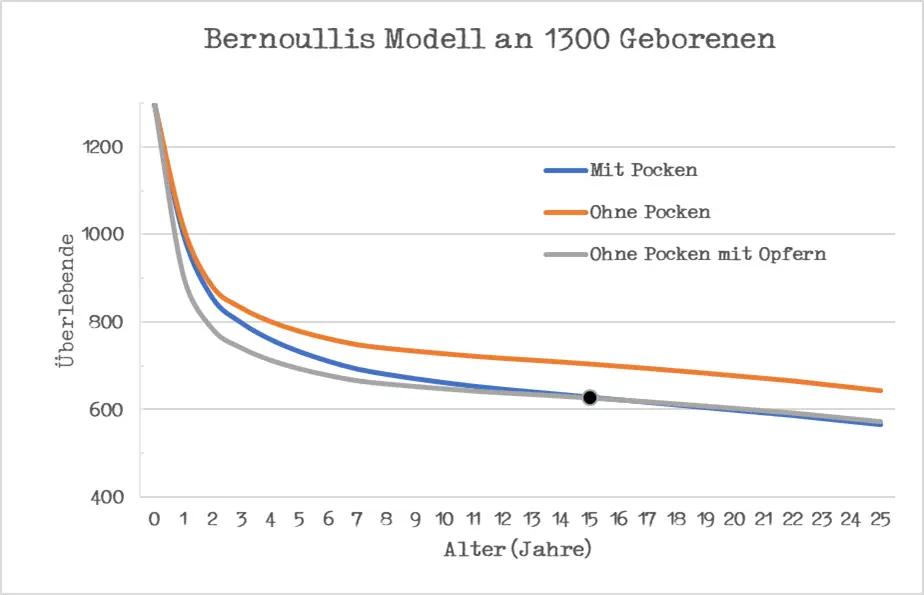
Abbildung 5: Bernoullis Schätzung für den Zugewinn an Überlebenszeit, dargestellt an 1300 Geborenen. Die blaue Linie zeigt die Situation bei zirkulierenden Pocken. Von 1300 Geborenen würden im Alter von 25 Jahren noch 565 am Leben sein. Angenommen man würde die Pocken ausrotten (rote Linie), dann wären im Alter von 25 Jahren noch 644 und somit 79 Personen oder 14% mehr am Leben. Selbst unter der Annahme, dass an der Inokulation 11% versterben würden (graue Linie) und dies ist übertrieben hoch angesetzt, wäre schlussendlich immer noch ein Zugewinn von 8 Personen zu verzeichnen, da sich die Situation ab dem Alter von 15 Jahren zu Gunsten der Inokulation verschiebt.

D’Alembert kam ebenfalls zum Schluss, dass die Inokulation von Vorteil sei. Er setzte jedoch voraus, dass sie möglichst ungefährlich sein müsse, dass man lebenslang geschützt bliebe und dass keine andere Todesursache diesen Vorteil wieder wett machen könne. D’Alembert zog aus dieser Erkenntnis jedoch ganz andere Schlüsse als Bernoulli. Für ihn stand das persönliche Risiko im Vordergrund und er meinte: „Was, wenn ich dieser eine Geschädigte auf 200 Inokulierte bin?“. Für ihn war klar, jeder, der sich inokulieren lässt, hat seine Gründe hierfür gefunden. Dies kann die Angst vor der Erkrankung sein, der Schutz der eigenen Kinder oder der Wunsch die Schönheit zu erhalten (Frauen und Pockennarben). Umgekehrt kann er aber auch verstehen, dass man von der Inokulation Abstand nimmt, da man Angst hat sein Kind oder sein Leben zu verlieren, obwohl es sonst noch angehalten hätte. Man soll deshalb weder zur Inokulation aufrufen oder jemanden dazu drängen, noch davon abhalten und es müsse jedem selbst die Entscheidung überlassen werden. Kant drückte etwas ganz Ähnliches in einer Notiz zur Pockennot 40 Jahre später aus [36]: „Verdamnis all jenen die Jemanden in die eine oder andere Gefahr bringen, mit oder ohne Einwilligung, damit etwas Gutes herauskomme, das ohne diese Gefährdung nicht erreicht würde.“

D’Alembert ging in seiner Replik zu Bernoulli noch weiter. Bernoullis Berechnungen zeigten, dass selbst bei einer hohen Opferzahl durch die Inokulation auf lange Sicht mehr Personen überlebten. Die Inokulation musste hierfür einfach weniger letal als die Erkrankung selbst sein (Bernoulli nahm eine Letalität von 12,5% für Pocken an). Für d’Alembert war aber der Gedanke viele sofort zu opfern, um später davon zu profitieren nicht begründbar und somit unhaltbar. Wie soll sich jemand entscheiden können, wenn er nur die Möglichkeiten hat entweder gleich durch die Inokulation zu versterben oder später durch die Erkrankung selbst? Das lebensnahe Ereignis würde doch von jedem als riskanter beurteilt werden als das ferne Ereignis. Er war deshalb gänzlich dagegen, dass der Staat über die Interessen des Individuums hinweg entscheide. Ebenso wenig war er für die Einschränkung der Inokulation durch Staaten oder Fachkreise, da der mögliche Nutzen für alle durchaus gerechtfertigt sei. Er schlug eine Art Ehrenauszeichnung für Inokulations-Geschädigte vor, da sich diese ja auch für andere opferten. Seine Überlegungen stellte er an zahlreichen Beispielen dar und verwendete hierfür auch das von Bernoulli Jahre zuvor formulierte St.-Petersburg-Paradoxon. Dieses war ein heiß diskutiertes Problem der damaligen Zeit und es war damals Mode die Wahrscheinlichkeitsrechnung für alle möglichen Belange heranzuziehen. Für eine Lösung gab es teilweise hohe Preisgelder, denn man war gerade dabei genauer zu verstehen, was es mit Wahrscheinlichkeiten so auf sich hatte. Beim St.-Petersburg-Paradoxon ging es nicht um die eigentliche Lösung, sondern vielmehr um die Erkenntnisse, die man daraus zu ziehen hätte. Das Paradoxon bestand darin, dass man nicht abschätzen konnte wie groß die Risikobereitschaft war an einem Glücksspiel teilzunehmen, bei dem ein unendlich hoher Gewinn wie auch Verlust zu erwarten war. Bei dem Spiel wird eine Münze geworfen. Kommt Kopf im ersten Wurf erhält man 2 Euro. Kommt Kopf erst beim Zweiten, dann erhält man 4, beim Dritten 8 Euro usw. und so fort. Die Frage war nun, welchen Einsatz man bereit wäre pro Wurf für so ein Spiel zu bezahlen? Zumal der erwartete Gewinn ja unendlich groß ist, müsste eigentlich jeder Einsatz passen. Kein Mensch würde aber mehr als ein paar Euro dafür ausgeben wollen, da die Chance auf einen unendlichen großen Gewinn ja unendlich klein ist. D’Alembert wollte damit aufzeigen, dass nicht alles mathematisch Fassbare auch eine Umsetzung findet und darauf hinweisen, dass Bernoullis Modell zwar schön sein mag, aber nicht zwingend praktikabel sein muss.