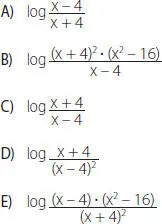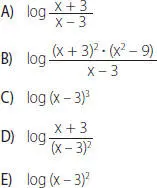C)3
D)0,4
E)0,5
7. ¿Cuál es el valor de la expresión log2128 + log 100 – log5625?
A)–10
B)–5
C)5
D)10
E)397
8. Si log 2 ≈ 0,30 y log 3 ≈ 0,47, ¿cuál es el valor de la expresión log 48 + log 6 – log 108?
A)0,17
B)0,43
C)0,9
D)1,07
E)1,37
9. ¿Cuál es el valor de la expresión log25• log58?
A)log 40
B)log 240
C)log 4
D)3
E)log 8
10. ¿Cuál de las siguientes expresiones es equivalente a logb?
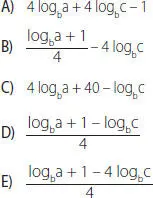
11. Si A = log155, ¿cómo se escribe log1581 en términos de A?
A)2A
B)4A
C)1 – A
D)A + 5
E)4 • (1 – A)
12. ¿Cuál de las siguientes afirmaciones es verdadera?
A)log 5  existe y su valor es
existe y su valor es 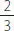 .
.
B)La expresión log ab se lee como logaritmo de aen base b.
C)log 749 existe y su valor es 2.
D)El argumento y la base de un logaritmo son números reales, además la base puede ser 1.
E)log 16 existe y su valor es 6.
13. Si P = log72, Q = log73 y R = log75, ¿cuál de las siguientes expresiones es igual a log735 – log730?
A)8R – P + Q
B)7 + R – P – Q
C)7 – P – Q
D)1 – P – Q
E)1 – P – Q – R
14. ¿Cuál es el valor de la expresión log2112?
A)7 • log 16
B)16 • log 27
C)4 + log 27
D)6
E)4 • log 27
15. ¿Cuál de las siguientes afirmaciones es verdadera?
A)El logaritmo de un producto es igual al producto de los logaritmos.
B)El valor del logaritmo cuya base es igual al argumento es siempre igual a 0.
C)El logaritmo de una suma es igual a la suma de los logaritmos.
D)La solución de una ecuación logarítmica se debe remplazar en la ecuación original para comprobar que sus logaritmos estén bien definidos.
E)La base de un logaritmo puede ser 1.
16. ¿Cuál es el valor de la expresión log464 + log 1.000 – log7343?
A)–3
B)–1
C)0
D)3
E)6
17. Si log 2 ≈ 0,30 y log 3 ≈ 0,47, ¿cuál es el valor de la expresión log 72 + log 36 – log 12?
A)0,17
B)0,77
C)1,41
D)1,54
E)2,31
18. ¿Cuál es resultado de log7?
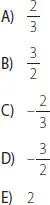
19. ¿Cuál es el valor de la expresión log42• log4256?
A)log 4128
B)log 4258
C)log 4512
D)2
E)8
20. Si log 2 ≈ 0,30 y log 3 ≈ 0,47, ¿cuál es el valor de la expresión log 64 + log 27 – log 36?
A)0,77
B)1,41
C)1,67
D)1,80
E)3,55
21. ¿Cuál(es) de las siguientes igualdades es (son) siempre verdadera(s)?
I.log b(p + q) = log bp • log bq
II.log aa – log bb = 0
III. 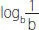 = –1
= –1
A)Solo I
B)Solo II
C)Solo III
D)Solo II y III
E)Solo I y II
22. ¿Cuál de las siguientes expresiones equivale a log (x – 4) + log (x2 – 16) – 2• log (x + 4)?
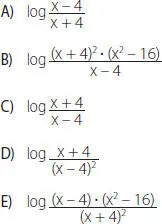
23. Para determinar el diámetro d (km) de un asteroide los astrónomos utilizan la fórmula: log d = 3,7 – 0,2• g, donde g es su magnitud absoluta.¿Cuál es la magnitud absoluta de un asteroide si su diámetro mide 10 km?
A)–2,65
B)1,04
C)7,5
D)23,5
E)13,5
24. ¿Cuál de las siguientes expresiones equivale a 2• log (x – 3) + log (x2 – 9) – log (x + 3)?
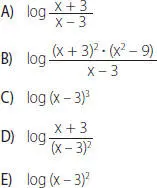
25. ¿Cuál de las siguientes igualdades representa una propiedad de los logaritmos?
A)log b(p • q) = log bp • log bq
B)log b(p + q) = log bp + log bq
C)log b(p + q) = log bp • log bq
D)log b(p • q) = log bp + log bq
E)log b(p – q) = log bp – log bq
26. ¿Cuál es la solución de la ecuación log (x + 4) = log (2x – 1)?
A)–5
B)–1
C)0
D)1
E)5
27. ¿Cuál es el valor de x en la expresión logx64 = 3?
A)1
B)2
C)3
D)4
E)5
28. ¿Cuál(es) de las expresiones siguientes es (son) igual(es) a log 2 + log 22?
I.3 log 2
II.log 2 3
III.log 2 • log 2 2
A)Solo I
B)Solo II
C)Solo I y II
D)Solo II y III
E)I, II y III
29. Si a y b – {1}, entonces logba = c si:
(1)b c= a
(2)c > 0
A) (1)por sí sola.
B) (2)por sí sola.
C)Ambas juntas, (1)y (2).
D)Cada una por sí sola, (1)o (2).
E)Se requiere información adicional.
Читать дальше

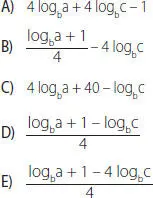
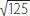 existe y su valor es
existe y su valor es 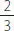 .
.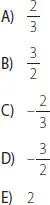
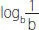 = –1
= –1