( )
4. Números irracionales
Todos los números racionales están representados por puntos sobre la recta numérica, pero ¿todos los puntos de la recta son representaciones de números racionales? La respuesta es NO. Existen otros números que junto a los números racionales completan a la recta numérica: los números irracionales.
DEFINICIÓN:Los números irracionales son los que no se pueden expresar como fracción. En símbolos:
I = {x / x no se puede expresar como fracción
Convertidos a la notación decimal son números con infinitas cifras no periódicas.
SIMBÓLICAMENTE:
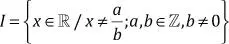
Ejemplos:
Los siguientes son números irracionales famosos. Están redondeados en la quinta cifra decimal, con lo cual se obtiene un valor aproximado bastante aceptable.
a. El número PI: = π ≈ 3,14159
b. El número e ≈ 2,71828
c. El número de oro: 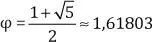
d. Raíces no exactas como son: 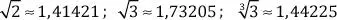

PI (π):es la relación que existe entre el perímetro y el diámetro de una circunferencia. Quiere decir que si divides el perímetro por el diámetro de cualquier circunferencia resulta el número π.
El número π tiene un valor de: 3,14159265…
Este número es de los más utilizados en matemáticas, física e ingeniería porque la circunferencia es un elemento muy común.
Ubicación exacta de 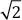
Con ayuda del Teorema de Pitágoras podemos ubicar de manera exacta el número 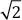 . Si construimos un triángulo rectángulo de catetos unitarios, la hipotenusa mide
. Si construimos un triángulo rectángulo de catetos unitarios, la hipotenusa mide 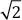 . Luego, con ayuda de un compás trasladamos la medida de la hipotenusa a la recta real.
. Luego, con ayuda de un compás trasladamos la medida de la hipotenusa a la recta real.
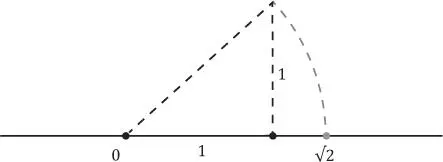

Teorema de Pitágoras
En todo triángulo rectángulo se cumple que el cuadrado de la medida de la hipotenusa es igual a la suma de los cuadrados de las medidas de los catetos.
Una operación en I es una manera de asociar a cada par de números irracionales, otro número irracional bien determinado. Las operaciones que se definen en este conjunto son la suma, la resta, la multiplicación, el cociente y la extracción de raíces (exceptuando la radicación de números negativos de índice par).
Las operaciones de suma, diferencia, producto, cociente y potenciación de números irracionales no siempre arrojan como resultado a otro irracional. Algunas veces los resultados son racionales.
5. Números reales
DEFINICIÓN:el conjunto de los números reales surge de la unión de los números racionales y de los irracionales. Se denota como 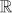 Comprende a todos los sistemas numéricos anteriores.
Comprende a todos los sistemas numéricos anteriores.
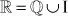

Se habla del orden en los números reales a través de la propiedad de tricotomía afirmando que dados n y m dos números reales, entonces se tiene exactamente una de las tres posibilidades:
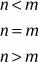
Al igual que en los conjuntos 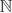 ,
, 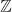 ,
, 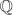 e I, los números reales se pueden representar en una recta, solo que en este caso no hay puntos discretos, sino se trata de una recta continua:
e I, los números reales se pueden representar en una recta, solo que en este caso no hay puntos discretos, sino se trata de una recta continua:
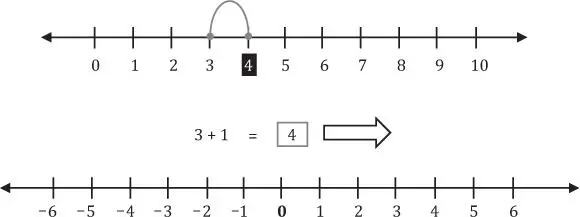
La recta 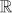 sobre la cual se representa a los números racionales e irracionales se llama recta real. A cada punto de esta recta se le asocia un único número real llamado coordenada o abscisa del punto y, recíprocamente, a cada punto de esa recta se le vincula un único número para que sea su coordenada. Si esta doble asignación se hace de manera que puntos distintos tengan coordenadas distintas y cada número sea coordenada de algún punto, se ha obtenido una correspondencia biunívoca entre la recta y el conjunto de los números reales. Esta asignación se denomina Sistema de Coordenadas Unidimensional.
sobre la cual se representa a los números racionales e irracionales se llama recta real. A cada punto de esta recta se le asocia un único número real llamado coordenada o abscisa del punto y, recíprocamente, a cada punto de esa recta se le vincula un único número para que sea su coordenada. Si esta doble asignación se hace de manera que puntos distintos tengan coordenadas distintas y cada número sea coordenada de algún punto, se ha obtenido una correspondencia biunívoca entre la recta y el conjunto de los números reales. Esta asignación se denomina Sistema de Coordenadas Unidimensional.
En general, dado un punto P cualquiera en la recta, al número real a se le llama coordenada o abscisa de P y se denota por P ( a ), que se lee: punto P de coordenada a .
Ejemplo:
Ubiquemos de forma aproximada los siguientes números en la recta real: 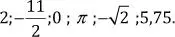
Solución
En forma de coordenadas, los números toman la forma:
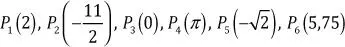 Que en la recta real están localizados así:
Que en la recta real están localizados así:

Una operación en 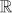 es una manera de asociar a cada par de números reales, otro número real bien determinado. Las operaciones que se definen en este conjunto son la suma, la multiplicación (la resta se considera como la suma de números de diferente signo y la división como la multiplicación de un número por el recíproco de otro, siempre cuando el segundo no sea cero), la radicación de números positivos y la radicación de índice impar de números negativos. Es decir, las operaciones que se definen en este conjunto son todas excepto dos:
es una manera de asociar a cada par de números reales, otro número real bien determinado. Las operaciones que se definen en este conjunto son la suma, la multiplicación (la resta se considera como la suma de números de diferente signo y la división como la multiplicación de un número por el recíproco de otro, siempre cuando el segundo no sea cero), la radicación de números positivos y la radicación de índice impar de números negativos. Es decir, las operaciones que se definen en este conjunto son todas excepto dos:
Читать дальше

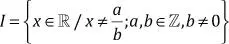
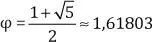
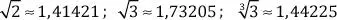

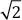


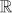 Comprende a todos los sistemas numéricos anteriores.
Comprende a todos los sistemas numéricos anteriores.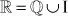

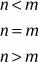
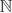 ,
, 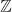 ,
, 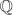 e I, los números reales se pueden representar en una recta, solo que en este caso no hay puntos discretos, sino se trata de una recta continua:
e I, los números reales se pueden representar en una recta, solo que en este caso no hay puntos discretos, sino se trata de una recta continua:
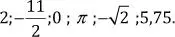
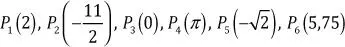 Que en la recta real están localizados así:
Que en la recta real están localizados así:











