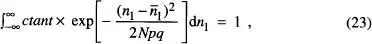
on hem estès la integral des de -∞ fins a +∞ perquè la contribució de 1'integrand és negligible quan 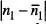 suficientment gran com perquè WN estiga lluny del valor corresponent al seu màxim. La integral de l' eq. (23)es pot reduir a la forma general (vegeu la taula 4)
suficientment gran com perquè WN estiga lluny del valor corresponent al seu màxim. La integral de l' eq. (23)es pot reduir a la forma general (vegeu la taula 4)
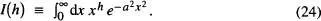

Taula 4
Quan la integral s'estén des de -∞ fins a +∞ el seu valor és igual al doble del valor tabulai si h es parell, i zero si h és imparell. En general, I ( h ) = [( h – l)/(2 a 2)] I ( h – 2) [de la Rubia i Brey, cap. 1; Reif, A.2–4], En el nostre cas, s'obté de l' eq. (23)i la taula 4que la ctant = 1/(2π Npq ) 1/2i, per tant,
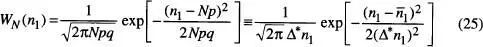
d'acord amb les eqs. (14) i (17). L' eq. (25)constitueix la denominada distribució de Gauss o gaussiana i coincideix amb la distribució binòmia quan N → ∞ per a aquells valors en què totes dues són apreciablement distintes de zero. Tanmateix, observem que la distribució de l' eq. (25)està definida (encara que és pràcticament nul·la) per a |n 1| < N i és a més simètrica respecte a 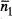 , la qual cosa no és el cas de la distribució binòmia si p ≠ q. No obstant l'anterior, el raonament que ha portat a l' eq. (25)és de naturalesa relativament general, per la qual cosa les distribucions gaussianes apareixen sovint en estadística quan es tracta amb nombres grans, i presenten l'avantatge respecte a les binòmies de ser molt més senzilles des del punt de vista pràctic.
, la qual cosa no és el cas de la distribució binòmia si p ≠ q. No obstant l'anterior, el raonament que ha portat a l' eq. (25)és de naturalesa relativament general, per la qual cosa les distribucions gaussianes apareixen sovint en estadística quan es tracta amb nombres grans, i presenten l'avantatge respecte a les binòmies de ser molt més senzilles des del punt de vista pràctic.
Podem tornar ara al cas de la partícula de moviment 1D tractat en la secció anterior i preguntar-nos per la probabilitat de trobar la partícula en una posició x entre x i x + dx, sent dx «microscòpicament gran» (d x » /) però suficientement petit com perquè es puga aplicar el càlcul diferencial. 8El pas de la variable discreta m = n l– n 2= 2 n 1– N a la variable contínua x es pot fer per mitjà de la relació (vegeu la fig. 10) w ( x )d x = WN ( m ) d x /2 l , ja que δ x = 2 1 en canviar m dues unitats quan n 1varia en una unitat. De l' eq. (25)reescrita per a m resulta immediatament
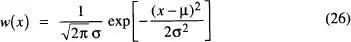
on x = ml , 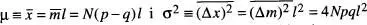 per al valor mitjà i la dispersió, d'acord amb la notació habitual en estadística matemàtica. Es pot provar que la distribució gaussiana de l' eq. (26)(també anomenada distribució normal) té les següents propietats: (i) està normalitzada a la unitat, (ii) compleix que
per al valor mitjà i la dispersió, d'acord amb la notació habitual en estadística matemàtica. Es pot provar que la distribució gaussiana de l' eq. (26)(també anomenada distribució normal) té les següents propietats: (i) està normalitzada a la unitat, (ii) compleix que 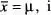 (iii) verifica que
(iii) verifica que 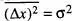 . Per comprovar-ho, només cal efectuar el canvi de variable y ≡ x - μ i avaluar les integrals resultants amb ajuda de la taula 4[de la Rubia i Brey, cap. 1].
. Per comprovar-ho, només cal efectuar el canvi de variable y ≡ x - μ i avaluar les integrals resultants amb ajuda de la taula 4[de la Rubia i Brey, cap. 1].
La forma típica d'una distribució de Gauss és la representada en la fig. 11. Es pot demostrar 8directament de l' eq. (26)que l'àrea compresa entre les ordenades μ - σ i μ + σ i l'eix d'abscisses és 0.683 [Reif, A.5]. Aquesta àrea arriba a ser de 0.997 per al cas de l'interval [μ - 3σ, μ + 3σ], molt propera ja a l'àrea total corresponent a l'interval entre -∞ i +∞ que és 1 per la condició de normalització. La distribució esdevé per tant més aguda com menor és a. En el límit σ → 0, w ( x ) tendeix a la funció delta de Dirac [Reif, A. 7; de la Rubia i Brey, cap. 1],
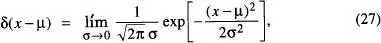
tal com es mostra en la fig. 12.
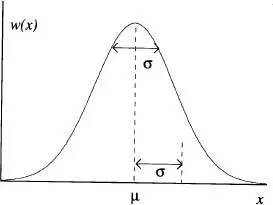
Figura 11
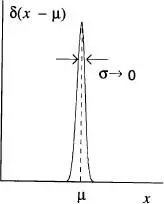
Figura 12
Al llarg d'aquesta secció hem restringit el tractament a una funció de distribució amb una sola variable aleatòria. La descripció estadística d'una situació en la qual intervinga més d'una variable requereix només generalitzacions directes de les funcions de distribució de probabilitats corresponents [Reif, cap. 1], tal com veurem durant el curs.
3.4 Distribució de Poisson
Quan la probabilitat p és petita però N és molt gran de manera que Np ≡ λ és finit, es pot obtindré una nova distribució (denominada distribució de Poisson) com a cas límit de la binòmia. La distribució de Poisson es fa servir per a valors petits de n 1. En efecte, si fem n 1≡ n « N i considerem el quocient
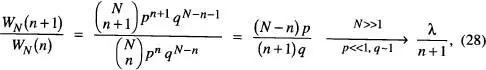
d'on WN ( n ) = WN ( O ) λ n/ n !. Per la condició de normalització, WN (0) = e -λ, i obtenim així
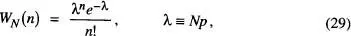
que és la funció de distribució de Poisson. És immediat demostrar que 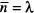 i
i 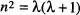 utilitzant mètodes similars als emprats en les eqs. (14) i (16), respectivament, d'on
utilitzant mètodes similars als emprats en les eqs. (14) i (16), respectivament, d'on 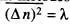 . La distribució de Poisson apareix en molts problemes de Física Estadística: un gas distribuït en un determinat volum [Kittel i Kroemer, cap. 6], processos d'adsorció sobre superfícies [Kittel i Kroemer, A.C], desintegracions radioactives i emissions termoiòniques [Lands- berg, cap. 26], etc. Si considerem una desintegració radioactiva, p. ex., i prenem com a succés elemental l'emissió o no d'una partícula en un instant temporal entre t i t + dt , assignant p = γd t « 1 a l'emissió i q = γd t ~ 1 a la no-emissió, aleshores sobre un total d'intents N = t /d t » 1 distribuïts al llarg d'un temps macroscopic t , la probabilitat d'emissió de n partícules ve donada per la distribució binòmia
. La distribució de Poisson apareix en molts problemes de Física Estadística: un gas distribuït en un determinat volum [Kittel i Kroemer, cap. 6], processos d'adsorció sobre superfícies [Kittel i Kroemer, A.C], desintegracions radioactives i emissions termoiòniques [Lands- berg, cap. 26], etc. Si considerem una desintegració radioactiva, p. ex., i prenem com a succés elemental l'emissió o no d'una partícula en un instant temporal entre t i t + dt , assignant p = γd t « 1 a l'emissió i q = γd t ~ 1 a la no-emissió, aleshores sobre un total d'intents N = t /d t » 1 distribuïts al llarg d'un temps macroscopic t , la probabilitat d'emissió de n partícules ve donada per la distribució binòmia
Читать дальше

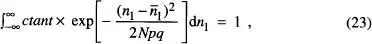
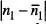 suficientment gran com perquè WN estiga lluny del valor corresponent al seu màxim. La integral de l' eq. (23)es pot reduir a la forma general (vegeu la taula 4)
suficientment gran com perquè WN estiga lluny del valor corresponent al seu màxim. La integral de l' eq. (23)es pot reduir a la forma general (vegeu la taula 4)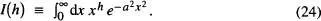

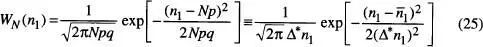
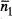 , la qual cosa no és el cas de la distribució binòmia si p ≠ q. No obstant l'anterior, el raonament que ha portat a l' eq. (25)és de naturalesa relativament general, per la qual cosa les distribucions gaussianes apareixen sovint en estadística quan es tracta amb nombres grans, i presenten l'avantatge respecte a les binòmies de ser molt més senzilles des del punt de vista pràctic.
, la qual cosa no és el cas de la distribució binòmia si p ≠ q. No obstant l'anterior, el raonament que ha portat a l' eq. (25)és de naturalesa relativament general, per la qual cosa les distribucions gaussianes apareixen sovint en estadística quan es tracta amb nombres grans, i presenten l'avantatge respecte a les binòmies de ser molt més senzilles des del punt de vista pràctic.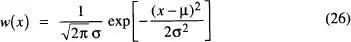
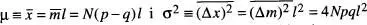 per al valor mitjà i la dispersió, d'acord amb la notació habitual en estadística matemàtica. Es pot provar que la distribució gaussiana de l' eq. (26)(també anomenada distribució normal) té les següents propietats: (i) està normalitzada a la unitat, (ii) compleix que
per al valor mitjà i la dispersió, d'acord amb la notació habitual en estadística matemàtica. Es pot provar que la distribució gaussiana de l' eq. (26)(també anomenada distribució normal) té les següents propietats: (i) està normalitzada a la unitat, (ii) compleix que 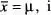 (iii) verifica que
(iii) verifica que 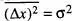 . Per comprovar-ho, només cal efectuar el canvi de variable y ≡ x - μ i avaluar les integrals resultants amb ajuda de la taula 4[de la Rubia i Brey, cap. 1].
. Per comprovar-ho, només cal efectuar el canvi de variable y ≡ x - μ i avaluar les integrals resultants amb ajuda de la taula 4[de la Rubia i Brey, cap. 1].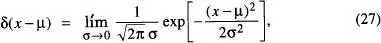


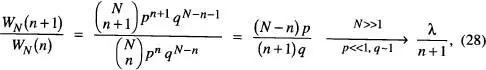
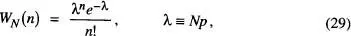
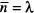 i
i 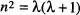 utilitzant mètodes similars als emprats en les eqs. (14) i (16), respectivament, d'on
utilitzant mètodes similars als emprats en les eqs. (14) i (16), respectivament, d'on 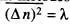 . La distribució de Poisson apareix en molts problemes de Física Estadística: un gas distribuït en un determinat volum [Kittel i Kroemer, cap. 6], processos d'adsorció sobre superfícies [Kittel i Kroemer, A.C], desintegracions radioactives i emissions termoiòniques [Lands- berg, cap. 26], etc. Si considerem una desintegració radioactiva, p. ex., i prenem com a succés elemental l'emissió o no d'una partícula en un instant temporal entre t i t + dt , assignant p = γd t « 1 a l'emissió i q = γd t ~ 1 a la no-emissió, aleshores sobre un total d'intents N = t /d t » 1 distribuïts al llarg d'un temps macroscopic t , la probabilitat d'emissió de n partícules ve donada per la distribució binòmia
. La distribució de Poisson apareix en molts problemes de Física Estadística: un gas distribuït en un determinat volum [Kittel i Kroemer, cap. 6], processos d'adsorció sobre superfícies [Kittel i Kroemer, A.C], desintegracions radioactives i emissions termoiòniques [Lands- berg, cap. 26], etc. Si considerem una desintegració radioactiva, p. ex., i prenem com a succés elemental l'emissió o no d'una partícula en un instant temporal entre t i t + dt , assignant p = γd t « 1 a l'emissió i q = γd t ~ 1 a la no-emissió, aleshores sobre un total d'intents N = t /d t » 1 distribuïts al llarg d'un temps macroscopic t , la probabilitat d'emissió de n partícules ve donada per la distribució binòmia










