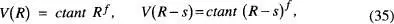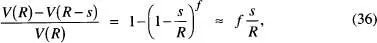Com hem vist en la secció 1, l'enumeració dels estats microscòpics possibles d'un sistema és un pas previ a tota descripció estadística. Per tal de procedir a aquesta enumeració, cal subdividir els camps de variació de q i p en intervals discrets 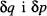 , amb
, amb 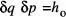 (vegeu la fig. 14), on h0 és una constant de dimensions de moment angular [Reif, cap. 2]. L'espai fàsic queda dividit aleshores en cel·les iguals de volum
(vegeu la fig. 14), on h0 és una constant de dimensions de moment angular [Reif, cap. 2]. L'espai fàsic queda dividit aleshores en cel·les iguals de volum 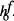 L'espai fàsic accessible és la regió limitada per «hipersuperfícies» definides per funcions del tipus F ({ q }) = V o f ({ q,p }) = E , sent-hi Vi Eel volum i l'energia del sistema, o qualsevol altra que represente una condició de contorn sobre el sistema. L'estat microscopic del sistema s'especifica establint els f valors de q i de p dins dels intervals
L'espai fàsic accessible és la regió limitada per «hipersuperfícies» definides per funcions del tipus F ({ q }) = V o f ({ q,p }) = E , sent-hi Vi Eel volum i l'energia del sistema, o qualsevol altra que represente una condició de contorn sobre el sistema. L'estat microscopic del sistema s'especifica establint els f valors de q i de p dins dels intervals 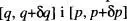 respectius, és a dir, associant una cel·la de volum
respectius, és a dir, associant una cel·la de volum 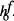 de l'espai fàsic de 2 f dimensions. A efectes pràctics es pot considerar com un punt representatiu de l'estat microscopic del sistema en l'espai fàsic (vegeu la fig. 14). Una variació en l'espai fàsic accessible al sistema deguda a un canvi en les seues condicions de contorn comporta sempre una variació en el nombre d'estats microscòpics del sistema.
de l'espai fàsic de 2 f dimensions. A efectes pràctics es pot considerar com un punt representatiu de l'estat microscopic del sistema en l'espai fàsic (vegeu la fig. 14). Una variació en l'espai fàsic accessible al sistema deguda a un canvi en les seues condicions de contorn comporta sempre una variació en el nombre d'estats microscòpics del sistema.
La fig. 15 mostra la trajectòria fàsica en l'espai ( x,p ) d'una partícula que segueix un moviment 1D amb energia E = p 2/2 m dins d'una capsa de longitud 2a [de la Rubia i Brey. cap. 2]. Els segments de punts indiquen el canvi quasi instantani en el sentit del moment lineal p de la partícula en col·lidir elàsticament amb les parets de la capsa en x = ±a , considerades aquestes com a barreres «infinites» de potencial. Per simplicitat, s'ha omès la subdivisió en cel·les de la fig. 14 en la trajectòria de la fig. 15.
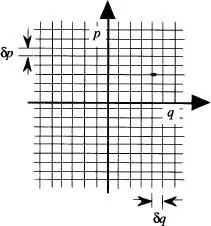
Figura 14
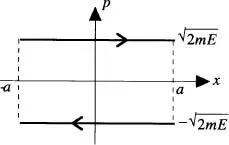
Figura 15
La fig. 16a representa l'espai fàsic per a un oscil·lador harmònic que segueix un moviment ID amb una energia entre E i E + δ E , sent 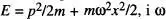 , la freqüència angular de l'oscil·lador. Un interval donat áx correspon a un nombre major de cel·les entre les dues el lipses si x ≈ A que si x ≈ 0. És més probable que l'oscil·lador es trobe al voltant de A (on la seua velocitat es molt petita) que al voltant de 0 (on la seua velocitat es màxima) [Reif, cap. 2].
, la freqüència angular de l'oscil·lador. Un interval donat áx correspon a un nombre major de cel·les entre les dues el lipses si x ≈ A que si x ≈ 0. És més probable que l'oscil·lador es trobe al voltant de A (on la seua velocitat es molt petita) que al voltant de 0 (on la seua velocitat es màxima) [Reif, cap. 2].
La regió accessible de l'espai fàsic està formada per l'àrea compresa entre les dues el lipses de la fig. 16a, i conté un cert nombre de cel les (estats de la partícula) de volum arbitrari h 0corresponents a parells de valors ( x, p ). En una descripció clàssica no existeix una grandària mínima de cel·la, de manera que cada estat del sistema es pot representar per un volum arbitràriament petit i, en el límit, per un punt. En una descripció quàntica, però, l'espai fàsic està quan- titzat en cel·les de grandària mínima 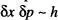 , sent-hi h la constant de Planck. Així, p. ex., si quantitzem l'energia d'un oscil·lador de manera que
, sent-hi h la constant de Planck. Així, p. ex., si quantitzem l'energia d'un oscil·lador de manera que 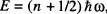 , l'àrea total (una el lipse) An tancada pel nivell d'energia n ve donada pel producte
, l'àrea total (una el lipse) An tancada pel nivell d'energia n ve donada pel producte 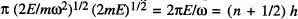 , de manera que l'espai fàsic queda dividit en cel·les d'àrea A n+l- An = h (vegeu la fig. 16b).
, de manera que l'espai fàsic queda dividit en cel·les d'àrea A n+l- An = h (vegeu la fig. 16b).
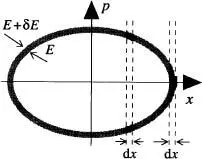
Figura 16a
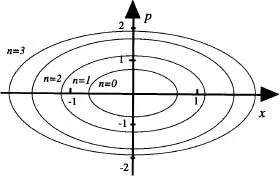
Figura 16b
La quantització de l'espai fàsic en cel·les de grandària definida h 3Nper a un sistema de N partícules en moviment 3D suposa obviar l'arbitrarietat de la descripció clàssica respecte a la grandària de cel·la, i permet obtindré la constant de Planck mitjançant la relació existent entre Ventropia absoluta i el nombre d'estats quàntics accessibles per a un sistema, tal com veurem en capítols posteriors. Històricament, aquesta determinació va contribuir a atorgar credibilitat a la Mecànica Quàntica, i fou realitzada uns pocs anys abans que Sommerfeld presentara les seues famoses regles de quantització [Gopal, cap. 2; Kittel i Kroemer, cap. 5].
5.2 Sistemes de molts graus de llibertat
L'enumeració dels estats accessibles per a un sistema amb molts graus de llibertat (diguem f ~ NA , on NA és el nombre d'Avogadro) mena a resultats a primera vista sorprenents. Considerarem a tall d'exemple el comportament del quocient format pel volum d'una escorça esfèrica de gruix s « R en un espai de/dimensions i el volum d'una hiperesfera de radi R en l'esmentat espai quan l'energia total del sistema canvia lleugerament [McQuarrie, problema 7–10]. El radi R ve donat per l'energia total E del sistema i el gruix s de l'escorça per la variació d'energia δ E (vegeu la fig. 17).
Considerem dues hiperesferes en l'espai de f dimensions, una de radi R i una altra de radi R - s (vegeu la fig. 17). Els seus volums vénen donats per les expressions
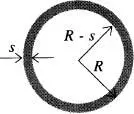
Figura 17
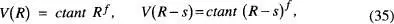
de manera que el quocient entre el volum de l'escorça situada entre ambdues hiperesferes i el volum de la hiperesfera anterior és
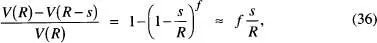
ja que s « R. Aquest quocient és negligible en un espai amb f = 3, però no ho és quan f ~ NA , com és típic d'un sistema macroscopic. Per elaborar més aquest argument, suposem que les N ~ NA partícules del sistema només posseeixen moviments de translació que contribueixen a l'energia total en la forma
Читать дальше

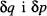 , amb
, amb 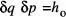 (vegeu la fig. 14), on h0 és una constant de dimensions de moment angular [Reif, cap. 2]. L'espai fàsic queda dividit aleshores en cel·les iguals de volum
(vegeu la fig. 14), on h0 és una constant de dimensions de moment angular [Reif, cap. 2]. L'espai fàsic queda dividit aleshores en cel·les iguals de volum 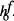 L'espai fàsic accessible és la regió limitada per «hipersuperfícies» definides per funcions del tipus F ({ q }) = V o f ({ q,p }) = E , sent-hi Vi Eel volum i l'energia del sistema, o qualsevol altra que represente una condició de contorn sobre el sistema. L'estat microscopic del sistema s'especifica establint els f valors de q i de p dins dels intervals
L'espai fàsic accessible és la regió limitada per «hipersuperfícies» definides per funcions del tipus F ({ q }) = V o f ({ q,p }) = E , sent-hi Vi Eel volum i l'energia del sistema, o qualsevol altra que represente una condició de contorn sobre el sistema. L'estat microscopic del sistema s'especifica establint els f valors de q i de p dins dels intervals 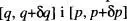 respectius, és a dir, associant una cel·la de volum
respectius, és a dir, associant una cel·la de volum 

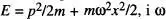 , la freqüència angular de l'oscil·lador. Un interval donat áx correspon a un nombre major de cel·les entre les dues el lipses si x ≈ A que si x ≈ 0. És més probable que l'oscil·lador es trobe al voltant de A (on la seua velocitat es molt petita) que al voltant de 0 (on la seua velocitat es màxima) [Reif, cap. 2].
, la freqüència angular de l'oscil·lador. Un interval donat áx correspon a un nombre major de cel·les entre les dues el lipses si x ≈ A que si x ≈ 0. És més probable que l'oscil·lador es trobe al voltant de A (on la seua velocitat es molt petita) que al voltant de 0 (on la seua velocitat es màxima) [Reif, cap. 2].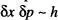 , sent-hi h la constant de Planck. Així, p. ex., si quantitzem l'energia d'un oscil·lador de manera que
, sent-hi h la constant de Planck. Així, p. ex., si quantitzem l'energia d'un oscil·lador de manera que 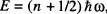 , l'àrea total (una el lipse) An tancada pel nivell d'energia n ve donada pel producte
, l'àrea total (una el lipse) An tancada pel nivell d'energia n ve donada pel producte 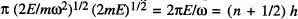 , de manera que l'espai fàsic queda dividit en cel·les d'àrea A n+l- An = h (vegeu la fig. 16b).
, de manera que l'espai fàsic queda dividit en cel·les d'àrea A n+l- An = h (vegeu la fig. 16b).