La dispersió es pot ara avaluar de la forma
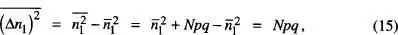
on hem fet ús de
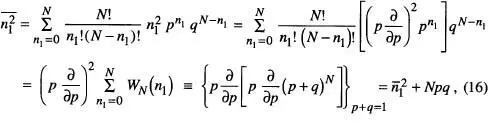
amb 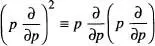 . Així queda que
. Així queda que
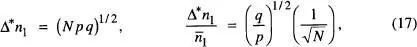
amb 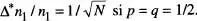 . O siga, la desviació quadràtica mitjana (i, amb això, el recorregut dins del qual n 1està distribuïda) augmenta amb
. O siga, la desviació quadràtica mitjana (i, amb això, el recorregut dins del qual n 1està distribuïda) augmenta amb 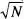 , però l'amplitud relativa d'aquest recorregut disminueix amb
, però l'amplitud relativa d'aquest recorregut disminueix amb 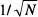 . Aquests resultats, que es poden comprovar a partir de la fig. 9a–b per a una distribució binòmia amb p = q = 1/2, són de gran importància en Física Estadística. Finalment, com que
. Aquests resultats, que es poden comprovar a partir de la fig. 9a–b per a una distribució binòmia amb p = q = 1/2, són de gran importància en Física Estadística. Finalment, com que 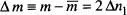 , veiem de seguida que
, veiem de seguida que 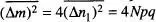 , fent servir l' eq. (15).
, fent servir l' eq. (15).
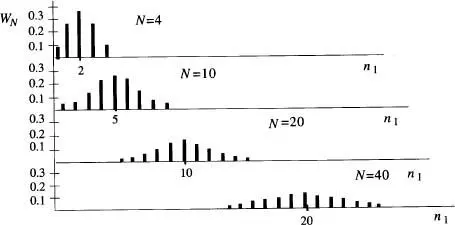
Figura 9a
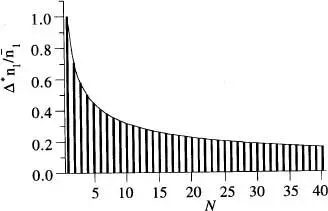
Figura 9b
3.3 Distribució de Gauss
La distribució de probabilitats de Gauss o distribució gaussiana es pot obtindré com a límit de la distribució binòmia quan N pren valors grans. Abans de demostrar aquest resultat, exposarem de forma breu com es pot passar d'una distribució de probabilitats W de variable aleatòria ui discreta a una altra distribució w de variable u contínua [de la Rubia i Brey, cap. 1].
Una variable aleatòria contínua es defineix mitjançant la funció densitat (o distribució) de probabilitat w(u) el significat de la qual és tal que
w(u)du = probabilitat que la variable u prenga un valor dins de l'interval comprès entre u i u+du.
Suposem una variable aleatòria discreta ui amb distribució de probabilitat W ( ui ). Per a major senzillesa, admetrem que la diferència entre dos valors consecutius de la variable anterior pren un valor constant δ u , de manera que u i+1- ui = δ u , ∀ i . Admetrem a més que δ u és suficientment petita com perquè puguem definir un du que, tot i permetent la utilització del càlcul diferencial, siga molt més gran que δ u (vegeu la fig. 10).

Figura 10
Finalment, suposarem que la variació de W amb ui és suficientment lenta com perquè W ( ui ) siga aproximadament constant per a tots els ui situats dins un mateix interval d'amplitud d u. Tenint en compte que en l'interval d u hi ha d u /δ u valors permesos de la variable discreta, w ( u )d u = W (punts en l'interval d u ) x d u /δ u , que permet passar d'una distribució discreta a una altra contínua i viceversa. Totes les definicions referents a valors mitjans i normalitzacions vistes per a una variable discreta es poden traslladar al cas continu substituint sumatoris per integrals, i tenint en compte que es possible estendre el rang de qualsevol variable aleatòria contínua des de -∞ a +∞ simplement considerant nuls els valors de la funció densitat de probabilitat corresponents a valors no possibles de la variable aleatòria. L' eq. (9)queda aleshores així
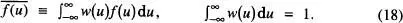
Estem ja en condicions d'estudiar el límit de la distribució binòmia en l' eq. (6)quan N → ∞. Aquest límit està tractat de forma rigorosa en la bibliografia [de la Rubia i Brey, cap. 1; Reif, cap. 1], i ací ens limitarem tan sols a esbossar-ne els detalls més importants. Si N pren un valor gran, la distribució binòmia tendeix a presentar un màxim molt pronunciat al voltant de 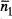 , qüestió que es pot verificar fàcilment només recalculant els resultats de la fig. 8 per a N » 20. Aquest resultat suggereix la possibilitat d'efectuar un desenvolupament 6de In WN ( n 1) al voltant de
, qüestió que es pot verificar fàcilment només recalculant els resultats de la fig. 8 per a N » 20. Aquest resultat suggereix la possibilitat d'efectuar un desenvolupament 6de In WN ( n 1) al voltant de 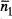 en l' eq. (6). Per efectuar aquest desenvolupament, considerarem n j com un nombre real, admetent que quan N és molt gran podem substituir un gran nombre de punts WN ( n 1) corresponents als valors enters de n 1per una funció contínua que passe per tots els punts. Escrivim aleshores
en l' eq. (6). Per efectuar aquest desenvolupament, considerarem n j com un nombre real, admetent que quan N és molt gran podem substituir un gran nombre de punts WN ( n 1) corresponents als valors enters de n 1per una funció contínua que passe per tots els punts. Escrivim aleshores
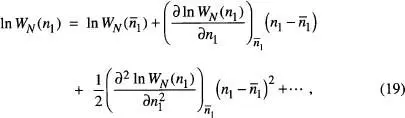
amb
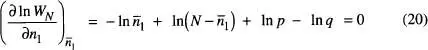
i
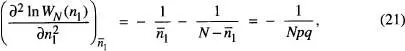
on hem fet ús de l'aproximació de Stirling de l' eq. (4)per avaluar els logaritmes. No analitzarem la convergència del desenvolupament efectuat en l' eq. (19)detalladament 7[de la Rubia i Brey, cap. 1]. Admetrem que podem negligir els termes d'ordre superior al segon i escriure
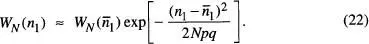
Ara bé, si  substituint
substituint  en WN , la distribució de probabilitats de l' eq. (22)no estaria normalitzada a causa de les aproximacions realitzades. Per procedir a normalitzar-la, considerarem que tant WN com n 1es poden tractar com a funcions pràcticament contínues quan N pren valors grans, de manera que la condició de normalització és
en WN , la distribució de probabilitats de l' eq. (22)no estaria normalitzada a causa de les aproximacions realitzades. Per procedir a normalitzar-la, considerarem que tant WN com n 1es poden tractar com a funcions pràcticament contínues quan N pren valors grans, de manera que la condició de normalització és
Читать дальше

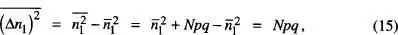
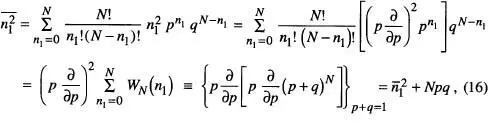
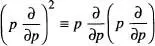 . Així queda que
. Així queda que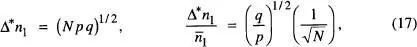
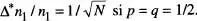 . O siga, la desviació quadràtica mitjana (i, amb això, el recorregut dins del qual n 1està distribuïda) augmenta amb
. O siga, la desviació quadràtica mitjana (i, amb això, el recorregut dins del qual n 1està distribuïda) augmenta amb 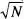 , però l'amplitud relativa d'aquest recorregut disminueix amb
, però l'amplitud relativa d'aquest recorregut disminueix amb 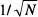 . Aquests resultats, que es poden comprovar a partir de la fig. 9a–b per a una distribució binòmia amb p = q = 1/2, són de gran importància en Física Estadística. Finalment, com que
. Aquests resultats, que es poden comprovar a partir de la fig. 9a–b per a una distribució binòmia amb p = q = 1/2, són de gran importància en Física Estadística. Finalment, com que 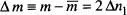 , veiem de seguida que
, veiem de seguida que 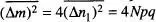 , fent servir l' eq. (15).
, fent servir l' eq. (15).


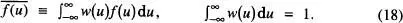
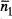 , qüestió que es pot verificar fàcilment només recalculant els resultats de la fig. 8 per a N » 20. Aquest resultat suggereix la possibilitat d'efectuar un desenvolupament 6de In WN ( n 1) al voltant de
, qüestió que es pot verificar fàcilment només recalculant els resultats de la fig. 8 per a N » 20. Aquest resultat suggereix la possibilitat d'efectuar un desenvolupament 6de In WN ( n 1) al voltant de 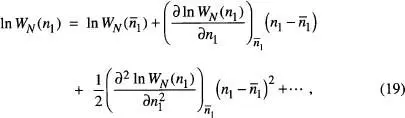
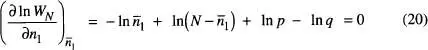
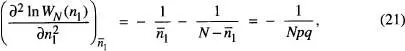
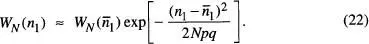
 substituint
substituint  en WN , la distribució de probabilitats de l' eq. (22)no estaria normalitzada a causa de les aproximacions realitzades. Per procedir a normalitzar-la, considerarem que tant WN com n 1es poden tractar com a funcions pràcticament contínues quan N pren valors grans, de manera que la condició de normalització és
en WN , la distribució de probabilitats de l' eq. (22)no estaria normalitzada a causa de les aproximacions realitzades. Per procedir a normalitzar-la, considerarem que tant WN com n 1es poden tractar com a funcions pràcticament contínues quan N pren valors grans, de manera que la condició de normalització és










