Si es considera l'eix x al llarg del carrer amb l'origen x = 0 en la ubicació del fanal, la posició del borratxo després de N passos de longitud individual / és x = ml , amb m un nombre enter (positiu, negatiu o zero). La pregunta típica és en aquest cas: ¿quina és la probabilitat que el borratxo estiga just en determinada posició x? Per contestar-la, s'ha de considerar un gran nombre Nde borratxos similars deambulant en carrers semblants, tot i que seria també possible repetir l'experiment Nvegades amb la mateixa persona, si aquesta roman- guera en condicions d'intoxicació anàlogues. En el primer cas, la pregunta és, ¿quina serà la fracció de borratxos situats en x = ml , després de N passos? I per al segon seria: ¿quantes vegades (fracció del total) acabarà el contumaç individu en la posició x = ml després de Nsèries de N passos cadascuna?
La Física no es preocupa habitualment per l'esdevenir d'un borratxo, però el problema del camí aleatori apareix en situacions de gran interès com ara la difusió d'una molècula en un gas o la conformació d'una cadena polimèrica en una dissolució. A més a més, els sistemes amb dos estats de probabilitats p i q són molt habituals en magnetisme i física-química de superfícies, p. ex. A l'últim, el problema del camí aleatori permet una exposició elemental de molts conceptes estadístics, i per tant anem a tractar-ho detalladament a continuació per al cas més asèptic d'una partícula que segueix un moviment 1D.
Pretenem calcular la probabilitat WN (m) de trobar la partícula en la posició x = ml , després d'una seqüència de N desplaçaments elementals (passos) dels quals n 1són cap a la dreta i n 2cap a l'esquerra, de manera que m = n 1- n 2i N = n 1+ n 2. Aquesta probabilitat és, tenint en compte la hipòtesi d'independència estadística per als passos,

amb n2 = N - n 1. Notem que el primer factor dóna compte del fet que qualsevol seqüència de n 1passos a la dreta i n 2a l'esquerra mena a x = ( n 1- n 2) l , independentment de l'ordre en què aquests es realitzen. 5La funció de probabilitat de l' eq. (6)s'anomena distribució binòmia , i rep el seu nom de la condició de normalització
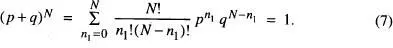
En funció del desplaçament net m , l' eq. (6)es pot escriure com
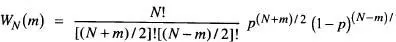
sent-hi ( N + m ) = 2 n 1i ( N - m ) = 2 n 2dos enters parells. Per aplicació de l' eq. (6)(o l'eq. 8) al cas N = 20 passos i p = q = 1/2 és immediat obtindré la probabilitat WN ( n 1) de la fig. 8. La simetria de la distribució entorn del valor mitjà 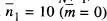 es perd si p ≠ q , és a dir,
es perd si p ≠ q , és a dir, 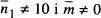 en el cas asimètric.
en el cas asimètric.
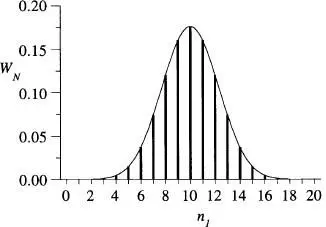
Figura 8
En general, coneguda una distribució de probabilitat P(ui) d'una variable aleatòria ui que pot prendre qualsevol dels M valors discrets u l, u 2, …, uM , el valor mitjà de qualsevol funció f(u) és
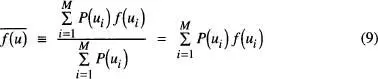
on hem fet servir la condició de normalització per a P ( ui ).
Alguns dels valors mitjans més útils en Física Estadística són el valor mitjà de la variable u ,

i els valors mitjans  , denominats moments d'ordre n. Són també d'interès el valor mitjà de la desviació
, denominats moments d'ordre n. Són també d'interès el valor mitjà de la desviació 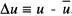 , anomenat moment central de primer ordre ,
, anomenat moment central de primer ordre ,
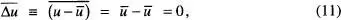
i la dispersió ( o moment central de segon ordre)
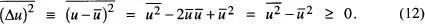
Notem que en aquest cas cada terme de la suma en l' eq. (9)és positiu o nul, ja que 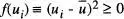 i també P ( ui ) ≥ 0. Com menys agrupats estiguen els valors de «¿ a l'entorn de u , més gran serà la dispersió. Es poden definir altres valors mitjans, com el moment d'ordre enèsim (À«) namb n > 2, però són de menor utilitat. A partir de l' eq. (12)es defineix la desviació quadràtica mitjana o desviació estàndard com
i també P ( ui ) ≥ 0. Com menys agrupats estiguen els valors de «¿ a l'entorn de u , més gran serà la dispersió. Es poden definir altres valors mitjans, com el moment d'ordre enèsim (À«) namb n > 2, però són de menor utilitat. A partir de l' eq. (12)es defineix la desviació quadràtica mitjana o desviació estàndard com

La magnitud ∆ * u és una mesura lineal de l'amplitud del recorregut en què la variable u està distribuïda. El quocient 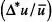 informa sobre la desviació relativa de la variable u respecte del valor mitjà, i és de gran importància en Física Estadística. El coneixement més complet que es pot tindré d'una variable aleatòria és la seua distribució de probabilitat, la qual cosa permet calcular tots els seus moments. A la inversa, és possible obtindré aquesta distribució si es coneixen tots els moments. El coneixement dels primers moments és, però, suficient per a la major part dels problemes en Física Estadística.
informa sobre la desviació relativa de la variable u respecte del valor mitjà, i és de gran importància en Física Estadística. El coneixement més complet que es pot tindré d'una variable aleatòria és la seua distribució de probabilitat, la qual cosa permet calcular tots els seus moments. A la inversa, és possible obtindré aquesta distribució si es coneixen tots els moments. El coneixement dels primers moments és, però, suficient per a la major part dels problemes en Física Estadística.
Estem en condicions d'aplicar ara les definicions i resultats de les eqs. (9) –(13) al cas particular de la distribució binòmia de l' eq. (6). A partir de l' eq. (10), resulta
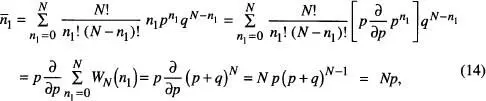
prenent p i q com a dues variables independents a l'efecte de la derivació, i substituint ( p + q ) = 1 una vegada efectuada aquesta. Conegut 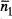 ,
, 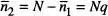 , d'on
, d'on 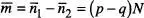 . Aquests resultats es podrien haver anticipat: com que p és la probabilitat d'un pas a la dreta, el nombre mitjà de passos a la dreta d'un total de N és Np. Notem que si p = q , aleshores
. Aquests resultats es podrien haver anticipat: com que p és la probabilitat d'un pas a la dreta, el nombre mitjà de passos a la dreta d'un total de N és Np. Notem que si p = q , aleshores 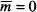 tal com es pot esperar en una situació simètrica.
tal com es pot esperar en una situació simètrica.
Читать дальше


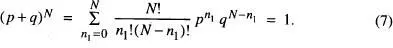
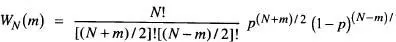
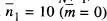 es perd si p ≠ q , és a dir,
es perd si p ≠ q , és a dir, 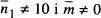 en el cas asimètric.
en el cas asimètric.
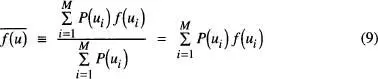

 , denominats moments d'ordre n. Són també d'interès el valor mitjà de la desviació
, denominats moments d'ordre n. Són també d'interès el valor mitjà de la desviació 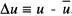 , anomenat moment central de primer ordre ,
, anomenat moment central de primer ordre ,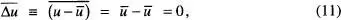
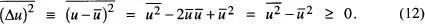
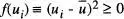 i també P ( ui ) ≥ 0. Com menys agrupats estiguen els valors de «¿ a l'entorn de u , més gran serà la dispersió. Es poden definir altres valors mitjans, com el moment d'ordre enèsim (À«) namb n > 2, però són de menor utilitat. A partir de l' eq. (12)es defineix la desviació quadràtica mitjana o desviació estàndard com
i també P ( ui ) ≥ 0. Com menys agrupats estiguen els valors de «¿ a l'entorn de u , més gran serà la dispersió. Es poden definir altres valors mitjans, com el moment d'ordre enèsim (À«) namb n > 2, però són de menor utilitat. A partir de l' eq. (12)es defineix la desviació quadràtica mitjana o desviació estàndard com
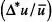 informa sobre la desviació relativa de la variable u respecte del valor mitjà, i és de gran importància en Física Estadística. El coneixement més complet que es pot tindré d'una variable aleatòria és la seua distribució de probabilitat, la qual cosa permet calcular tots els seus moments. A la inversa, és possible obtindré aquesta distribució si es coneixen tots els moments. El coneixement dels primers moments és, però, suficient per a la major part dels problemes en Física Estadística.
informa sobre la desviació relativa de la variable u respecte del valor mitjà, i és de gran importància en Física Estadística. El coneixement més complet que es pot tindré d'una variable aleatòria és la seua distribució de probabilitat, la qual cosa permet calcular tots els seus moments. A la inversa, és possible obtindré aquesta distribució si es coneixen tots els moments. El coneixement dels primers moments és, però, suficient per a la major part dels problemes en Física Estadística.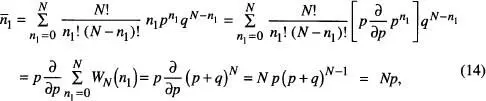
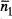 ,
, 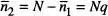 , d'on
, d'on 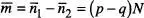 . Aquests resultats es podrien haver anticipat: com que p és la probabilitat d'un pas a la dreta, el nombre mitjà de passos a la dreta d'un total de N és Np. Notem que si p = q , aleshores
. Aquests resultats es podrien haver anticipat: com que p és la probabilitat d'un pas a la dreta, el nombre mitjà de passos a la dreta d'un total de N és Np. Notem que si p = q , aleshores 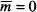 tal com es pot esperar en una situació simètrica.
tal com es pot esperar en una situació simètrica.










