A 10. Dibuixa en l'espai fàsic adequat la trajectòria d'un punt que represente una pilota que cau lliurement a terra des d'una altura h , si el xoc és: a) elàstic, i b) inelàstic.
Sol.- à) Es tracta de paràboles en pz, b ) Coincideix amb a) , tret que ara les paràboles acaben degenerant en un punt per la dissipació d'energia.
A 11. Descriu les corbes de l'espai fàsic (z, pz) corresponents al moviment en una dimensió d'una partícula en el si d'un camp gravitatori uniforme. Representa en l'esmentat espai fàsic les trajectòries de dues partícules abans i després de sofrir una col·lisió elàstica en un punt z = zc.
Sol.- Es tracta de paràboles en pz. La col·lisió elàstica suposa «saltar» a una altra paràbola pròxima.
B 7. Un oscil·lador lineal amortit està descrit per l'equació
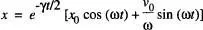
sent-hi ω » γ. Determina i dibuixa la seua trajectòria fàsica. Troba la variació temporal de l'espai fàsic.
A 12. Determina el nombre total de microestats i macroestats possibles per a un sistema fictici compost per 4 partícules distingibles a, b, c i d de nivells d'energia 0, ε, 2ε i 3ε quan l'energia total del sistema és 2ε. ¿Com es modifica el nombre de microestats si el nivell 0 està 2 vegades degenerat i el nivell e tres vegades degenerat?
Sol.- 2 macroestats i 10 microestats. El nombre total de microestats és ara 248.
1. És possible, això no obstant, seguir l'evolució temporal d'un conjunt reduït de N partícules (p. ex., N = 10 2-10 3), i obtindré en cada instant informació macroscòpica d'aquest a partir de la resolució de les equacions de moviment microscòpiques. Aquest és el punt de vista de la Dinàmica Molecular, un dels desenvolupaments moderns de la Física Estadística [Heermann, cap. 3; Cuadros et al., Revista Española de Física 7 (1993) 19]
2 Analitzarem detalladament els conceptes de partícula indistingible i distingible al llarg dels temes següents.
3 Una disposició particular amb N = 3 i n = 4 seria • • | | • | , que indica que la primera caixa conté 2 objectes, la tercera 1 objecte i la segona i la quarta, cap objecte. Les parets primera (1) i darrera (5) no s'han representat.
4 El problema 1D es pot generalitzar a 2D, 3D, etc. En 2D, és habitual considerar camins aleatoris en direccions perpendiculars, la qual cosa dóna lloc al denominat «borratxo ortogonal» [Lim, problema 2155] de gran aplicació en Física de Polímers [Gupta, cap. 8].
5 Aquest factor es pot entendre fàcilment si pensem que, encara que el nombre de formes diferents d'efectuar N passos és N !, aquest nombre es redueix a 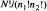 si n¡ són indistin- giblement d'un primer tipus i n2 d'un segon tipus.
si n¡ són indistin- giblement d'un primer tipus i n2 d'un segon tipus.
6 La raó del fet que es desenvolupe lnW N(i no WN) és que el logaritme és una funció de variació amb n¡ molt més lenta que WN , de manera que el desenvolupament en sèrie de potències de ln WN convergeix molt més ràpid que el de WN [Reif, cap. 1].
7 El terme d'ordre k > 2 en el desenvolupament de l' eq. (19)és proporcional a 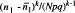 [de la Rubia i Brey, cap. 1], de manera que l' eq. (22)constitueix una bona aproximació en tant que N siga gran i p, q no siguen excessivament petits. (Si p o q són molt petits, aleshores la distribució binòmia tendeix a la de Poisson, com veurem després.)
[de la Rubia i Brey, cap. 1], de manera que l' eq. (22)constitueix una bona aproximació en tant que N siga gran i p, q no siguen excessivament petits. (Si p o q són molt petits, aleshores la distribució binòmia tendeix a la de Poisson, com veurem després.)
8 En un problema de difusió d'un àtom en un sòlid, p. ex., I ~ 10 -10m = 1Â (espaciat de la xarxa) però les mesures a escala macroscòpica involucren escales L ~ 10 -6m = 1 um o majors.
9 En general, podem fer servir el canvi de variable t = (x - µ)/σ per obtindré la funció error
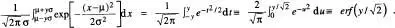
12 És immediat demostrar de les eqs. (35) i (37) que 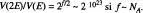
13 Considerem la fig. 13, p. ex. Si assignem un moment magnètic individual +µ. a l'espín en l'estat ↑, aleshores a l'estat macroscopic de magnetització M = +mµ li corresponen 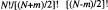 estats microscòpics possibles. Si m = 0 i N = NA , aleshores el nombre anterior és
estats microscòpics possibles. Si m = 0 i N = NA , aleshores el nombre anterior és 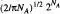 aplicant l'aproximació de Stirling (vegeu l'eq. 5), de manera que a un estat macroscopic particular li corresponen ~ 10 10 x 1022estats microscòpics diferents.
aplicant l'aproximació de Stirling (vegeu l'eq. 5), de manera que a un estat macroscopic particular li corresponen ~ 10 10 x 1022estats microscòpics diferents.
14 S'atribueix a Planck, i així mateix a Keynes, l'afirmació: «una innovació científica important rares vegades s'obri camí guanyant adeptes a poc a poc i fent conversos entre els seus oponents… el que sol ocórrer és que aquests moren a poc a poc, mentre que la generació següent es familiaritza ja amb les noves idees des de la seua infantesa» [Fernández Pineda i García Velarde, cap. 2].
15 En realitat, fou Planck qui obtingué aquesta equació en la forma en que apareix en la tomba de Boltzmann (sense cap constant additiva) a partir de la correspondència trobada originalment pel propi Boltzmann entre els canvis en S i W [Pathria, cap. 1]
16 S'ha comparat la importància d'aquest mètode, que és la base de moltes de les aplicacions actuals de la Física Estadística, amb la de les equacions de Maxwell de l'Electromagnetisme [Pathria, Introd.]. Einstein assajà també una formulació de la Física Estadística alternativa a la de Gibbs en una sèrie de tres articles publicats en Annalen der Physik (1902—1904). Com en el cas de Gibbs (noteu el llarg títol de la seua obra), la preocupació principal d'Einstein era fonamentar les lleis de la Termodinàmica sobre la base de les equacions de la mecànica i el càlcul de probabilitats [Montero i Solé, Revista de Física , 1 (1993) 22].
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

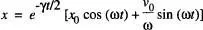
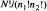 si n¡ són indistin- giblement d'un primer tipus i n2 d'un segon tipus.
si n¡ són indistin- giblement d'un primer tipus i n2 d'un segon tipus.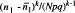 [de la Rubia i Brey, cap. 1], de manera que l' eq. (22)constitueix una bona aproximació en tant que N siga gran i p, q no siguen excessivament petits. (Si p o q són molt petits, aleshores la distribució binòmia tendeix a la de Poisson, com veurem després.)
[de la Rubia i Brey, cap. 1], de manera que l' eq. (22)constitueix una bona aproximació en tant que N siga gran i p, q no siguen excessivament petits. (Si p o q són molt petits, aleshores la distribució binòmia tendeix a la de Poisson, com veurem després.)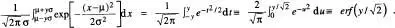
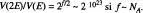
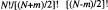 estats microscòpics possibles. Si m = 0 i N = NA , aleshores el nombre anterior és
estats microscòpics possibles. Si m = 0 i N = NA , aleshores el nombre anterior és 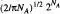 aplicant l'aproximació de Stirling (vegeu l'eq. 5), de manera que a un estat macroscopic particular li corresponen ~ 10 10 x 1022estats microscòpics diferents.
aplicant l'aproximació de Stirling (vegeu l'eq. 5), de manera que a un estat macroscopic particular li corresponen ~ 10 10 x 1022estats microscòpics diferents.










