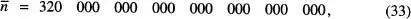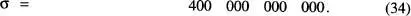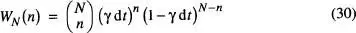
que d'acord amb les eqs. (28)–(29) es pot aproximar per la de Poisson

per a N » 1 amb λ ≡ N γd t = γ t finit. Altres problemes es poden tractar de manera semblant a l'anterior.
4. Sistemes de N espins
Moltes de les distribucions de probabilitat que apareixen en Física Estadística són gaussianes de màxims molt pronunciats. Per il·lustrar aquest fet, considerarem un sistema de N espins independents separats espacialment, cadascun dels quals pot trobar-se en un estat ↑ o en un estat ↓ [Rosser, cap. 2; Kittel i Kroemer, cap. 1]. Per simplicitat, suposarem que les probabilitats associades a aquests estats són iguals, p = q = 1/2, si bé el cas asimètric és també força interessant [Reif (2), cap. 1]. La fig. 13 mostra esquemàticament el sistema considerat.
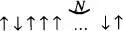
Figura 13
Evidentment, el nombre total d'estats microscòpics possibles per al sistema de N espins és gT = 2 N , i la probabilitat de trobar n ≤ N dels espins en l'estat ↑ és, d'acord amb l' eq. (6),
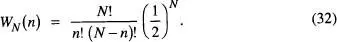
De les eqs. (14) i (17), 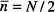 ,
, 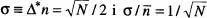 . Si N = 3, aleshores
. Si N = 3, aleshores 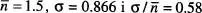 . En aquest cas les desviacions de n respecte del valor mitjà
. En aquest cas les desviacions de n respecte del valor mitjà 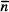 (que anomenarem «fluctuacions» entorn de l'esmentat valor mitjà) són importants. Notem que una mesura del valor absolut de les dites fluctuacions és
(que anomenarem «fluctuacions» entorn de l'esmentat valor mitjà) són importants. Notem que una mesura del valor absolut de les dites fluctuacions és 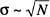 , i del valor relatiu d'aquestes,
, i del valor relatiu d'aquestes, 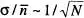 . La situació canvia dràsticament per a un sistema macroscopic de N = 6.4 x 10 23espins (aproximadament un mol d'espins): ara
. La situació canvia dràsticament per a un sistema macroscopic de N = 6.4 x 10 23espins (aproximadament un mol d'espins): ara 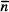 = 3.2 x 10 23, σ = 4 x 10 11,
= 3.2 x 10 23, σ = 4 x 10 11, 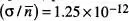 , i la distribució de probabilitats esdevé extremadament abrupta entorn de
, i la distribució de probabilitats esdevé extremadament abrupta entorn de 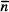 . En efecte, si prenem arbitràriament l'amplària de la distribució com a 2σ (vegeu la fig. 11), aleshores
. En efecte, si prenem arbitràriament l'amplària de la distribució com a 2σ (vegeu la fig. 11), aleshores 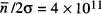 , la qual cosa significa que la distància al llarg de 1'abscissa des de n = 0 fins a
, la qual cosa significa que la distància al llarg de 1'abscissa des de n = 0 fins a 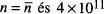 l'amplària de la distribució 2σ. ÉS a dir,
l'amplària de la distribució 2σ. ÉS a dir,
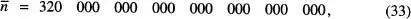
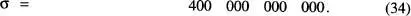
Per a N gran, la distribució binòmia ≈ distribució gaussiana. Hem vist que per a una distribució gaussiana, aproximadament el 68% dels valors de n cauen dins d'un interval d'amplària ±σ centrat en  , xifra que s'eleva fins al 99.7% per a un interval d'amplària ±3σ. ES pot demostrar que per a una distribució gaussiana, la probabilitat d'obtindré un valor de n que es desvie del valor mitjà
, xifra que s'eleva fins al 99.7% per a un interval d'amplària ±3σ. ES pot demostrar que per a una distribució gaussiana, la probabilitat d'obtindré un valor de n que es desvie del valor mitjà  en més de ±100σ és de l'ordre de 10 -2174[Rosser, cap. 2]. Com a mitjana, s'hauria de mostrejar doncs un total de 10 2174estats microscòpics com el mostrat en la fig. 13 per trobar-ne un el valor de n del qual es desviarà de
en més de ±100σ és de l'ordre de 10 -2174[Rosser, cap. 2]. Com a mitjana, s'hauria de mostrejar doncs un total de 10 2174estats microscòpics com el mostrat en la fig. 13 per trobar-ne un el valor de n del qual es desviarà de 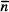 en més de 100σ. Podem elaborar encara més aquest argument si supo-sem, p. ex., que cada espín canvia d'estat cada 10 -12s, o siga, 10 12vegades per segon. 10L'estat microscopic del sistema de la fig. 13 canvia amb la condició que només un dels N espins canvie de sentit, i la resta roman en les seues posicions originals. Per tant, per a un sistema de 6.4 x 10 23espins hi ha 6.4 x 10 23x 10 12= 6.4 x 10 35canvis en l'estat microscopic per segon. L'edat de la Terra és d'uns 4.5 x 10 9anys = 1.42 x 10 17s, la qual cosa permet un total de 10 53estats microscòpics distints en el sistema d'espins. Com a mitjana, per obtindré una desviació de
en més de 100σ. Podem elaborar encara més aquest argument si supo-sem, p. ex., que cada espín canvia d'estat cada 10 -12s, o siga, 10 12vegades per segon. 10L'estat microscopic del sistema de la fig. 13 canvia amb la condició que només un dels N espins canvie de sentit, i la resta roman en les seues posicions originals. Per tant, per a un sistema de 6.4 x 10 23espins hi ha 6.4 x 10 23x 10 12= 6.4 x 10 35canvis en l'estat microscopic per segon. L'edat de la Terra és d'uns 4.5 x 10 9anys = 1.42 x 10 17s, la qual cosa permet un total de 10 53estats microscòpics distints en el sistema d'espins. Com a mitjana, per obtindré una desviació de 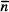 més gran que ±100σ, s'hauria d'esperar un temps de l'ordre de 10 2174/10 53= 10 2121edats de la Terra. Aquest és el significat de la paraula mai en Física Estadística. 11
més gran que ±100σ, s'hauria d'esperar un temps de l'ordre de 10 2174/10 53= 10 2121edats de la Terra. Aquest és el significat de la paraula mai en Física Estadística. 11
5. Espai fàsic. Sistemes de molts graus de llibertat
5.1 Espai fàsic
En Física Estadística clàssica, el nombre f de coordenades de posició independents necessàries per a definir un sistema s'anomena nombre de graus de llibertat del sistema. Així un conjunt de N partícules puntuals que segueix un moviment 3D té f = 3 N , ja que són necessàries tres coordenades de posició per partícula. Per descriure un sistema de N partícules amb coordenades generalitzades qi i moments generalitzats Pies fa servir un espai de 2 f = 3 N + 3 N = 6 N dimensions en el cas d'un moviment 3D. Aquest espai s'anomena espai de fases del sistema o espai Г, a diferència de l'espai μ constituït per les 3 + 3 = 6 dimensions característiques del moviment 3D d'una de les N partícules del sistema. Un punt de l'espai de fases determina l'estat del sistema a través de les posicions i moments de les N partícules.
Читать дальше

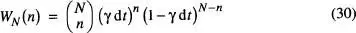

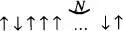
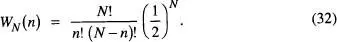
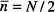 ,
, 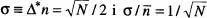 . Si N = 3, aleshores
. Si N = 3, aleshores 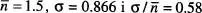 . En aquest cas les desviacions de n respecte del valor mitjà
. En aquest cas les desviacions de n respecte del valor mitjà 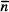 (que anomenarem «fluctuacions» entorn de l'esmentat valor mitjà) són importants. Notem que una mesura del valor absolut de les dites fluctuacions és
(que anomenarem «fluctuacions» entorn de l'esmentat valor mitjà) són importants. Notem que una mesura del valor absolut de les dites fluctuacions és 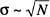 , i del valor relatiu d'aquestes,
, i del valor relatiu d'aquestes, 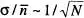 . La situació canvia dràsticament per a un sistema macroscopic de N = 6.4 x 10 23espins (aproximadament un mol d'espins): ara
. La situació canvia dràsticament per a un sistema macroscopic de N = 6.4 x 10 23espins (aproximadament un mol d'espins): ara 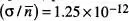 , i la distribució de probabilitats esdevé extremadament abrupta entorn de
, i la distribució de probabilitats esdevé extremadament abrupta entorn de 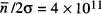 , la qual cosa significa que la distància al llarg de 1'abscissa des de n = 0 fins a
, la qual cosa significa que la distància al llarg de 1'abscissa des de n = 0 fins a 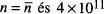 l'amplària de la distribució 2σ. ÉS a dir,
l'amplària de la distribució 2σ. ÉS a dir,