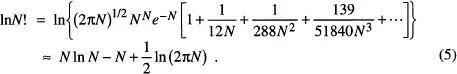Tal com hem avançat al final de la secció anterior, un pas previ al tractament estadístic consisteix en l'enumeració dels estats microscòpics d'un sistema de N partícules, la qual cosa involucra sovint nombres combinatoris. Efectuada aquesta enumeració, el càlcul de la probabilitat d'un estat i dels valors mitjans de les magnituds físiques necessita els conceptes de probabilitat i distribució de probabilitat. Dedicarem aquesta secció a una breu revisió de la combinatòria matemàtica, i la següent secció a aspectes relacionats amb la probabilitat.
La taula 1mostra algunes de les equacions del càlcul combinatori que farem servir al llarg d'aquest curs particularitzades al cas de N objectes («partícules») a distribuir en n capses («nivells» si s'efectua la identificació anterior). Les equacions de la taula 1corresponen al nombre de disposicions g(N,n ) distintes de les N partícules en els n nivells (suposem que no existeix degeneració en els nivells) per al cas de partícules distingibles i indistingibles, 2i es poden justificar sobre la base d'arguments senzills. Per exemple, per a N objectes distingibles a distribuir entre n capses sense cap restricció en el nombre d'objectes per capsa, g(N,n) = nN. Si els objectes foren indistingibles, el problema d'avaluar g(N,n ) es redueix ara a comptar el nombre de disposicions possibles per a una sèrie composta per N objectes iguals + (n - 1) parets, ja que n capses contigües suposen (n+1) parets, de les quals la nombre 1 i la (n + 1) ocupen posicions fixes. 3Evidentment, aquest nombre és 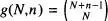 Si impo sem la condició d'un sol objecte per capsa, amb n > N , aleshores el nombre de disposicions seria
Si impo sem la condició d'un sol objecte per capsa, amb n > N , aleshores el nombre de disposicions seria 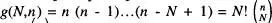 per a objectes distingibles i
per a objectes distingibles i 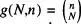 per a objectes indistingibles, ja que el nombre de permutacions que podem realitzar entre els objectes en les capses sense donar lloc a cap disposició nova és precisament N ! Finalment, l'equació per a les permutacions amb repetició de N objectes distingibles distribuïts de manera que n'hi ha Ni d'ells en la capsa i es pot obtindré a partir de l'equació
per a objectes indistingibles, ja que el nombre de permutacions que podem realitzar entre els objectes en les capses sense donar lloc a cap disposició nova és precisament N ! Finalment, l'equació per a les permutacions amb repetició de N objectes distingibles distribuïts de manera que n'hi ha Ni d'ells en la capsa i es pot obtindré a partir de l'equació

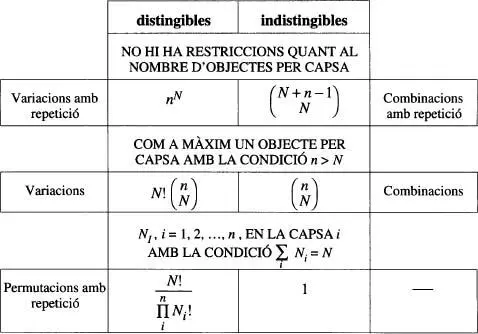
Taula 1
Si utilitzem la nomenclatura d'estats i partícules, l'existència de degeneracions gi en cada nivell i d'energia ε i dóna lloc al fet que a cada nivell li cor- responguen diversos estats, i es pot tractar com es mostra en la taula 2, on hem particularitzat la teoria combinatòria a les tres estadístiques que apareixen en aquest curs: l'estadística clàssica de Maxwell-Boltzmann (MB) i les estadístiques quàntiques de Bose-Einstein (BE) i Fermi-Dirac (FD).
Quan es consideren distribucions de N partícules en Física Estadística, generalment s'ha d'avaluar no N ! sinó ln N !. Quan N » 1 (en sistemes macroscòpics, N ~ NA ≈ 6 x 10 23), es pot efectuar la següent aproximació


Taula 2
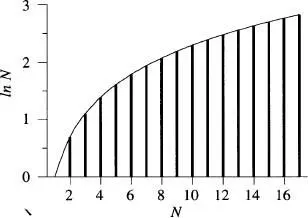
Figura 7
d'on N ! ≈ NN e-N. En l' eq. (4), hem tingut present que per a valors grans de N , la suma que apareix en aquesta es pot aproximar per la integral (≡ àrea tancada sota la corba In N vs. N de la fig. 7).
El resultat mostrat en l' eq. (4)es denomina aproximació de Stirling , i és molt emprada en Física Estadística. Un valor encara més exacte és [Kittel i Kroemer, A.l; Reif, A.6]
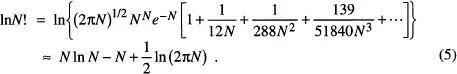
La taula 3mostra diversos valors de In N ! calculats directament i mitjançant les aproximacions de les eqs. (4) i (5). La desviació (en %) fa referència a la diferència entre aquestes darreres equacions.
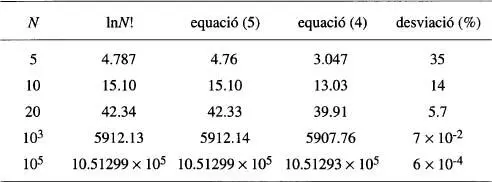
Taula 3
3. Probabilitat. Distribucions binòmia, de Gauss i de Poisson
3.1 Probabilitat
Definim la probabilitat experimental o probabilitat a posteriori d'un succés com el límit, si n'hi ha, del quocient entre el nombre d'assaigs favorables al succés i el nombre total d'assaigs realitzats, quan aquest darrer tendeix a infinit. Aquest límit es calcula mitjançant una extrapolació dels resultats obtinguts, i un succés per al qual existeix el límit (és a dir, per al qual es pot definir una probabilitat a posteriori) es diu que és un succés aleatori , i el procés corresponent s'anomena procés aleatori. A cadascun dels successos d'un procés aleatori se li pot assignar un nombre u de manera que W(u) siga la probabilitat del succés. La variable u es coneix amb el nom genèric de variable aleatòria o estocàstica.
Es suposen coneguts els conceptes elementals de la probabilitat [de la Rubia i Brey, cap.l; Stark i Woods, cap.l]. Per descriure una situació des del punt de vista estadístic, és a dir, en termes de probabilitats, cal considerar un conjunt o col·lectiu de Nsistemes ( N→ ∞) preparats de manera semblant. Per exemple, és possible donar una descripció estadística del llançament d'un dau considerant que un gran nombre de daus semblants es llancen en circumstàncies similars. Alternativament, es pot també llançar el mateix dau un nombre Nde vegades en circumstàncies semblants. La probabilitat d'un determinat succés es defineix com la fracció (nombre d'experiments en què es produeix aquest succés) / (nombre total d'experiments), de manera que la suma de probabilitats és igual a la unitat.
En aquells casos en què no hi ha cap raó perquè determinat succés aleatori es presente amb major freqüència que la resta, és possible assignar una probabilitat a priori igual per a tots i cadascun dels successos possibles. Aquest seria el cas dels successos aleatoris cara/creu per a una moneda o dels successos possibles per a un dau no carregat.
3.2 Distribució binòmia
Anem a analitzar detalladament molts dels conceptes probabilístics i estadístics que apareixeran durant el curs en un cas particular de gran importància en Física Estadística: el problema del camí aleatori [Reif, cap. 1 ; de la Rubia i Brey, cap. 1]. Aquest problema es pot formular de manera un tant col·loquial de la forma següent. Un borratxo parteix d'un fanal en un carrer seguint un moviment 41D. La condició d'intoxicació etílica es tradueix en el fet que cada pas a esquerra o dreta és independent del pas precedent. La probabilitat que el pas siga cap a la dreta és p , i que el pas ho siga cap a l'esquerra q , amb q = 1 - p. En general, p ≠ q (el carrer podria estar inclinat, p. ex.).
Читать дальше

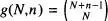 Si impo sem la condició d'un sol objecte per capsa, amb n > N , aleshores el nombre de disposicions seria
Si impo sem la condició d'un sol objecte per capsa, amb n > N , aleshores el nombre de disposicions seria 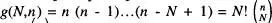 per a objectes distingibles i
per a objectes distingibles i 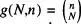 per a objectes indistingibles, ja que el nombre de permutacions que podem realitzar entre els objectes en les capses sense donar lloc a cap disposició nova és precisament N ! Finalment, l'equació per a les permutacions amb repetició de N objectes distingibles distribuïts de manera que n'hi ha Ni d'ells en la capsa i es pot obtindré a partir de l'equació
per a objectes indistingibles, ja que el nombre de permutacions que podem realitzar entre els objectes en les capses sense donar lloc a cap disposició nova és precisament N ! Finalment, l'equació per a les permutacions amb repetició de N objectes distingibles distribuïts de manera que n'hi ha Ni d'ells en la capsa i es pot obtindré a partir de l'equació