• El conocimiento adquirido debe tener un alto grado de aplicabilidad no sólo endógena, sino, básicamente, de carácter exógeno. Pero no basta: el estudiante debe reconocer este hecho y saberlo expresar a través oportunas situaciones: debe tener la sensación que el conocimiento adquirido influencia su competencia que resulta útil y evaluable.
• ¿Qué sucede en el proceso, cómo viene analizado antes y registrado después el nivel de calidad de la evolución cognitiva? De este punto se ocupa el “control”. El control interviene, incluso si parece paradójico, en vía preliminar, en el momento de proyectar el currículo o, por lo menos, la parte específica del proyecto de la evaluación; pero está siempre presente para alcanzar una re-proyectación constante, para articular formas de regulación y de autorregulación. Precisamente estas son las características que determinan un sistema abierto respecto a uno cerrado. Esto implica una actividad de tipo diverso de las pruebas de evaluación “usuales”, recurriendo a la formulación de conjeturas, su verifica y su defensa, al análisis del dominio de situaciones diversas que caen bajo el mismo conocimiento, a la redacción de textos, diseños, gráficos,.. Pero ¿cómo reconocer si las técnicas de control (entendido en este sentido) son adecuadas? Podemos decir que un control es adecuado sí ese mismo produce informaciones adecuadas para ser usadas a fin de mejorar las competencias de cada uno de los estudiantes y el proceso individual de construcción de conocimiento.
• La investigación actual sobre la evaluación, reflejando una dirección general que podemos pensar común a toda la didáctica de la matemática, está dando mucha importancia a la motivación y a los aspectos afectivos. Sobre estos aspectos debemos centrarnos, para ayudar al estudiante a crecer también en el gusto de tomar decisiones. Por ejemplo, si el estudiante hace preguntas sobre el procedimiento que debe seguir en una actividad, es contraproducente, desde este punto de vista, sugerir como proseguir; por el contrario, es aún más productivo motivar, responder con otra pregunta que lleve a reflexionar sobre la situación, sugerir un análisis, una analogía, una estrategia que el estudiante no había visto o pensado; es inútil dar indicaciones que aumenten el nivel de la propuesta, dirigiéndola a un nivel mayor (de un ejemplo a la generalización; de un ejercicio a la comparación estructural; de la defensa de una conjetura a la demostración; sólo para dar algún ejemplo concreto). Siempre en este ámbito, queremos subrayar la importancia que tiene el hecho que el estudiante entienda que el docente decidió aceptar su situación personal, ya sea en términos de elecciones, ya sea en lo que respecta una eventual condición de objetiva diversidad.
• Una moderna idea de evaluación, que tenga en cuenta de los resultados de la investigación, debe plantearse el problema de la formación. De una parte, la formación de los estudiantes sobre el tema: explicitar las problemática, hacerlas evidentes y contribuir a hacer sí que incluso la evaluación sea elemento vivo y presente en la vida de aula. Por otra parte, no siempre obvio en la formación inicial o en servicio de los docentes.
• Una moderna idea de evaluación, que se proponga como innovadora, no puede prescindir de la exigencia que esta sea coherente y ecuánime, de forma tal, que se gane la confianza de todos, de los estudiantes, de sus familias, de los docentes, de la noosfera. La coherencia más compleja de obtener parece ser aquella entre lo que se hace en matemática y cómo este hacer viene evaluado; este punto debería ser desarrollado dando valoraciones explícitas. En cuanto a la equidad, esto implica que cada estudiante deba sentirse parte no sólo del proceso de enseñanza - aprendizaje, sino también del proceso de evaluación. La coherencia implica un desarrollo eficaz, el reconocimiento de valores diversos, la profesionalidad del docente. Por último, es importante que todos tengan confianza en el proceso de evaluación, porque este pueda ser reconocido como el producto externo en el cual se configura la ética de las intenciones didácticas.
Es en todo esto que se reconoce un tentativo de fundar una moderna visión de la evaluación sobre la base de los actuales resultados; lejos de ser, como podría pensarse, sólo un conjunto de palabras vacías, lo descrito hasta aquí es, por el contrario, un instrumento preciso y concreto que aporta un fundamento nuevo, riguroso y ágil, a la profesionalidad del docente.
1.5. Intervenir y evaluar la especificidad de un fracaso
Como ya lo habíamos dicho, seguirán los cinco capítulos del 2 al 6, en cada uno de los cuales se presenta uno de los cinco componentes del aprendizaje de la matemática; en cada uno de ellos, se harán propuestas de actividades centradas en la evaluación específica.
¿Por qué? Porque el fracaso de un estudiante en matemática puede ser, en más: la mayor parte de las veces lo es, específico. Es un hecho conocido y confirmado por muchos docentes.
Un estudiante pudo haber construido en concepto auspiciado, pero no sabe usarlo para realizar un algoritmo, o para revolver un problema; no lo sabe comunicar o sólo aprendió a representarlo semióticamente.
Otro estudiante pudo no haber construido el concepto deseado, sin embargo sabe operar algorítmicamente sobre aspectos relacionados con este concepto; por ejemplo, el estudiante de la escuela media no ha entendido el sentido conceptual de la proporción 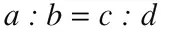 pero sabe que el producto de los medios es igual al producto de los extremos:
pero sabe que el producto de los medios es igual al producto de los extremos: 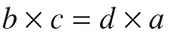 y lo usa para efectuar algoritmos; pero, no sabe usar las proporciones cuando se trata de resolver problemas, no sabe comunicar el sentido de lo que está haciendo, sabe representar la proporción sólo si la reconoce en la forma algebraica. Un caso que se tiene con mucha frecuencia en la escuela superior o en al universidad: estudiantes que saben calcular límites o derivadas, pero que no han elaborado el concepto ni del uno ni de la otra.
y lo usa para efectuar algoritmos; pero, no sabe usar las proporciones cuando se trata de resolver problemas, no sabe comunicar el sentido de lo que está haciendo, sabe representar la proporción sólo si la reconoce en la forma algebraica. Un caso que se tiene con mucha frecuencia en la escuela superior o en al universidad: estudiantes que saben calcular límites o derivadas, pero que no han elaborado el concepto ni del uno ni de la otra.
Ahora que el sentido de lo que aquí proponemos ha sido clarificado, podemos ir un poco más rápido, con ejemplos aún más específicos, formulados de forma mucho más cercana a la cotidianidad: estudiantes que saben transformar semióticamente ecuaciones, pero que no saben conceptualmente que están haciendo; estudiantes que... La lista podría continuar, con ejemplos fácilmente evidenciados a cualquier nivel escolástico.
Esta es la respuesta a la pregunta: el análisis detallado de cada una de las componentes no es y no pretende ser la declaración falsa e ingenua que estos aprendizajes actúan de forma separada; este análisis es sólo un proyecto discursivo por comodidad para ayudar en la evaluación específica, en la recuperación, actuando directamente sobre las causas y no sobre los errores.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

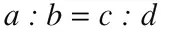 pero sabe que el producto de los medios es igual al producto de los extremos:
pero sabe que el producto de los medios es igual al producto de los extremos: 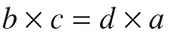 y lo usa para efectuar algoritmos; pero, no sabe usar las proporciones cuando se trata de resolver problemas, no sabe comunicar el sentido de lo que está haciendo, sabe representar la proporción sólo si la reconoce en la forma algebraica. Un caso que se tiene con mucha frecuencia en la escuela superior o en al universidad: estudiantes que saben calcular límites o derivadas, pero que no han elaborado el concepto ni del uno ni de la otra.
y lo usa para efectuar algoritmos; pero, no sabe usar las proporciones cuando se trata de resolver problemas, no sabe comunicar el sentido de lo que está haciendo, sabe representar la proporción sólo si la reconoce en la forma algebraica. Un caso que se tiene con mucha frecuencia en la escuela superior o en al universidad: estudiantes que saben calcular límites o derivadas, pero que no han elaborado el concepto ni del uno ni de la otra.










