Martha Isabel Fandiño Pinilla - Múltiples aspectos del aprendizaje de la matemática

Se evalúa para tomar decisiones sobre el ambiente clase. En una hipótesis constructivista, es dado por cierto que la implicación personal es el primer paso hacia la construcción de un conocimiento, hacia el aprendizaje; por tanto, evaluar si esta fue alcanzada es un paso de extraordinaria importancia. De esto deriva, como consecuencia, que el ambiente dominante en aula es fundamental. Esto significa que es de vital importancia que haya, por así decirlo, en una primera instancia, confianza en la acción del docente. Preguntas como: ¿Los alumnos se dan cuenta si al docente le gusta enseñar matemática?, ¿La resolución de los problemas y el descubrimiento son aspectos habituales en la hora de matemática?, ¿Los alumnos tienen la oportunidad de explorar y de experimentar sin sentir la presión de estar bajo juicio? ¿En el momento de dar una nota, se tiene en cuenta algo más que la respuesta correcta a un ejercicio?,... asumen importancia estratégica en la formación del ambiente de clase adecuado.

Se evalúa para comunicar a los alumnos lo que es importante. Los alumnos son capaces (es más, son habilísimos) de reconocer aquello que implícitamente el docente considera importante; por ejemplo, si frente a un trabajo escrito el docente revisa el proceso seguido por el estudiante, sólo cuando la respuesta final no es la correcta, con el fin de encontrar el error, implícitamente está enseñando que el proceso no es importante, que es secundario respecto al resultado (es decir al producto).

Se evalúa para dar una calificación. En esta enumeración, es la última de las razonas por las cuales se debe evaluar, pero ciertamente la de mayor difusión. Los alumnos deben por el contrario tener bien claro que evaluar no es sinónimo de dar una nota. Cuando se da una nota, se debe tener presente que:

• es necesario el uso de diversos instrumentos y técnicas, como lo veremos más adelante;

• es posible que el trabajo del estudiante sea diferente del trabajo usual cuando sabe que su trabajo será objeto de una calificación; y sin embargo los estudiantes deben saber con anticipación cuando un determinado trabajo que están por realizar será sometido a juicio;

• se requiere usar siempre un sistema de evaluación que tenga en cuenta tanto el proceso como el producto.

Las discusiones sobre los métodos y criterios de evaluación en matemática tienen raíces antiguas (en Jiménez Rodríguez, 1997 se ofrece una panorámica diacrónica y sincrónica de gran eficacia; véase también Fandiño Pinilla, 2002).

Consideramos necesario que sea claro que las modalidades concretas para realizar evaluaciones serias son muchísimas, no existen únicamente los cuestionarios o la solución de ejercicios o la resolución de problemas: hoy la investigación ha elaborado formas de evaluación sofisticadas, mucho más atendibles y significativas. Cuando llegue el momento, en el desarrollo de este libro, explicitaremos algunos de estos instrumentos.

En los apartados precedentes, privilegiemos la “evaluación para medir, para dar una calificación”. Pero no olvidemos que, como ya lo dijimos:

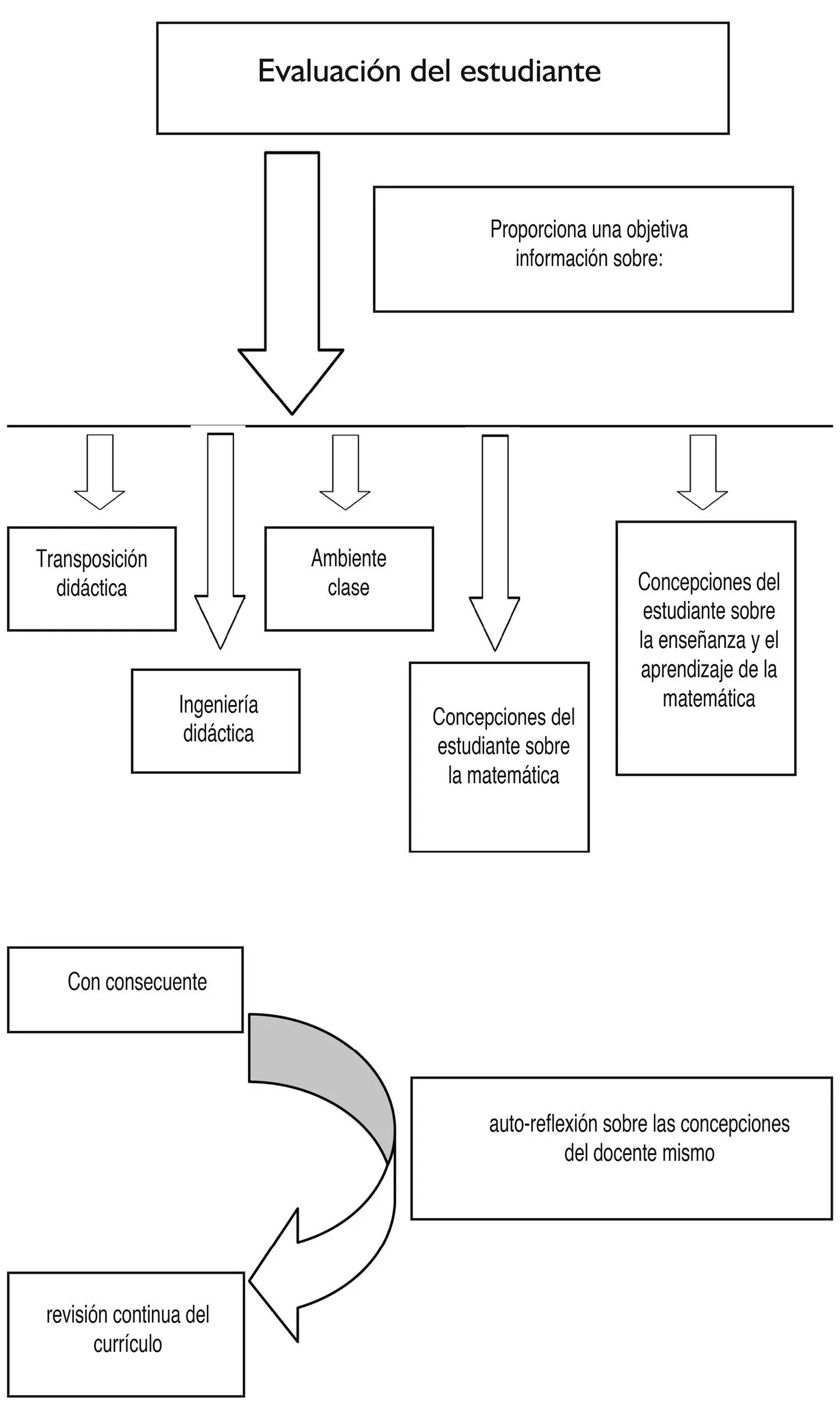
• se evalúa para tomar decisiones sobre el contenido (transposición didáctica) y sobre la metodología del trabajo en aula (ingeniería didáctica)

• se evalúa para tomar decisiones sobre el ambiente de clase

• se evalúa para comunicar a los alumnos lo que es importante,

como lo analizamos líneas arriba.

A través de oportunas técnicas de evaluación, el docente recibe informaciones claras sobre la eficacia de su acción didáctica en aula y por tanto de los contenidos tratados, de la metodología; obtiene además informaciones sobre el ambiente de clase; tiene la posibilidad, particularmente con pruebas que podemos llamar no tradicionales, de comunicar incluso explícitamente que es importante y que no lo es.

El análisis histórico de la evaluación, del sentido y de la función que le ha asignado la historia, de sus aspectos sociales etcétera, sería de gran interés, pero no es este el propósito de este libro; por lo tanto reenviamos a los textos enunciados precedentemente.

Así, existen varias teorías sobre la evaluación, teorías llamadas científicas, en sentido estricto, curricular, sobre las cuales invitamos a leer en los mismos textos citados precedentemente.

Precisamente, estas profundas reflexiones llevaron en el tiempo a establecer los criterios de tener presente en la evaluación, los métodos generales y específicos más adecuados, los instrumentos y sus funciones, el significado de validar los resultados que se obtienen con esta actividad.

Uno de los temas más interesantes es aquel de la relación entre convicciones de los docentes y evaluación; es obvio que diferentes convicciones impliquen diferentes evaluaciones. Pero, sobre todo esto, ya se hizo un profundo análisis por lo cual consideramos no sea necesario reportarlo aquí (Fandiño Pinilla, 2002).

Pero, una lectura como la que sigue, tiene sentido y es eficaz sólo si el docente que lee quiere hacer uso de los resultados reportados y si ya posee una buena capacidad crítica; deseamos aquí subrayar que, para nosotros, estas son las características de una innovación en la evaluación en matemática.

La forma más eficaz es la de hacer una breve lista de las condiciones que parecen determinar actualmente el sentido que tiene la innovación en la evaluación; lo haremos por puntos, buscando reutilizar algunos términos técnicos, evitando en lo posible largas explicaciones.

Las características principales de una innovación en la evaluación de un proceso sistemático de enseñanza - aprendizaje de la matemática, extrapoladas de los trabajos de investigación, son las siguientes:

• Una cuidadosa elección y descripción explícita de criterios y objetivos, con referencia a contenidos, en un modelo crítico - orientativo. Es así como la matemática debe ser considerada como una construcción significativa; la lista de los contenidos no es estática, por el contrario, ampliamente dinámica; debe ser incluida la valoración de los progresos locales de cada uno de los estudiantes; la elaboración de las actividades debe ser consecuencia del proceso o por lo menos relacionarse con este y no viceversa es decir fijada a priori de forma definitiva.

• La evaluación es vista como compleja y multidimensional, así como lo es el complejo proceso sistémico de enseñanza - aprendizaje.

• La evaluación no se restringe a un punto o a una cierta acción, por el contrario, debe ser realizada a lo largo de todo el arco del proceso de enseñanza - aprendizaje, dado que esta se considera una parte integrante de dicho proceso. La evaluación, por tanto, es continua y global.

• La evaluación debe ser adapta al estudiante evaluado y debe tener presente la diversidad. Evaluar significa también reconocer y aceptar las características individuales. La atención por la diversidad se extiende a la evaluación del currículo y del trabajo del docente.

• La evaluación implica el desarrollo de habilidades de tipo comunicativo. Esta favorece la adquisición de competencias incluso de tipo instrumental. El estudiante podrá desarrollar conceptos, procedimientos, actitudes y mejores estructuras, siempre que se mueva en esquemas no fijos, de forma tal que todo sea aplicable de forma independiente en las situaciones particulares; desde esta interpretación hablamos de “competencias estructurales”. El proceso de aprendizaje, entendido en un este vasto sentido, debe ser autorregulado; es decir favorecido de momentos de análisis crítico del proceso, replanteamientos y evaluaciones de carácter meta-cognitivo. En todo esto juega un papel esencial la explicitación, por parte del docente, de todo aquello que él piensa que deba suceder en el aula, en el proceso de enseñanza - aprendizaje y en el proceso de evaluación. Por último, se debe agregar la solicitud de claridad, con el objetivo de evitar ambigüedades sea en la asignación de las tareas, sea en la explicitación de las expectativas. Esto no debe entrar en contraposición con la idea de situación a-didáctica: no se debe confundir el contexto de enseñanza, es decir la elección de “buenas situaciones” de proponer para lograr los objetivos cognitivos, con las reflexiones sucesivas, o con la explicitación de los momentos de evaluación.