Martha Isabel Fandiño Pinilla - Múltiples aspectos del aprendizaje de la matemática

Sólo como ejemplo; junto a docentes de la escuela primaria hicimos una lectura específica de cada una de las componentes de la matemática de dicho nivel escolar, dado que se usaba identificar, hace algunos años, la matemática con el conjunto de componentes disciplinarios como números, figuras, medidas, datos y pensamiento racional (transversal), entonces cada una de dichas componentes disciplinarias puede ser analizada a través de las cinco componentes enunciadas líneas arriba y de proporcionar útiles indicaciones sobre como actuar didácticamente y como remediar a situaciones de fracaso en el aprendizaje.

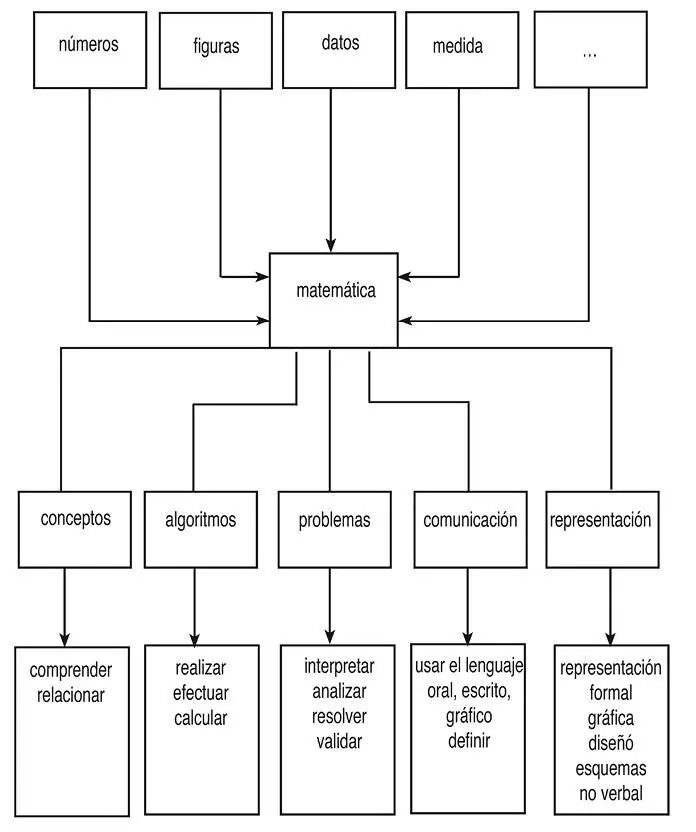
A continuación entraremos en detalle en cada una de estas componentes, una por capítulo, del capítulo 2 al 6. En este capítulo 1, pero, necesitamos aún de algunas consideraciones preliminares.

1.3. Saber y saber hacer: unicidad y diferencias

Iniciamos haciendo una distinción terminológica, muy discutida, sobre la cual es necesario aún reflexionar.

Saber. Hoy todos concordamos, por lo menos genéricamente, en el carácter “constructivo” del aprendizaje: aprender un concepto matemático, aprender a hacer uso de un algoritmo, a comportarse en modo estratégico, a comunicar la matemática y con la matemática,... son todos comportamientos a través de los cuales se construye un objeto matemático. El primer interprete de la construcción de un aprendizaje es quien lo construye; por tanto, una de las primeras acciones didácticas consiste en enseñar, en promover, en reflexionar sobre las propias estrategias personales, para percibirlas como propias, para evaluarlas. Quien está aprendiendo es el autor principal de su (propia) construcción de aprendizaje.

Saber hacer. Pero, consideramos que el saber por sí sólo, extrapolado de su contexto de uso, no llega a ser considerado saber, y esto vale no sólo para la matemática. Parece absolutamente necesario saber usar en contextos oportunos el concepto construido. El saber hacer sin el saber no es un saber, dado que carece del componente fundamental del saber, que es aplicativo y constructivo. Así, viceversa, el saber sin el saber hacer es vacío y estéril.

Para mayor claridad recurrimos a un ejemplo.

Aún admitiendo que existan sutiles diferencias entre un objeto como “recta” y uno como “demostración” y uno como “operación de división”, consideramos que en la fase de aprendizaje no haya, o no requiera, demasiadas distinciones; creemos que la operatividad (el llamado “saber hacer”) exija tanto del uso de conceptos, como de estrategias (el “saber resolver”,...) como de actividades algorítmicas (el “saber calcular”, el “saber operar”,...) etc.

Por tanto, el “saber” se mezcla con el “saber hacer” y sólo una sabia mezcla de estos tiene el derecho de ser llamado: aprendizaje consciente, saber.

Una antigua distinción que separaba el “saber” del “saber hacer” tiene el sabor de cosa superada, al menos en el campo específico del aprendizaje matemático en el cual el concepto no es nunca el concepto únicamente sino que incluye el uso que de este se hace a cualquier nivel.

A partir de este momento no se harán más distinciones entre “saber” y “saber hacer” pues estos dos aspectos se engloban en el saber mismo sin hacer diferencias.

1.4. Evaluar: un proceso

Una de las funciones que caracterizan con mayor fuerza la acción del docente en el aula es la constante “evaluación”; para decirlo brevemente, este proceso consta de por lo menos tres componentes distintas pero, aún una vez más, estrechamente relacionadas entre ellas (Fandiño Pinilla, 2002): evaluación

• de la propia acción didáctica

• del segmento curricular elegido y

• del proceso de aprendizaje de sus propios estudiantes.

Con relación con este último aspecto, el término “evaluación” se entiende aquí como el conjunto de las acciones mediante las cuales se reconocen las características del aprendizaje de los estudiantes y se determinan los aspectos en los cuales se debe centrar la ayuda que permite garantizar mejor este aprendizaje.

Obviamente dichas “acciones” conllevan un juicio sobre la eficacia de la propia acción didáctica y sobre el segmento curricular sobre el cual se está construyendo el aprendizaje.

En este marco de acción, el docente debe prestar atención a los instrumentos a través de los cuales mide el juicio de cada uno de los estudiantes, en relación con el aprendizaje de la matemática. No se puede y no se debe pensar en un único instrumento para esta evaluación; la investigación ha evidenciado la necesidad de hacer uso de varios y diversificados instrumentos.

Entrando con profundidad, analizamos adjetivos que, generalmente, se asocian al sustantivo “evaluación”.

Una distinción pedagógica que tuvo fortuna es aquella que concierne a la distinción entre evaluación “formativa”, “sumativa” y “evaluativa”; y que internacionalmente están definidas así (DES, 1987):

• la “evaluación formativa” toma en examen el desempeño de un estudiante en relación con sus objetivos cognitivos, en modo de favorecerla sobre la base de los resultados; se incluye en esta, por lo general, la “evaluación diagnóstica” en la cual se identifican las dificultades del estudiante, sea en lo relacionado con el aprendizaje, sea por lo que respecta la falta de comprensión;

• la “evaluación sumativa” mide y sintetiza las realizaciones del estudiante de forma sistemática; esta se reduce generalmente a un adjetivo, un número, una letra, y está destinada no sólo al estudiante y al docente, sino también al externo, a la familia, a la institución escolar;

• la “evaluación evaluativa” (que en español parece una repetición, pero que en inglés es llamada “evaluative assessment”) comprende una evaluación en relación con el trabajo del docente, sobre la escuela, sobre el currículo o sobre un parte de este,..., históricamente esta última tiene como mínimo las siguientes cuatro funciones (Cardinet, 1983):

– efectuar un balance sobre aquello que el estudiante está en grado de realizar en un determinado momento del proceso de enseñanza y aprendizaje;

– guiar la sucesiva fase del aprendizaje sobre la base del balance precedente (sea en relación con los contenidos, sea en relación con las metodologías);

– descubrir las causas de las dificultades del estudiante;

– estimular el éxito del estudiante, con el objetivo de encontrar la forma de favorecer el aprendizaje.

Una terna con significados deferentes del término “evaluación” aparece también en Frabboni (1999) quien distingue entre “predictiva”, “formativa” y “sumativa”; pero, a estas tres acepciones, que se refieren al estudiante, él agrega explícitamente una «evaluación de la escuela como sistema».

Respecto a estas tendencias “clásicas” de interpretar la idea misma de evaluación, el momento actual exige, cada vez con mayor fuerza, tener presente la didáctica de la matemática en la formación docente dado que ya son muchos los jóvenes docentes que entran en el mundo de la educación y docentes en servicio que han frecuentado cursos específicos de esta disciplina.

La disciplina “didáctica de la matemática” tiene por lo menos tres decenios de historia, un gran número de investigadores activos en el mundo, un lenguaje compartido, revista propias (tanto de investigación, como de divulgación, como “mixtas”), seminarios de investigación y de divulgación propios, congresos,..., lo cual hace que su difusión real sea cada vez más amplia.