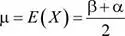Solución
Se tiene que:
p 1: Proporción muestral de hogares del distrito de Lince que poseen al menos un equipo de cómputo portátil
π 1= 0.25, n 1= 125
p 2: Proporción muestral de hogares del distrito de Jesús María que poseen al menos un equipo de cómputo portátil
π 2= 0.40, n 2= 120
Se sabe que: 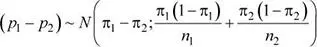
Entonces:
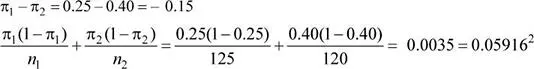
Se tiene que: ( p 1- p 2) ∼ N (-0.15;0.05916 2)
Luego, la probabilidad solicitada es: P (| p 1- p 2| < 0.05)
P (| p 1- p 2| < 0.05) = P (- 0.05 < p 1- p 2< 0.05) = 0.04512
20.En un estudio sobre el consumo de bebidas energizantes se determinó que el 40 % y 32 % de los jóvenes de los distritos de Santiago de Surco y La Molina, respectivamente, consumen algún tipo de bebida energizante. Suponga que se han seleccionado igual número de jóvenes de ambos distritos para que formen parte de la muestra en estudio. Si se ha calculado que existe una probabilidad de 0.63 de que la proporción muestral de jóvenes que consumen algún tipo de bebida energizante en el distrito de Santiago de Surco supere a la proporción correspondiente al distrito de La Molina en por lo menos 0.05. ¿Cuántos jóvenes fueron seleccionados en dichos distritos?
Solución
Se tiene que:
p 1: Proporción muestral de jóvenes del distrito de Santiago de Surco que consumen algún tipo de bebida energizante.
p 1: Proporción muestral de jóvenes del distrito de La Molina que consumen algún tipo de bebida energizante.
π 2= 0.32, n 2= ¿?
Se sabe que: 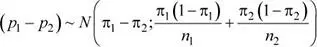
Entonces:
π 1− π 2= 0.40 − 0.32 = 0.08
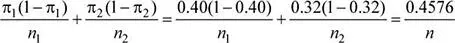
n 1= n 2= n
Se tiene que: 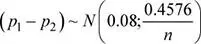
Además: 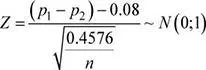
Se solicita calcular n , tal que: P ( p 1− p 2≥ 0.05) = 0.63

Por lo tanto: 
MISCELÁNEA DE PROBLEMAS
21.Con el objetivo de realizar un estudio, el Ministerio de la Producción revisó resultados anteriores donde se apreciaba lo siguiente: el tamaño de las truchas pescadas para consumo humano por parte de la pesca formal en el departamento de Junín presenta una distribución normal con una media de 26 cm y una desviación estándar de 2 cm.
a) Defina la variable de análisis asociada al presente caso.
X : Tamaño, en cm, de las truchas pescadas para consumo humano por parte de la pesca formal en el departamento de Junín.
b) Se desea analizar una muestra conformada por 26 truchas obtenidas por los pescadores formales, determine la probabilidad de que la desviación estándar de la muestra sea menor que 2.4 cm.
σ = 2 cm, n = 26
Se sabe que: 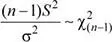
Luego, la probabilidad solicitada es: P ( S ≤ 2.4)
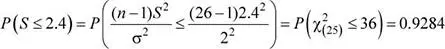
c) Se desea analizar otra muestra conformada por 32 truchas, determine la probabilidad de que el promedio muestral difiera de la media poblacional en menos de 0.5 cm.
μ = 26 cm, S = 2 cm, n = 32
Se sabe que: 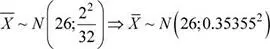
Luego, la probabilidad solicitada es:
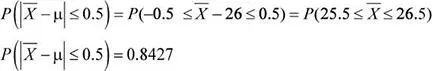
d) Escenario A. Uno de los resultados obtenidos en un estudio anterior se encontraba relacionado al número de infracciones leves que se han detectado a los pescadores formales durante inspecciones sorpresa en un determinado mes. Sobre la base de dichos resultados se elaboró la siguiente tabla de probabilidades:
| N° de infracciones leves |
Probabilidad |
| 0 |
0.04 |
| 1 |
0.60 |
| 2 |
0.30 |
| 3 |
0.06 |
Para el siguiente mes se han programado inspecciones sorpresa dirigidas a 44 pescadores formales seleccionados al azar. Determine la probabilidad de que la media muestral del número de infracciones leves sea menor que 1.5.
Media: 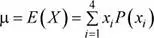
μ = 0(0.04) + 1(0.60) + 2(0.30) + 3(0.06) = 1.38 infracciones
Varianza: σ 2= E ( X 2) - [ E ( X )] 2
σ 2= [0 2(0.04) + 1 2(0.60) + 2 2(0.30) + 3 2(0.06)] - (1.38) 2
σ 2= 0.4356 infracciones 2
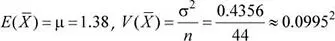
Aplicando el teorema central del límite:  ∼ N (1.38;0.0995 2)
∼ N (1.38;0.0995 2)
Luego, la probabilidad solicitada es: P (  ≤ 1.5) = 0.8861
≤ 1.5) = 0.8861
e) Escenario B. Otro resultado señalaba que el tiempo diario que los pescadores formales dedican a realizar sus actividades de pesca presenta una distribución uniforme de entre 240 y 320 minutos. Si se seleccionan al azar a 48 pescadores, ¿cuál es la probabilidad de que el tiempo total acumulado a las labores de pesca sea de por lo menos 230 horas?
X : Tiempo dedicado a las actividades de pesca por parte de los pescadores formales
X ∼ Uniforme (240;320)
Media: 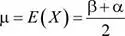
Читать дальше

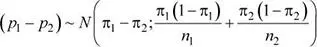
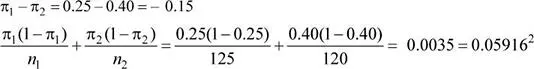
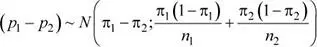
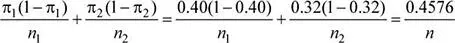
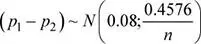
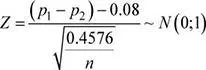


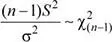
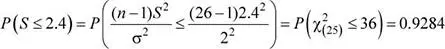
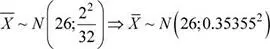
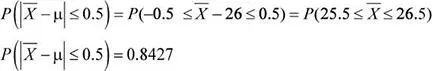
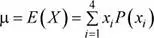
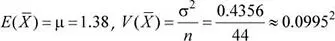
 ∼ N (1.38;0.0995 2)
∼ N (1.38;0.0995 2)