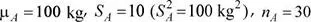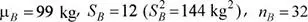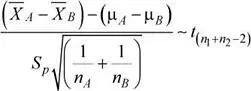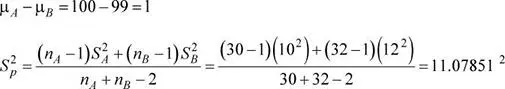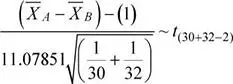Se tiene:
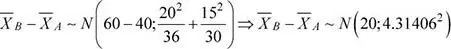
Luego, la probabilidad solicitada es:
P (  B−
B−  A> 25) = 0.1232
A> 25) = 0.1232
14.El jefe de producción de una empresa que se dedica a la fabricación de placas de policarbonato ha determinado que el grosor de las placas producidas en la máquina 1 presenta una distribución normal con media μ 1= 8.12 mm, mientras que las placas de la máquina 2 presentan una distribución normal con μ 2= 8.10 mm. Para el análisis se deben utilizar las siguientes desviaciones estándar muestrales: S 1= 0.06 mm y S 2= 0.05 mm. Se han seleccionado muestras aleatorias de 40 y 35 placas provenientes de las máquinas 1 y 2, respectivamente. Determine la probabilidad de que la media muestral de los grosores de las placas provenientes de la máquina 1 supere a la media muestral del grosor de las placas de la máquina 2. Suponga que las varian-zas poblacionales son homogéneas.
Solución
 1: Media muestral del grosor (en mm) de las placas de policarbonato producidas en la máquina 1.
1: Media muestral del grosor (en mm) de las placas de policarbonato producidas en la máquina 1.
μ 1= 8.12, S 1= 0.06, n 1= 40
 2: Media muestral del grosor (en mm) de las placas de policarbonato producidas en la máquina 2.
2: Media muestral del grosor (en mm) de las placas de policarbonato producidas en la máquina 2.
μ 2= 8.10, S 2= 0.05, n 2= 35
Se sabe que: 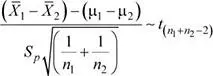
Entonces: 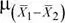
μ 1− μ 2= 8.12 − 8.10 = 0.02
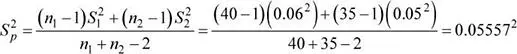
Se tiene que: 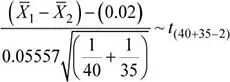
Luego, la probabilidad solicitada es: P (  1−
1−  2> 0
2> 0

15.Glasé es una empresa que produce galletas y dulces, en la planta de producción se ha determinado que la cantidad de masa procesada por hora, en las líneas de producción A y B, presentan distribuciones normales con medias μ A= 100 kg y μ A= 99 kg. Las varianzas poblacionales se desconocen pero se han estimado en 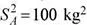 , y
, y 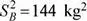 . Se han seleccionado, al azar, los registros de 30 y 32 horas de producción de las líneas A y B. Determine la probabilidad de que la media muestral de la cantidad de masa procesada por hora en la línea A sea mayor que la cantidad procesada en la línea B en a lo más un kilogramo. Suponga varianzas poblacionales homogéneas.
. Se han seleccionado, al azar, los registros de 30 y 32 horas de producción de las líneas A y B. Determine la probabilidad de que la media muestral de la cantidad de masa procesada por hora en la línea A sea mayor que la cantidad procesada en la línea B en a lo más un kilogramo. Suponga varianzas poblacionales homogéneas.
Solución
 A: Media muestral de la cantidad de masa procesada (kg) por hora en la línea A
A: Media muestral de la cantidad de masa procesada (kg) por hora en la línea A
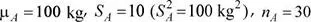
 B: Media muestral de la cantidad de masa procesada (kg) por hora en la línea B.
B: Media muestral de la cantidad de masa procesada (kg) por hora en la línea B.
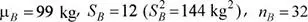
Se sabe que: 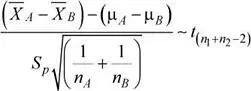
Entonces:
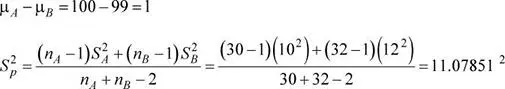
Se tiene que: 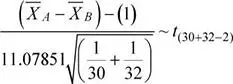
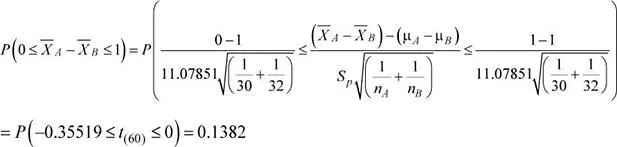
Luego, la probabilidad solicitada es: P (0 ≤  A−
A−  B≤ 1)
B≤ 1)
16.En el área de producción de una compañía industrial de equipos hidráulicos industriales, se prueba el funcionamiento de un tipo de válvulas de alta presión. Se determinó con anterioridad que el tiempo de prueba de dichas válvulas, en las plantas A y B, presentan distribuciones normales con varianzas poblacionales heterogéneas. Las desviaciones estándar se estimaron a partir de muestras aleatorias de tamaño 36 y 32, respectivamente. Los valores resumen de los datos que han sido utilizados para dicha estimación se presentan a continuación:

En muestras de tamaño similar, ¿cuál es la probabilidad de que la diferencia de las medias muestrales, en relación al tiempo de prueba de las válvulas, difiera en a lo más 2 segundos de la diferencia de las medias poblacionales correspondientes?
Solución
Se procede a calcular las varianzas muestrales

Se tiene que:
Читать дальше

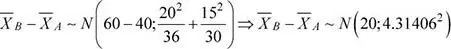
 B−
B− 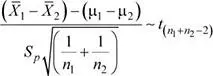
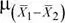
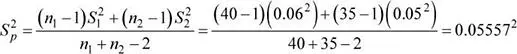
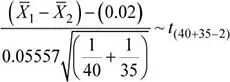

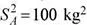 , y
, y 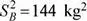 . Se han seleccionado, al azar, los registros de 30 y 32 horas de producción de las líneas A y B. Determine la probabilidad de que la media muestral de la cantidad de masa procesada por hora en la línea A sea mayor que la cantidad procesada en la línea B en a lo más un kilogramo. Suponga varianzas poblacionales homogéneas.
. Se han seleccionado, al azar, los registros de 30 y 32 horas de producción de las líneas A y B. Determine la probabilidad de que la media muestral de la cantidad de masa procesada por hora en la línea A sea mayor que la cantidad procesada en la línea B en a lo más un kilogramo. Suponga varianzas poblacionales homogéneas.