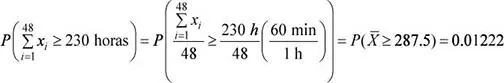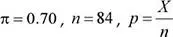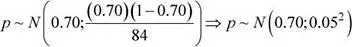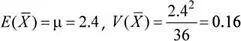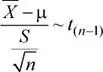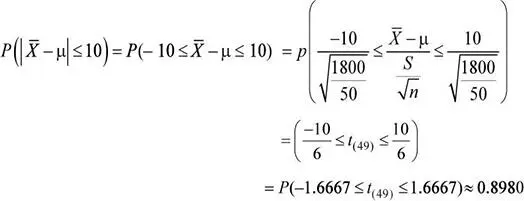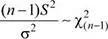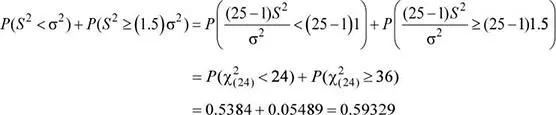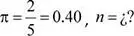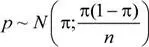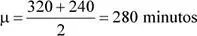
Varianza: 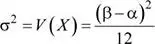
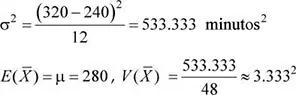
Aplicando el teorema central del límite:  ∼ N (280;3.333 2) Luego, la probabilidad solicitada es:
∼ N (280;3.333 2) Luego, la probabilidad solicitada es:
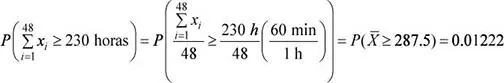
f) Escenario C. Se ha determinado que el 70 % de las ocasiones, los pescadores tienen una demanda que supera la pesca realizada. Para los próximos días se seleccionarán a 84 ocasiones de venta de los pescadores, ¿cuál es la probabilidad de que la proporción muestral difiera en por lo menos 0.08 de la proporción poblacional?
Solución
X : Número de ocasiones de venta, de las 84 seleccionadas, en que la demanda supera la pesca realizada.
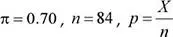
Se tiene que:
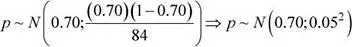
Luego, la probabilidad solicitada es: P ( p − π |≥ 0.08)
P (| p − π |≥ 0.08) = P (| p − 0.7|≥ 0.08) = P (| p − 0.7 ≤ -0.08) + P (| p − 0.7 ≥ 0.08) = P ( p ≤ 0.62) + P ( p ≥ 0.78) = 0.0548 + 0.0548 = 0.1096
22.Un regidor del distrito de Santiago de Surco se encuentra analizando diversos aspectos de la atención en plataforma, para lo cual se debe tener en cuenta lo siguiente:
• El tiempo transcurrido entre las inscripciones de bodas civiles no presenta una distribución normal.
• El tiempo de atención en la sección de tributos prediales presenta una distribución normal con una media 450 segundos y se estimó una varianza muestral S 2= 1800 seg 2.
• De acuerdo a los registros municipales se ha determinado que 2 de cada 5 solicitudes de licencias de funcionamiento son aprobadas en primera instancia.
a) Se ha señalado que el tiempo transcurrido entre inscripciones de bodas civiles presenta una distribución exponencial con media 2.4 horas. En base a una muestra de 36 bodas civiles, ¿cuál es la probabilidad de que la media muestral del tiempo transcurrido entre cada una de dichas inscripciones sea de a lo más 3.2 horas?
Solución
X : Tiempo, en horas, transcurrido entre la inscripción de bodas civiles
X ~ Exp (2.4)
Media: μ = E ( X ) = α = 2.4 horas
Varianza: σ 2= V ( X ) = 2.4 2horas 2
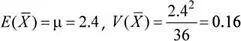
Aplicando el teorema central del límite:  ∼ N (2.4; 0.4) 2)
∼ N (2.4; 0.4) 2)
Luego, la probabilidad solicitada es: P (  ≤ 3.2)
≤ 3.2)
P (  ≤ 3.2) = 0.9772
≤ 3.2) = 0.9772
b) Se seleccionará una muestra de 50 usuarios atendidos en la sección de tributos prediales, calcule la probabilidad de que la media muestral de los tiempos de atención de los mencionados usuarios difiera a lo más en 10 segundos de su media poblacional.
Solución
 : Media muestral del tiempo de atención (seg) de los usuarios en la sección de tributos prediales
: Media muestral del tiempo de atención (seg) de los usuarios en la sección de tributos prediales
μ = 450 seg , S 2= 1800 seg 2, n = 50
Se sabe que: 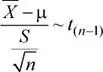
Luego, la probabilidad solicitada es: P (|  − μ| ≤ 10)
− μ| ≤ 10)
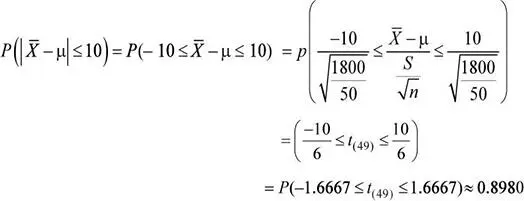
c) Después de un proceso de simplificación administrativa se determinó una nueva desviación estándar poblacional para el tiempo de atención en la sección de tributos prediales. Si se seleccionan 25 usuarios que son atendidos en la sección de tributos prediales, calcule la probabilidad de que la varianza muestral sea inferior o por lo menos 1.5 veces mayor a su varianza poblacional.
Solución
X : Tiempo de atención (en seg) de los usuarios en la sección de tributos prediales
n = 25
Se sabe que: 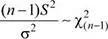
Luego, la probabilidad solicitada es: P ( S 2< σ 2) + P ( S 2≥ (1.5)σ 2)
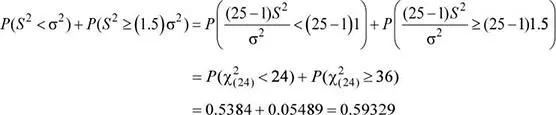
d) Se ha determinado que si se selecciona una muestra aleatoria de n solicitudes de licencias de funcionamiento, entonces la probabilidad de que la proporción muestral de las solicitudes aprobadas en primera instancia difiera de la proporción poblacional en a lo más 0.04 es de 0.6827. Determine el valor de n .
Solución
p : Proporción muestral de solicitudes de licencias que son aprobadas en primera instancia
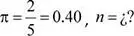
Se sabe que: 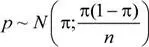
Luego,

Se solicita calcular n , tal que: P (| p – π | ≤ 0.04) = 0.6827
Читать дальше

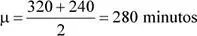
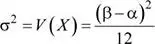
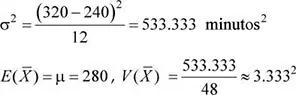
 ∼ N (280;3.333 2) Luego, la probabilidad solicitada es:
∼ N (280;3.333 2) Luego, la probabilidad solicitada es: