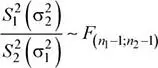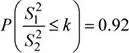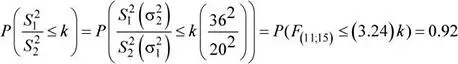1: Media muestral del tiempo de prueba de las válvulas en la Planta A
1: Media muestral del tiempo de prueba de las válvulas en la Planta A
S 1= 9, n 1= 36
 2: Media muestral del tiempo de prueba de las válvulas en la Planta B
2: Media muestral del tiempo de prueba de las válvulas en la Planta B
S 2= 10.5, n 2= 32
Se sabe que: 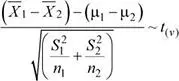
Los grados de libertad ( v ) se determinan a partir de la siguiente fórmula:
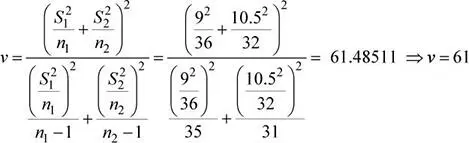
Además:
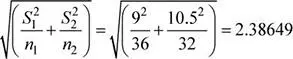
Se tiene que: 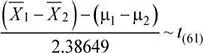
Luego, la probabilidad solicitada es: 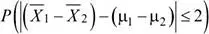
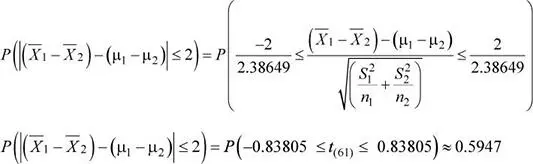
Distribución del cociente de varianzas muestrales 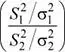
17.En una agencia de seguros se está analizando el tiempo de duración de las entrevistas, en minutos, con los potenciales empleados de una nueva sede. De registros anteriores se sabe que los tiempos de duración de las entrevistas, en minutos, realizadas por los especialistas 1 y 2 presentan las siguientes distribuciones normales: N (18;2.0 2) y N (16;2.5 2), respectivamente. Se seleccionan dos muestras aleatorias independientes de tamaños 30 y 36 entrevistas realizadas por los especialistas 1 y 2, respectivamente. Calcule la probabilidad de que la varianza muestral de los tiempos de entrevistas realizadas por el Especialista 1 sea inferior a la varianza de los tiempos de entrevista del Especialista 2.
Solución
Se tiene que:
X 1: Tiempo de duración de las entrevistas realizadas por el Especialista 1.
σ 1= 2.0 minutos, n 1= 30
X 2: Tiempo de duración de las entrevistas realizadas por el Especialista 2.
σ 2= 2.5 minutos, n 2= 36
Se sabe que: 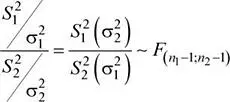
Se tiene que: 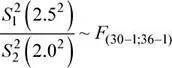
Luego, la probabilidad solicitada es: 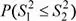
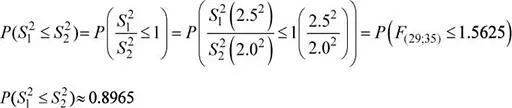
18.Nature es una empresa que se dedica al procesamiento y comercialización de frutos secos. El gerente general se encuentra interesado en analizar diversos aspectos de las actividades de comercialización de la empresa, para lo cual se dispone de la siguiente información relacionada con la cantidad, en kilogramos, de castañas de calidad extra solicitadas en cada pedido por parte de los dos principales clientes de la empresa: Kredy y Zegal.
| Variable |
Información |
| Cantidad de castañas de calidad extra solicitadas en cada pedido realizado por la empresa Kredy. |
Normal |
μ 1= 240 kg σ 1= 20 kg |
| Cantidad de castañas de calidad extra solicitadas en cada pedido realizado por la empresa Zegal. |
Normal |
μ 2= 225 kg σ 2= 36 kg |
a) Se seleccionan dos muestras aleatorias conformadas por 12 y 16 pedidos realizados por las empresas Kredy y Zegal, respectivamente, ¿cuál es la probabilidad de que la desviación estándar muestral de la cantidad de castañas extras solicitadas en los pedidos de la empresa Kredy a lo más sea la mitad de la desviación estándar muestral asociada a la empresa Zegal?
Solución
Se tiene que: 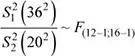
Luego, la probabilidad solicitada es: P ( S 1≤ (0.5) S 2)
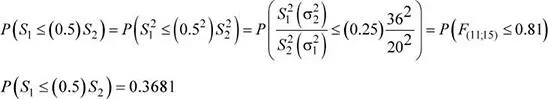
b) Sobre la base de los mismos tamaños de muestra del ítem anterior, existe una probabilidad de 0.92 de que la razón de varianzas muestrales 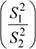 no exceda el valor k . Determine el valor de k .
no exceda el valor k . Determine el valor de k .
Solución
Se tiene que:
X 1: Cantidad, en kg, de castañas extra solicitadas por la empresa Kredy.
σ 1= 20 kg, n 1= 12
X 2: Cantidad, en kg, de castañas extra solicitadas por la empresa Zegal.
σ 2= 36kg, n 2= 16
Se sabe que: 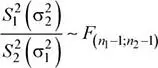
El valor de k solicitado verifica la siguiente relación: 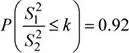
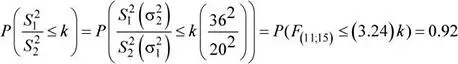
Luego: 3.24( k ) = 2.185 ⇒ k = 0.67438
Distribución de la diferencia de proporciones muestrales( p 1– p 2)
19.Según un estudio relacionado con el uso de tecnología en los hogares se determinó que el 25 % de los hogares del distrito de Lince poseen al menos un equipo de cómputo portátil ( laptop , notebook o ultrabook ), mientras que el 40 % de los hogares del distrito de Jesús María poseen al menos un equipo de cómputo portátil. Suponga que se seleccionan 125 y 120 hogares de los distritos de Lince y Jesús María, respectivamente. ¿Cuál es la probabilidad de que la proporción muestral de hogares del distrito de Lince que poseen al menos un equipo de cómputo portátil difiera de la proporción muestral del distrito de Jesús María en menos de 0.05?
Читать дальше

 1: Media muestral del tiempo de prueba de las válvulas en la Planta A
1: Media muestral del tiempo de prueba de las válvulas en la Planta A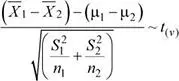

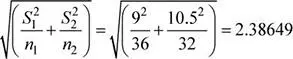
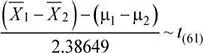
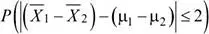
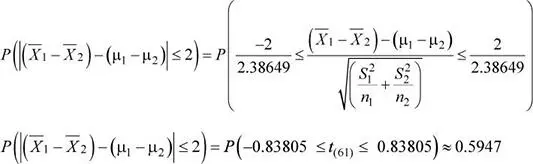
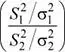
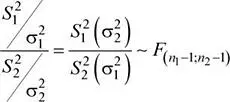
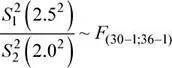
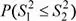
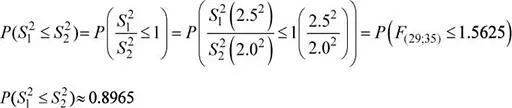
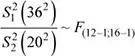
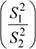 no exceda el valor k . Determine el valor de k .
no exceda el valor k . Determine el valor de k .