
Para hallar la probabilidad, mediante el gráfico de probabilidad, se usará la probabilidad de las colas simétricas (1 – 0.6827 = 0.3173) y no la del cuerpo central.
Por lo tanto: 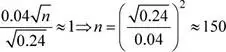
f) Escenario A. De los registros se ha determinado que los tiempos de atención a las solicitudes de licencias de funcionamiento, en horas de procesamiento administrativo, de solicitudes realizadas en la oficina principal (P) o en la oficina descentralizada (D), se distribuyen normalmente con varianzas poblacionales desconocidas, pero iguales. Se dispone de la siguiente información de interés:
μ P= 38.4 h , S P = 4.8 h , m D = 40.0 h , s D = 4.4
Se han seleccionado muestras aleatorias de 40 y 39 solicitudes de licencias de funcionamiento en la oficina principal y en la descentralizada, respectivamente, y se ha calculado una probabilidad de 0.06 de que la media muestral del tiempo de atención a las solicitudes en la oficina principal supere a la media muestral de la oficina descentralizada en por lo menos k horas. ¿Cuál es el valor de k ?
Solución
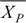 : Media muestral del tiempo (horas) de atención a las solicitudes de licencias de funcionamiento en la oficina principal.
: Media muestral del tiempo (horas) de atención a las solicitudes de licencias de funcionamiento en la oficina principal.
μ P = 38.4 h , S P = 4.8 h , n P = 40
 D : Media muestral del tiempo (horas) de atención a las solicitudes de licencias de funcionamiento en la oficina descentralizada.
D : Media muestral del tiempo (horas) de atención a las solicitudes de licencias de funcionamiento en la oficina descentralizada.
μ D= 40.0 h , S D = 4.4 h , n D = 39
Se sabe que: 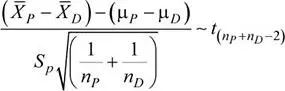
Entonces: 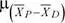 = μ P− μ D38.4 – 40.0 = – 1.6
= μ P− μ D38.4 – 40.0 = – 1.6
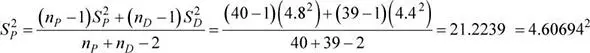
Se tiene que:
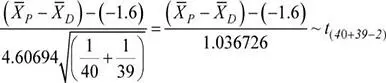
El valor de k solicitado verifica la siguiente relación: P (  1−
1−  2≥ k ) = 0.06
2≥ k ) = 0.06

f) Escenario B.En la oficina principal se ha determinado que el 20 % de las atenciones en plataforma corresponden a los vecinos de la Zona 01 del distrito, mientras que en la oficina descentralizada el 32 % de las atenciones corresponden a los vecinos de dicha zona. Si se seleccionan al azar muestras de 38 y 42 atenciones realizadas en la oficina principal y la descentralizada, respectivamente, determine la probabilidad de que la proporción muestral de las atenciones correspondientes a los vecinos de la Zona 01 en la oficina principal supere en a lo más 0.05 a la proporción muestral de las atenciones correspondientes a los vecinos de la Zona 01 en la oficina descentralizada.
Solución
p 1: Proporción muestral de las atenciones correspondientes a los vecinos de la Zona 01 del distrito (oficina principal) π 1= 0.20, n 1= 38
p 2: Proporción muestral de las atenciones correspondientes a los vecinos de la Zona 01 del distrito (oficina descentralizada). π 2= 0.32, n 2= 42
Se sabe que:
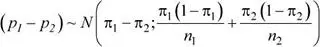
Entonces:
π 1− π 2= 0.20 − 0.32 = −0.12
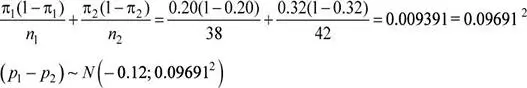
Calcular:
P (0 ≤ p 1− p 2≤ 0.05) = 0.06811
23.Una revista orientada al público joven se encuentra realizando un estudio sobre el uso de los smartphones y tablets para conectarse a Internet, por parte de los jóvenes de Lima metropolitana que poseen dichos dispositivos. Se había determinado que el tiempo de uso diario de los smartphones presenta una distribución normal con media μ 1= 108 min y σ 1= 16 min, mientras que el tiempo de uso diario de las tablets presenta una distribución normal con μ 2= 115 min y σ 2= 21 min.
a) Si se seleccionan dos muestras aleatorias de 32 y 35 jóvenes que poseen smartphones y tablets , respectivamente, calcule la probabilidad de que la media muestral del tiempo de uso diario de los smartphones sea inferior a la media muestral del tiempo de uso diario de las tablets .
Solución
 1: Media muestral del tiempo (min) de uso diario de los smartphones para conectarse a Internet. μ 1= 108 min, σ 1= 16 min, n 1= 32
1: Media muestral del tiempo (min) de uso diario de los smartphones para conectarse a Internet. μ 1= 108 min, σ 1= 16 min, n 1= 32
 2: Media muestral del tiempo (min) de uso diario de las tablets para conectarse a Internet. μ 2= 115 min, σ 2= 21 min, n 2= 35
2: Media muestral del tiempo (min) de uso diario de las tablets para conectarse a Internet. μ 2= 115 min, σ 2= 21 min, n 2= 35
Se sabe que: 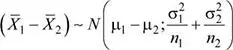
Se tiene que
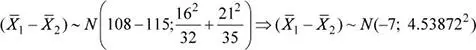
Luego, la probabilidad solicitada es: P (  1−
1−  2≤ 0) = 0.9385
2≤ 0) = 0.9385
b) Escenario A.La cantidad de música, en gigabytes (GB), almacenada en los smartphones por parte de los jóvenes de 15 a 19 años, y de los jóvenes de 20 a 24 años, presentan distribuciones normales con medias μ 1= 3.60 y μ 2= 3.35, respectivamente. Las varianzas poblacionales se desconocen pero se han estimado: 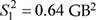 y
y 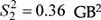 . Si se selecciona 2 muestras aleatorias de 42 y 38 jóvenes de 15 a 19, y de 20 a 24 años, respectivamente, calcule la probabilidad de que la media muestral de la cantidad de música almacenada en los smartphones por parte de los jóvenes de 15 a 19 años supere entre 0.50 y 0.75 GB la música almacenada por los jóvenes de 20 a 24 años. Suponga varianzas poblacionales homogéneas.
. Si se selecciona 2 muestras aleatorias de 42 y 38 jóvenes de 15 a 19, y de 20 a 24 años, respectivamente, calcule la probabilidad de que la media muestral de la cantidad de música almacenada en los smartphones por parte de los jóvenes de 15 a 19 años supere entre 0.50 y 0.75 GB la música almacenada por los jóvenes de 20 a 24 años. Suponga varianzas poblacionales homogéneas.
Читать дальше


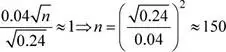
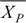 : Media muestral del tiempo (horas) de atención a las solicitudes de licencias de funcionamiento en la oficina principal.
: Media muestral del tiempo (horas) de atención a las solicitudes de licencias de funcionamiento en la oficina principal. D : Media muestral del tiempo (horas) de atención a las solicitudes de licencias de funcionamiento en la oficina descentralizada.
D : Media muestral del tiempo (horas) de atención a las solicitudes de licencias de funcionamiento en la oficina descentralizada.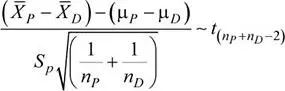
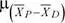 = μ P− μ D38.4 – 40.0 = – 1.6
= μ P− μ D38.4 – 40.0 = – 1.6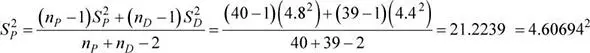
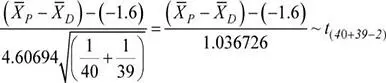

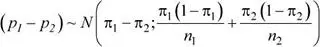
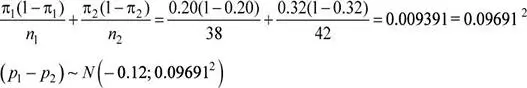
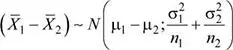
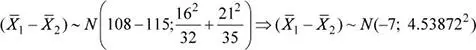
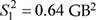 y
y 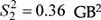 . Si se selecciona 2 muestras aleatorias de 42 y 38 jóvenes de 15 a 19, y de 20 a 24 años, respectivamente, calcule la probabilidad de que la media muestral de la cantidad de música almacenada en los smartphones por parte de los jóvenes de 15 a 19 años supere entre 0.50 y 0.75 GB la música almacenada por los jóvenes de 20 a 24 años. Suponga varianzas poblacionales homogéneas.
. Si se selecciona 2 muestras aleatorias de 42 y 38 jóvenes de 15 a 19, y de 20 a 24 años, respectivamente, calcule la probabilidad de que la media muestral de la cantidad de música almacenada en los smartphones por parte de los jóvenes de 15 a 19 años supere entre 0.50 y 0.75 GB la música almacenada por los jóvenes de 20 a 24 años. Suponga varianzas poblacionales homogéneas.










