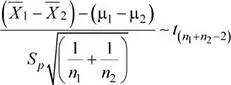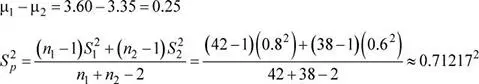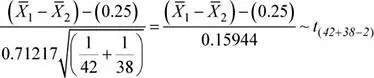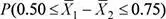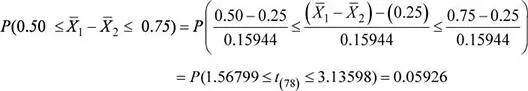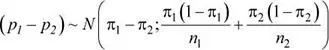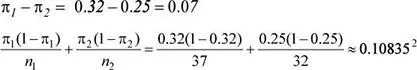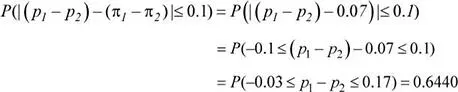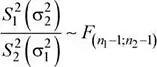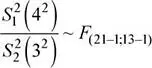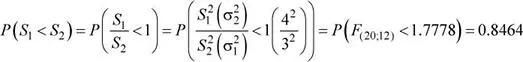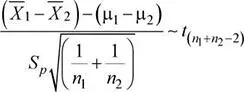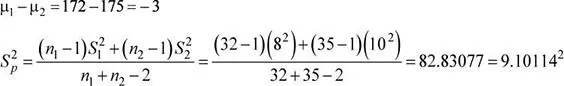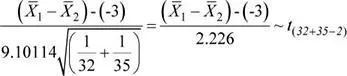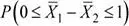Solución
 1: Media muestral de la cantidad (GB) de música almacenada en smartphones por parte de los jóvenes de 15–19 años μ 1= 3.60 GB , S 1= 0.8 GB , n 1= 42
1: Media muestral de la cantidad (GB) de música almacenada en smartphones por parte de los jóvenes de 15–19 años μ 1= 3.60 GB , S 1= 0.8 GB , n 1= 42
 2: Media muestral de la cantidad (GB) de música almacenada en smartphones por parte de los jóvenes de 20–24 años μ 2= 3.35 GB , S 2= 0.6 GB , n 2= 38
2: Media muestral de la cantidad (GB) de música almacenada en smartphones por parte de los jóvenes de 20–24 años μ 2= 3.35 GB , S 2= 0.6 GB , n 2= 38
Se sabe que: 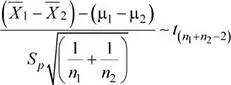
Entonces:
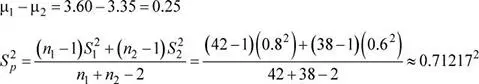
Se tiene que:
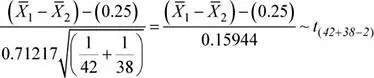
Luego, la probabilidad solicitada es: 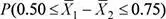
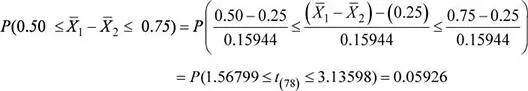
c) Escenario B.Se ha determinado que de los jóvenes de 20 a 24 años el 32 % poseen smartphones de última generación; mientras que de los jóvenes de 15 a 19 años el 25 % poseen smartphones de última generación. Si se selecciona 2 muestras aleatorias de 37 y 32 jóvenes de 20 a 24 y 15 a 19 años, respectivamente, calcule la probabilidad de que la diferencia de proporciones muestrales de jóvenes de 20 a 24 años y de 15 a 19 años que poseen smartphones de última generación difiera en a lo más 0.10 de la correspondiente diferencia de proporciones poblacionales.
Solución
p 1: Proporción muestral de jóvenes de 20 a 24 años que poseen smartphones de última generación π 1= 0.32, n 1= 37
p 2: Proporción muestral de jóvenes de 15 a 19 años que poseen smartphones de última generación π 2= 0.25, n 2= 32
Se sabe que:
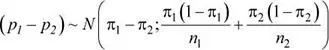
Entonces:
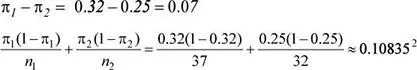
Se tiene que: ( p 1− p 2) ∼ N (0.07;0.10835 2)
Luego, la probabilidad solicitada es: P (|( p 1− p 2) – ( π 1– π 1) |≤ 0.1)
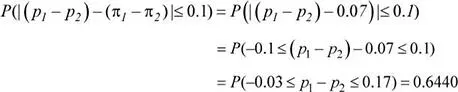
24.El Departamento de Sistemas de una empresa consultora desea comparar dos paquetes de software para el procesamiento de proyectos de Data Mining. Estos proyectos requieren del manejo de un gran volumen de datos, cuyo procesamiento consume gran cantidad de tiempo, dependiendo del volumen de los datos. Suponga que el tiempo de procesamiento de un proyecto de Data Mining estándar empleado por el software A es una variable aleatoria normal con media 54 minutos y desviación estándar 3 minutos, mientras que con el software B el tiempo de procesamiento tiene una distribución normal con media 52 minutos y desviación estándar 4 minutos. El ingeniero encargado de la evaluación de los paquetes de software ejecutará 21 veces el software A y 13 veces el software B.
a) Calcule la probabilidad de que la desviación estándar muestral de los tiempos de procesamiento obtenidos con el software A sea menor que la desviación estándar muestral obtenida con el software B.
Solución
X 1: Tiempo de procesamiento, minutos, aplicando el software A
μ 1= 54 min, S 1= 3 min, n 1= 21
X 1: Tiempo de procesamiento, minutos, aplicando el software B.
μ 2= 52 min, S 2= 4 min, n 2= 13
Se sabe que: 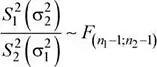
Se tiene que: 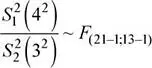
Se solicita calcular: P ( S 1< S 2)
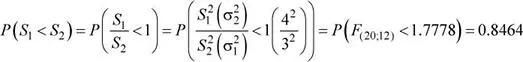
b) Escenario A.Otro de los aspectos de evaluación se refiere al tiempo necesario para la adecuación de los datos al formato de ingreso en los mencionados paquetes de software. Para esta evaluación se ha decidido adecuar bases de datos de por lo menos 5000 registros y 20 columnas. Se sabe lo siguiente: el tiempo de adecuación de los datos para el ingreso en el software A presenta una distribución normal con media 172 seg y con una varianza desconocida pero estimada en 64 seg 2; mientras que el tiempo de adecuación de los datos para el ingreso en el software B presenta una distribución normal con media 175 seg y con una varianza desconocida pero estimada en 100 seg 2. Si se realizan pruebas con 32 y 35 bases de datos para el software A y B, respectivamente, determine la probabilidad de que la media muestral del tiempo de adecuación de datos para el software A supere a la media muestral del software B en a lo más 1 segundo. Suponga que las varianzas poblacionales son homogéneas.
Solución
 1: Media muestral del tiempo (en seg) de adecuación de datos para software A μ 1= 172 seg , S 1= 8 seg , n 1= 32
1: Media muestral del tiempo (en seg) de adecuación de datos para software A μ 1= 172 seg , S 1= 8 seg , n 1= 32
 2: Media muestral del tiempo (en seg) de adecuación de datos para software B
2: Media muestral del tiempo (en seg) de adecuación de datos para software B
μ 2= 175 seg , S 2= 10 seg , n 2= 35
Se sabe que: 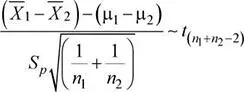
Entonces:
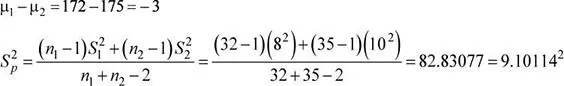
Se tiene que:
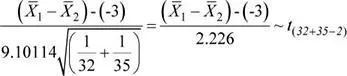
Luego, la probabilidad solicitada es: 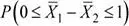
Читать дальше

 1: Media muestral de la cantidad (GB) de música almacenada en smartphones por parte de los jóvenes de 15–19 años μ 1= 3.60 GB , S 1= 0.8 GB , n 1= 42
1: Media muestral de la cantidad (GB) de música almacenada en smartphones por parte de los jóvenes de 15–19 años μ 1= 3.60 GB , S 1= 0.8 GB , n 1= 42