1 ...6 7 8 10 11 12 ...26 Die 84 Probleme des Papyrus Rhind illustrieren damalige mathematische Methoden. So fragt Problem 24, welche Zahl, wenn man sie zu ihrem siebten Teil addiert, 19 ergibt. Als Gleichung ist dies x + x/ 7= 19. Das angegebene Lösungsprinzip nennt man heute Regula-falsi -Methode (Latein: »Regel des Falschen«). Sie war bis ins Mittelalter verbreitet und basiert auf Versuch und Annäherung: Man wählt einen »falschen« Wert (»Ansatz«) für die Variable und nähert ihn dann durch Multiplikation mit einer Zahl (tatsächliches Ergebnis geteilt durch falsches Ergebnis) an.
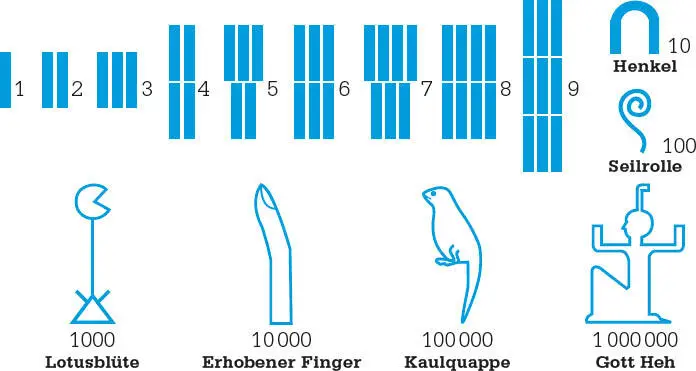
Die alten Ägypterrepräsentierten die Zahlen 1 bis 9 mit vertikalen Strichen. Zehnerpotenzen, vor allem in Steininschriften, wurden als Hieroglyphen (Bildsymbole) dargestellt.
In Problem 24 ist ein Siebtel einfach für die Zahl 7 zu berechnen, also wählt man 7 als »Ansatz« für x . Das Ergebnis, 7 + 7/ 7, ist 8 statt 19. Um herauszufinden, wie weit man vom richtigen Wert entfernt ist, berechnet man Folgendes: 19 geteilt durch 8. Das ergibt 2 3/ 8, notiert als 2 + ¼ + 1/ 8. Nun muss man den ursprünglichen, »falschen« Ansatz (7) mit dieser Zahl multiplizieren, was x = 16 5/ 8bzw. 16 + ½ + 1/ 8ergibt. Damit hat man bereits die Lösung gefunden: 16 5/ 8+ (16 5/ 8) : 7 = 19.
Viele Probleme des Papyrus handeln von Waren oder Ländereien. Problem 41 berechnet das Volumen eines zylindrischen Getreidespeichers mit einem Durchmesser von 9 Meh (Ellen) und einer Höhe von 10 Meh . Dazu findet man die Fläche eines Quadrats mit einer Seitenlänge von 8/ 9des Durchmessers und multipliziert sie mit der Höhe. Denn ein Kreis mit Durchmesser 9 hat etwa die gleiche Fläche wie ein Quadrat mit Seitenlänge 8. Dies wird auch in Problem 50 zur Berechnung der Fläche eines Kreises genutzt: Ziehe 1/ 9vom Kreisdurchmesser ab und berechne die Fläche des Quadrats mit der resultierenden Seitenlänge.
Seit der griechischen Antike berechnet man die Fläche A eines Kreises, indem man das Quadrat des Radius ( r 2) mit der Zahl Pi ( π ) multipliziert, also A = πr 2. Die Ägypter hatten kein Konzept von Pi, aber der Papyrus Rhind zeigt, dass sie dem Wert schon sehr nahe kamen. Die Kreisflächenberechnung lässt sich als ( 8/ 9· 2 r ) 2ausdrücken (der Durchmesser ist der doppelte Radius), also 256/ 81· r 2, was effektiv einen Wert für Pi von 256/ 81ergibt. Das ist nur 0,6 % größer als der wahre Wert von Pi. 
Lehrbücher
Die Papyri Rhind und Moskau 4676 sind die am vollständigsten erhaltenen mathematischen ägyptischen Texte. Sie entstanden im bzw. kurz nach dem Mittleren Reich. Schreiber, die sich gut mit Arithmetik, Geometrie und Messwesen auskannten, kopierten sie sorgfältig. Man verwendete die Texte wohl als Übungen in Schreiberschulen. Zwar gaben diese vermutlich den höchsten Stand der Mathematik wieder, galten damals aber nicht als Wissenschaftswerke. Vielmehr waren es Handbücher für Handel, Buchhaltung, Bauwesen und andere Tätigkeiten, bei denen man messen und rechnen musste.
Baumeister nutzten Mathematik etwa beim Pyramidenbau. Der Papyrus Rhind zeigt die Berechnung einer Neigung mit der Einheit Seked – dem horizontalen Abstand (in Handbreiten), bei dem eine geneigte Linie um 1 Meh (Königselle: 52,4 cm) abfällt. Je steiler die Pyramidenseite sein sollte, desto weniger Seked musste man abmessen.
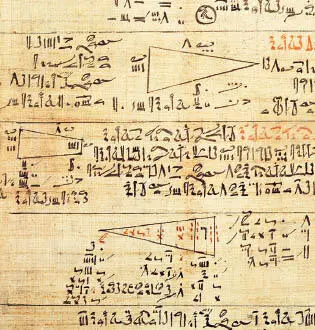
Der Autor des Papyrus Rhindverwendete die hieratischen Schrift- und Zahlzeichen. Dieser kursive Schreibstil war kompakter und praktischer als Hieroglyphen.

GLEICHE SUMME IN ALLE RICHTUNGEN
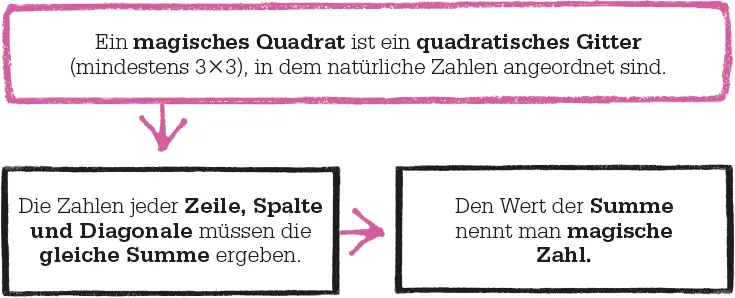
MAGISCHE QUADRATE
IM KONTEXT
SCHLÜSSELZIVILISATION
Altes China
TEILGEBIET
Zahlentheorie
FRÜHER
9. Jh. v. Chr.Das chinesische I Ging ( Yijing , »Buch der Wandlungen«) enthält Trigramme und Hexagramme zur Verwendung in Orakeln.
SPÄTER
1782Leonhard Euler schreibt über lateinische Quadrate in dem 155-seitigen Recherches sur une nouvelle espèce de quarrés magiques in einer niederländischen Zeitschrift.
1979Das erste Sudoku-ähnliche Rätsel wird in New York von Dell Magazines gedruckt.
2001Der britische Elektronikingenieur Lee Sallows erfindet »geomagische Quadrate«: magische Quadrate, die geometrische Formen statt Zahlen enthalten.
Es gibt Hunderttausende Wege, die Zahlen 1 bis 9 in einem 3×3-Gitter zu verteilen. Nur acht ergeben ein magisches Quadrat, in dem die Summe jeder Zeile, Spalte und Diagonale den gleichen Wert – die magische Zahl – hat. Die Summe der Zahlen von 1 bis 9 ist 45, daher ist sie auch die Summe der drei Spalten bzw. Zeilen. Die magische Zahl ist demnach 1/ 3von 45, also 15. Tatsächlich gibt es aber nur ein einziges magisches 3×3-Quadrat, da die anderen sieben nur Drehungen davon sind.
Magische Quadrate sind wohl das früheste Beispiel für »Unterhaltungsmathematik«. Ihr genauer Ursprung ist unbekannt, die erste dokumentierte Erwähnung ist die chinesische Legende Lo Shu (»Schriftrolle des Flusses Lo«) von 650 v. Chr. Darin erscheint eine Schildkröte vor dem König Yu, als eine gefährliche Überschwemmung droht. Die Zeichen auf ihrem Panzer bilden ein magisches Quadrat. Dabei stehen Punkte für die Zahlen 1 bis 9. Aufgrund dieser Legende galt die Anordnung von ungeraden und geraden Zahlen (gerade Zahlen standen stets in den Ecken) als magisch und wurde als Glücksbringer verwendet.
Chinesisches Wissen breitete sich entlang der Seidenstraße aus, und andere Kulturen begannen, sich für magische Quadrate zu interessieren. Indische Texte erwähnen sie ab 100 n. Chr. und die erste dokumentierte Darstellung im Wahrsagebuch Brihat-Samhita (um 550 n. Chr.) misst Parfüm damit ab. Arabische Gelehrte, die eine wichtige Verbindung zwischen dem Wissen der Antike und der europäischen Renaissance bildeten, brachten im 14. Jahrhundert magische Quadrate nach Europa.

Ein magisches Quadrat vierter Ordnungunter der Glocke im Kupferstich Melencolia I des Nürnberger Künstlers Albrecht Dürer enthält auch das Entstehungsjahr des Werks, 1514.
Die Anzahl der Zeilen und Spalten eines magischen Quadrats nennt man die Ordnung: Ein 3×3-Quadrat hat die Ordnung 3. Ein magisches Quadrat der Ordnung 2 gibt es nicht, denn darin müssten alle Zahlen gleich sein. Mit zunehmender Ordnung gibt es immer mehr Möglichkeiten. So gibt es 880 magische Quadrate der Ordnung 4 (ohne Drehungen und Spiegelungen), ihre magische Zahl ist 34. Mit der Ordnung 5 gibt es Hunderte von Millionen magische Quadrate, und die Zahl der Ordnung 6 ist noch unbekannt.
Читать дальше


















