Im Zahlensystem der Maya repräsentierte ein Punkt 1 und ein Strich 5. Kombinationen von Punkten über Strichen ergaben Zahlzeichen bis 19. Größere Zahlen ab 20 schrieb man mit mehreren Stellen vertikal untereinander, wobei die unterste Ziffer den geringsten Wert hatte. So rechneten sie wohl bis in die hundert Millionen. Eine Inschrift von 36 v. Chr. zeigt erstmals eine Muschel als Symbol für die Null, das ab dem 4. Jahrhundert weit verbreitet war.
Die Maya-Zahlschrift wurde in Mittelamerika bis zur spanischen Eroberung im 16. Jahrhundert verwendet, doch sie breitete sich nicht weiter aus.

Der Dresdner Kodex aus dem 13. Jh., die wohl älteste der vier authentischen Maya-Handschriften, zeigt Zahlensymbole und Glyphen.
DAS QUADRAT ALS HÖCHSTE POTENZ
QUADRATISCHE GLEICHUNGEN
IM KONTEXT
SCHLÜSSELZIVILISATIONEN
Ägypter(um 2000 v. Chr.),
Babylonier(um 1600 v. Chr.)
TEILGEBIET
Algebra
FRÜHER
um 1800 v. Chr.Der Papyrus Berlin 6619 zeigt die Lösung einer quadratischen Gleichung aus dem alten Ägypten.
SPÄTER
7. Jh. n. Chr.Der Inder Brahmagupta findet positive ganzzahlige Lösungen für einige quadratische Gleichungen.
10. Jh. n. Chr.Der Ägypter Abu Kamil Schudscha ibn Aslam löst quadratische Gleichungen mit negativen und irrationalen Zahlen.
1545Der italienische Arzt und Mathematiker Gerolamo Cardano beschreibt in Ars Magna algebraische Regeln.
Quadratische Gleichungen beinhalten eine unbekannte Zahl (meist x geschrieben), die als zweite Potenz (quadratisch: x 2) vorkommt, aber nicht als höhere Potenz: x 3, x 4usw. Ein Nutzen der Mathematik ist, mit Gleichungen Probleme der realen Welt zu lösen. Geht es um Flächen oder bestimmte Kurven wie Parabeln, sind quadratische Gleichungen nützlich und beschreiben physikalische Phänomene wie etwa die Flugbahn eines Balls.
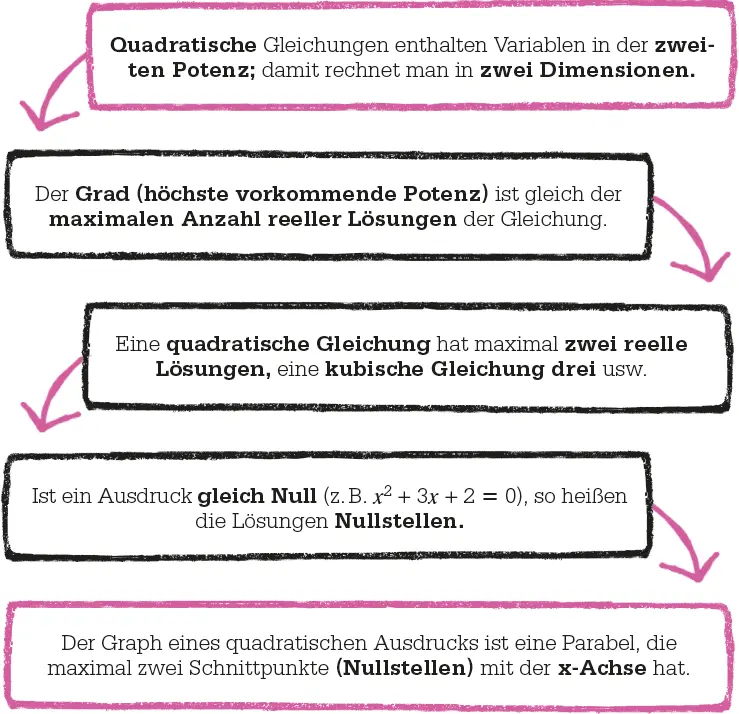
Die Geschichte der quadratischen Gleichungen erstreckt sich über die ganze Welt. Sie kamen vermutlich erstmals auf, um Fragen der Erbteilung von Land oder Probleme der Addition und Multiplikation zu lösen.
Eines der ältesten erhaltenen Beispiele einer quadratischen Gleichung findet sich in einem altägyptischen Text, dem Papyrus Berlin 6619 (um 1800 v. Chr.). Darin wird eine Aufgabe gestellt: Ein Quadrat der Fläche 100 Quadrat-Ellen hat die gleiche Fläche wie zwei kleinere Quadrate. Die Seitenlänge x des kleinsten Quadrats ist die Hälfte plus ein Viertel der Seitenlänge y des anderen kleinen Quadrats. In moderner Notation ergeben sich zwei Gleichungen die gleichzeitig erfüllt sein müssen: x 2+ y 2= 100 und x = (½ + ¼) · y = ¾ y . Sie lassen sich zu einer quadratischen Gleichung (¾ y ) 2+ y 2= 100 vereinfachen.
Um die Lösung zu finden, verwendeten die Ägypter ein Verfahren, das heute Regula-falsi -Methode (»Regel des Falschen«) heißt. Dazu wählt man für die Unbekannte einen »Ansatz«, eine beliebige »falsche« Zahl (meist eine, mit der leicht zu rechnen ist), und berechnet damit den Wert der Gleichung. Dann variiert man den Ansatz, um den richtigen Wert zu erhalten. In der Aufgabe des Berliner Papyrus ist der einfachste Ansatz 4 für die Seitenlänge y des größeren der kleinen Quadrate, weil man Viertel berechnen muss. Dann wäre die Seitenlänge x des kleineren Quadrats 3 (nämlich ¾ des größeren). Die Flächen der Quadrate wären dann 16 und 9, was zusammen 25 ergibt. Das ist nur ¼ des gewünschten Ergebnisses von 100. Man muss also die »falschen« Flächen vervierfachen, d. h. man muss die »falschen« Seitenlängen (4 und 3) verdoppeln und erhält so die richtigen Seitenlängen x = 6 und y = 8.

Der Berliner Papyrus ,1900 von dem deutschen Ägyptologen Hans Graf von Schack-Schackenburg veröffentlicht, enthält zwei mathematische Probleme, darunter eine quadratische Gleichung.
Weitere Belege für quadratische Gleichungen finden sich in babylonischen Tontafeln: Die Diagonale eines Quadrats wurde bis auf fünf Nachkommastellen genau angegeben. Die Tafel Yale Babylonian Collection (YBC) 7289 (um 1800–1600 v. Chr.) zeigt eine Lösungsmethode für die quadratische Gleichung x 2= 2, bei der man Rechtecke zeichnet und zu Quadraten verkleinert. Im 7. Jahrhundert n. Chr. beschrieb der indische Mathematiker Brahmagupta eine Lösung für quadratische Gleichungen der Form ax 2+ bx = c . Er verwendete noch keine Symbole, doch was er in Worten beschrieb, entsprach dieser Notation.
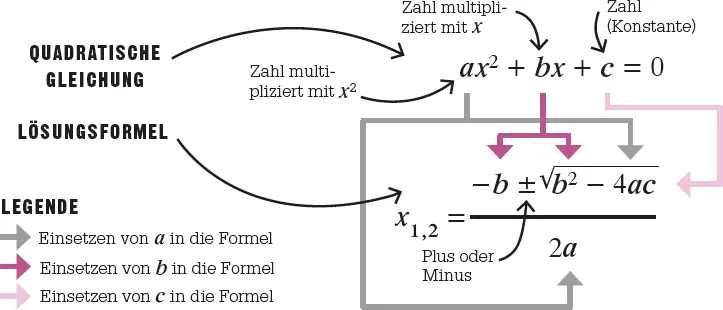
Für quadratische Gleichungengibt es eine Lösungsformel (»Mitternachtsformel«, weil Schüler sie wissen sollten, wenn man sie um Mitternacht weckt). Um sie zu benutzen schreibt man quadratische Gleichungen als Zahl a , multipliziert mit x 2, plus einer Zahl b mal x plus einer Zahl c gleich Null auf. Die Lösungen sind grafisch leicht zu sehen: die Punkte, an denen die Kurve die x -Achse schneidet. Die Abbildung unten zeigt, wie man a, b und c in die Formel einsetzt, um die zwei Lösungen x 1und x 2zu berechnen.
Im 8. Jahrhundert benutzte der persische Mathematiker al-Chwarizmi eine geometrische Lösungsmethode für quadratische Gleichungen, die heute quadratische Ergänzung heißt. Bis ins 10. Jahrhundert waren geometrische Methoden üblich, weil es eher um praktische Fragen, etwa der Landvermessung, als um abstrakte algebraische Herausforderungen ging.
Indische, persische und arabische Gelehrte hatten bis dahin nur positive Zahlen benutzt. Für die Gleichung x 2+ 10 x = 39 etwa gaben sie die Lösung 3 an. Doch das ist nur eine der beiden korrekten Lösungen des Problems, –13 ist die andere: Für x = –13 ist x 2= 169 und 10 x = –130. Das Addieren einer negativen Zahl entspricht dem Subtrahieren der Positiven: 169 + (– 130) = 169 – 130 = 39.
Im 10. Jahrhundert verwendete der ägyptische Gelehrte Abu Kamil Schudscha ibn Aslam negative Zahlen und irrationale Zahlen (etwa die Quadratwurzel von 2) sowohl als Lösungen als auch als Koeffizienten (Zahlenfaktoren vor der Unbekannten in der Gleichung). Im 16. Jahrhundert hatten die meisten Mathematiker negative Lösungen und irrationale Wurzeln (die sich nicht als genaue Dezimalzahl schreiben lassen) akzeptiert. Man hatte auch angefangen, Ausdrücke mit Symbolen statt in Worten zu schreiben. Das Plusminuszeichen (±) kam in Lösungen quadratischer Gleichungen auf. So ist die Lösung von x 2= 2 nicht nur x = 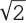 , sondern x 1,2= ±
, sondern x 1,2= ± 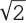 , d. h. die Wurzel kann positiv oder negativ sein, denn die Multiplikation zweier negativer Zahlen ist auch positiv: (–
, d. h. die Wurzel kann positiv oder negativ sein, denn die Multiplikation zweier negativer Zahlen ist auch positiv: (– 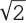 ) · (–
) · (– 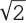 ) = 2.
) = 2.
Читать дальше






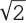 , sondern x 1,2= ±
, sondern x 1,2= ± 










