1545 veröffentlichte der Italiener Gerolamo Cardano Artis Magna, sive de Regulis Algebraicis (»Große Kunst«, oder »Algebraische Regeln«), in dem folgendes Problem vorkommt: »Welche zwei Zahlen haben die Summe 10 und das Produkt 40?« Das Problem führt auf eine quadratische Gleichung und zu den Lösungen 5 ± 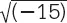 . Keine der damals bekannten Zahlen ergab eine negative Zahl, wenn man sie mit sich selbst multiplizierte, aber Cardano schlug vor, dennoch mit der Quadratwurzel der negativen Zahl zu rechnen, um die beiden Lösungen zu finden. Zahlen wie
. Keine der damals bekannten Zahlen ergab eine negative Zahl, wenn man sie mit sich selbst multiplizierte, aber Cardano schlug vor, dennoch mit der Quadratwurzel der negativen Zahl zu rechnen, um die beiden Lösungen zu finden. Zahlen wie 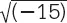 nennt man heute imaginäre Zahlen.
nennt man heute imaginäre Zahlen.
Heute schreibt man quadratische Gleichungen als ax 2+ bx + c = 0. Darin sind a, b und c bekannte Zahlen (Koeffizienten) und x die unbekannte Zahl. Gleichungen enthalten Variablen (Symbole für Unbekannte), Koeffizienten und Konstanten (feste Zahlen) sowie Operatoren (Rechenzeichen wie Plus- oder Gleichheitszeichen). Terme nennt man Ausdrücke, die von Operatoren getrennt werden. Das können Zahlen, Variablen oder Kombinationen beider sein. Die quadratische Gleichung in moderner Notation hat vier Terme: ax 2, bx , c und 0.
»Politik ist für die Gegenwart, aber eine Gleichung ist etwas für die Ewigkeit. «
Albert Einstein
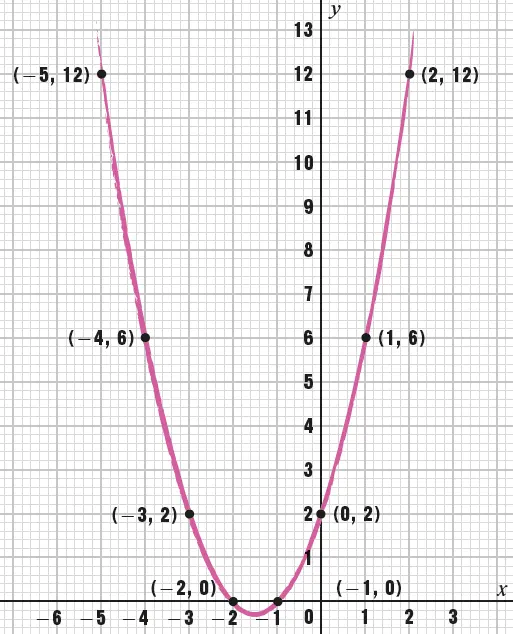
Der Grapheiner quadratischen Funktion y = ax 2+ bx + c ist eine etwa u-förmige Kurve, die man Parabel nennt. Diese Abbildung zeigt den Graph der Funktion für a = 1, b = 3 und c = 2, also y = x 2+ 3 x + 2. Ganzzahlige Werte sind als schwarze Punkte hervorgehoben. Die Nullstellen sind diejenigen x , für die y = 0 gilt, in denen also die Kurve die x -Achse schneidet. Hier: x = –2 und x = –1.
Eine Funktion stellt die Beziehung zwischen Variablen (oft x, y ) dar. Der Graph einer quadratischen Funktion y = ax 2+ bx + c beschreibt eine Kurve, die man Parabel nennt (siehe oben). Lösungen von ax 2+ bx + c = 0 heißen Nullstellen. Wenn reelle (nicht imaginäre) Nullstellen existieren, dann schneidet die Kurve die x -Achse. Nicht alle Parabeln schneiden die x -Achse zweimal. Berührt die Parabel die x -Achse nur in einem Punkt, sind die zwei Lösungen gleich (doppelte Nullstelle). Der einfachste Fall ist y = x 2. Schneidet die Parabel die x -Achse gar nicht, gibt es keine reellen Lösungen.
Parabeln haben wichtige Anwendungen. So haben Satellitenschalen eine parabolische Form, weil alle Signale aus einer Richtung (vom Satelliten) dann so reflektiert werden, dass sie an einem einzigen Punkt auftreffen: dem Empfänger. 
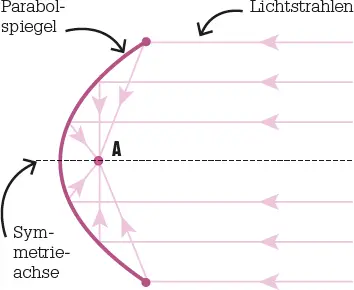
Ein Parabolspiegelist ein Paraboloid (ein Körper, der durch die Rotation einer Parabel entsteht). Lichtstrahlen parallel zur Symmetrieachse werden im Brennpunkt A gesammelt.
Anwendungen
Zwar dienten quadratische Gleichungen ursprünglich zur Lösung geometrischer Probleme, doch heute sind sie in vielen Bereichen der Mathematik, Wissenschaft und Technik wichtig. So werden etwa Flugbahnen damit modelliert: Wirft man ein Objekt in die Höhe, fällt es durch die Schwerkraft wieder nach unten. Die Höhe in Abhängigkeit der Zeit kann durch eine quadratische Funktion angegeben werden. Generell beschreiben quadratische Gleichungen oft die Beziehung zwischen Zeit, Strecke und Geschwindigkeit und sie sind bei Berechnungen von paraboloiden Objekten wie Linsen ein wichtiges Hilfsmittel. Auch ökonomische Vorhersagen nutzen sie. Unternehmen stellen eine quadratische Gleichung, (Gewinnfunktion) auf, um den optimalen Preis zu berechnen, der den Gewinn maximiert.

Quadratische Gleichungenwerden beispielsweise gebraucht, um die Flugbahnen von Geschossen zu berechnen – wie bei dieser Boden-Luft-Rakete MIM-104 Patriot, einer häufigen Rakete der US-Armee.

GENAUES RECHNEN: KENNTNIS ALLER DINGE DIESER WELT
DER PAPYRUS RHIND
IM KONTEXT
SCHLÜSSELZIVILISATION
Altes Ägypten(um 1650 v. Chr.)
SCHWERPUNKT
Arithmetik
FRÜHER
um 2480 v. Chr.Steinritzungen halten die Nilfluten fest, gemessen in Meh (Königsellen, etwa 52,4 cm) und Schesep (Handbreiten, 7,5 cm).
um 1850 v. Chr.Der Papyrus Moskau 4676 enthält Lösungen für 25 mathematische Probleme, darunter die Berechnung der Oberfläche einer Halbkugel und des Volumens einer Pyramide.
SPÄTER
um 1800 v. Chr.Der Berliner Papyrus zeigt die Verwendung einer quadratische Gleichung.
6. Jh. v. Chr.Der Grieche Thales von Milet reist nach Ägypten und studiert dort die mathematischen Theorien.
Der Papyrus Rhind im Britischen Museum in London gibt einen faszinierenden Einblick in die Mathematik des alten Ägypten. Er wurde nach dem schottischen Anwalt und Ägyptologen Alexander Henry Rhind benannt, der ihn 1858 in Ägypten erwarb. Der Text wurde von dem Schreiber Ahmose vor über 3500 Jahren von anderen Dokumenten kopiert. Der Papyrus ist 32 cm mal 200 cm groß und enthält 84 Probleme der Arithmetik, Algebra, Geometrie und der Vermessung. Dieser Papyrus sowie der etwas ältere Papyrus Moskau 4676 und einige weitere Fragmente dokumentieren Techniken zur Berechnung von Flächen, Verhältnissen und Volumen.

Das Auge des Gottes Horuswar ein Symbol der Macht und des Schutzes. Mit Teilen des Symbols repräsentierte man auch Bruchzahlen, deren Nenner Potenzen von 2 sind, der Augapfel etwa für ¼ und die Augenbrauen für 1/ 8.
Das ägyptische Zahlensystem war das erste System mit der Basis 10, aber kein Stellenwertsystem. Es nutzte Striche für die Einerziffern und verschiedene Symbole für Potenzen von 10, andere Zahlen wurden aus diesen Symbolen zusammengesetzt. Bruchzahlen stellte man durch einen Punkt über der Zahl dar. Damit ließen sich aber nur Stammbrüche bilden – also Brüche der Form 1/ n, wobei n eine positive, ganze Zahl ist. Andere Brüche musste man als Summe von Stammbrüchen schreiben: 2/ 3etwa war in ägyptischer Notation ½ + 1/ 6(nicht 1/ 3+ 1/ 3, da man den gleichen Stammbruch nicht wiederholte).
Читать дальше

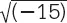 . Keine der damals bekannten Zahlen ergab eine negative Zahl, wenn man sie mit sich selbst multiplizierte, aber Cardano schlug vor, dennoch mit der Quadratwurzel der negativen Zahl zu rechnen, um die beiden Lösungen zu finden. Zahlen wie
. Keine der damals bekannten Zahlen ergab eine negative Zahl, wenn man sie mit sich selbst multiplizierte, aber Cardano schlug vor, dennoch mit der Quadratwurzel der negativen Zahl zu rechnen, um die beiden Lösungen zu finden. Zahlen wie 
















