John Farndon - Big Ideas. Das Mathematik-Buch

Der babylonische Sonnengott Shamashbelohnt auf dieser Tontafel von etwa 1000 v. Chr. neu ausgebildete Landvermesser mit einem Stab mit aufgewickeltem Seil als Messgerät.

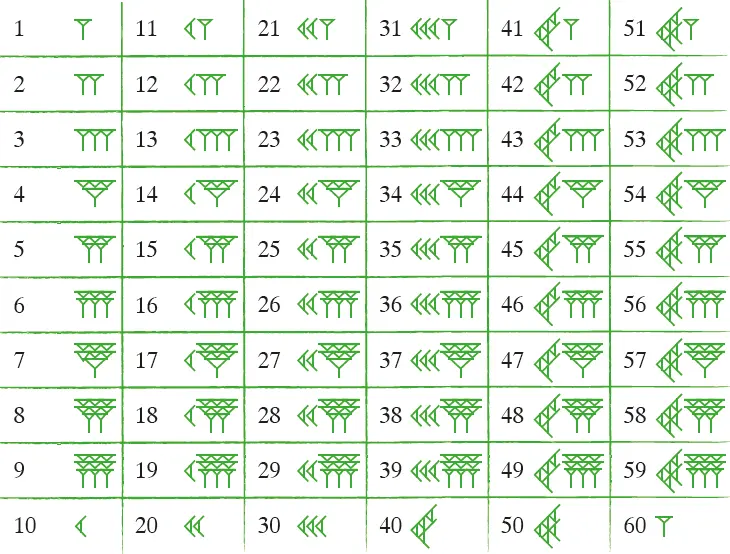
Das babylonische Zahlensystem zur Basis 60wiederholte zwei Symbole: das Einersymbol für die Zahlen 1 bis 9 und das Zehnersymbol für 10, 20, 30, 40 und 50.

Auf der anderen Seite der Erde, in Mittelamerika, entwickelten die Maya ein fortgeschrittenes Zahlensystem im 1. Jahrtausend v. Chr. – offenbar völlig eigenständig. Es war ein Vigesimalsystem (Zwanzigersystem), also ein System zur Basis 20, das wohl aus dem Zählen mit Fingern und Zehen entstand. Tatsächlich gab es Zwanzigersysteme auch in Europa, Afrika und Asien. So heißt 80 auf Französisch quatre-vingt (»vier-zwanzig«, 4 · 20). Walisisch und Irisch drücken ebenfalls einige Zahlen als Vielfache von 20 aus. Die Stiege und das englische Score sind Handelsmaße für 20 Stück. So gibt die englische King-James-Bibel (1611) in Psalm 90 die Lebenszeit von Menschen als threescore years and ten (3 · 20 + 10 = 70 Jahre) bis fourscore years (4 · 20 = 80 Jahre) an.

Ab etwa 500 v. Chr. bis zum 16. Jahrhundert, als man offiziell die indisch-arabischen Zahlen übernahm, verwendete man in China Stabzahlen. Es war das erste Zehnersystem: Durch Kombinationen senkrechter und waagrechter Stäbe konnte man Zehner, Hunderter, Tausender und höhere Potenzen von 10 darstellen, ähnlich wie in unserem heutigen Zahlensystem. So schrieb man 45 als vier horizontale Stäbe für 4 · 10 1(= 40) und fünf vertikale Stäbe für 5 · 1 (= 5). Dagegen ergaben vier vertikale, gefolgt von fünf weiteren vertikalen Stäben 405, nämlich 4 · 10 2+ 5 · 1. Fehlten horizontale Stäbe, so hatte die Zahl keine Zehnerstellen. Zum Rechnen nutzte man Zählstäbe auf einem Rechenbrett, wobei man positive und negative Zahlen durch schwarze bzw. rote Stäbe oder verschiedene Stabquerschnitte (drei- bzw. viereckig) unterschied. Stabzahlen werden in China heute noch gelegentlich verwendet, so wie man im Westen manchmal römische Zahlen nutzt.

Das chinesische Stellenwertsystem spiegelt sich auch im Abakus (Suanpan) wider. Er datiert auf vor 200 v. Chr. und ist damit eine der ältesten Rechenhilfen. Auch in Rom gab es ein ähnliches Gerät. Das chinesische Suanpan , das heute noch verwendet wird, hat einen horizontalen Mittelbalken und eine variable Zahl vertikaler Drähte für die Einer, Zehner, Hunderter usw. Auf jedem Draht sitzen über dem Balken zwei Kugeln, die jeweils fünf bedeuten, und darunter fünf Kugeln mit jeweils dem Wert eins.

In Japan wurde das Suanpan im 14. Jahrhundert übernommen und zu einer neuen Form, dem Soroban , weiterentwickelt, mit einer Kugel mit Wert fünf über dem Balken und vier Kugeln mit Wert eins darunter. Er wird in Japan noch heute verwendet. Es gibt sogar Wettbewerbe, Soroban -Rechnungen im Geist auszuführen (genannt Anzan) .

»Die babylonische und assyrische Zivilisation sind untergegangen … doch die babylonische Mathematik ist immer noch interessant, und die babylonische Skala von 60 wird in der Astronomie immer noch verwendet. «

G. H. HardyBritischer Mathematiker A Mathematician’s Apology , 1940

»Dass wir in Zehnern statt irgendeiner anderen Zahl arbeiten, ist alleine eine Folge unserer Anatomie. Wir verwenden unsere zehn Finger zum Zählen. «

Marcus du SautoyBritischer Mathematiker When numbers were dotty in: Telegraph , 29. Sept. 2011

Das indisch-arabische Dezimalsystem, das heute auf der ganzen Welt verwendet wird, hat seinen Ursprung in Indien. Im 1. bis 4. Jahrhundert n. Chr. wurde dieses Stellenwertsystem mit neun Zahlsymbolen und der Null entwickelt. Man kann damit jede Zahl effizient schreiben. Das System wurde im 9. Jahrhundert von islamischen Mathematikern übernommen und verbessert. Sie führten ein Dezimaltrennzeichen (entsprechend unserem Dezimalkomma) ein, um Dezimalbrüche auszudrücken.

Drei Jahrhunderte später machte Leonardo von Pisa (Fibonacci) die indisch-arabischen Zahlen im Liber Abbaci (»Buch vom Rechnen«, 1202) in Europa bekannt. Doch die Debatte, ob diese Zahlen traditionelle römische Zahlen und Rechenmethoden ersetzen sollten, dauerte mehrere hundert Jahre an. Schließlich setzte sich das neue System durch und ermöglichte viele moderne Fortschritte.

Mit dem Aufkommen von Computern wurden andere Zahlenbasen wichtig, vor allem die Basis 2: das Binärsystem. Anders als das Dezimalsystem mit zehn Zahlzeichen hat das Binärsystem nur zwei: 0 und 1. Es ist ein Stellenwertsystem, bei dem jede Stelle mit 2 statt mit 10 multipliziert wird, ausgedrückt als 2 0, 2 1, 2 2, 2 3usw. Die Binärzahl 111 bedeutet 1 · 2 2+ 1 · 2 1+ 1 · 2 0, also im Dezimalsystem 4 + 2 + 1 = 7.

Ebisu, der japanische Gottder Fischer und einer der sieben Glücksgötter, berechnet seinen Profit mit einem Soroban in Der Traum des Roten Schnappers von Utagawa Toyohiro.

Das Binärsystem folgt den Prinzipien aller modernen Zahlensysteme jeder Basis. Das Stellenwertsystem – ein babylonisches Erbe – ist immer noch eine mächtige, verständliche und effiziente Art, große Zahlen darzustellen.

Keilschrift

Im späten 19. Jahrhundert entzifferte man die keilförmigen Zeichen auf babylonischen Tontafeln, die im und um den Irak gefunden wurden. Die Markierungen, die Buchstaben und Ziffern eines komplexen Zahlensystems darstellten, wurden mit beiden Enden eines Schreibgriffels in weichen Ton gedrückt. Wie später in Ägypten verwalteten Schreiber in Babylonien die Gesellschaft, daher stammen wohl viele der Tontafeln aus Schulen, in denen sie ausgebildet wurden.

Heute wissen wir eine Menge über die babylonische Mathematik, die sich über Multiplikation, Division, Geometrie, Bruchrechnung, Quadrat- und Kubikwurzeln, Gleichungen und mehr erstreckte, denn Tontafeln haben sich (anders als ägyptische Papyri) gut erhalten. Mehrere tausend, vor allem von 1800–1600 v. Chr., befinden sich heute in Museen der ganzen Welt.

Keilschrift,benannt nach dem keilförmigen Aussehen der Zeichenelemente, wurde auf feuchtem Ton geschrieben, in Stein gemeißelt oder Metall graviert.

Zahlensystem der Maya

Die Maya, deren Kultur in Mittelamerika um 2000 v. Chr. aufkam, verwendeten ab etwa 1000 v. Chr. ein Zwanzigersystem (Vigesimalsystem) für astronomische und kalendarische Berechnungen. Wie bei den Babyloniern hatte der Kalender 360 Tage plus Festtage, was im Mittel ein Sonnenjahr von 365,24 Tagen ergab. Er half insbesondere bei der Landwirtschaft.