John Farndon - Big Ideas. Das Mathematik-Buch

Ab dem 6. Jahrhundert v. Chr. nahm der Einfluss Griechenlands im östlichen Mittelmeerraum rapide zu. Griechische Gelehrte übernahmen mathematische Konzepte aus Babylonien und Ägypten. Die Griechen benutzten ein Stellenwertsystem zur Basis 10 (also zehn Zahlzeichen), abgeleitet vom ägyptischen System. Vor allem die Geometrie schwang mit der griechischen Kultur mit, die Formen und Symmetrien schätzte. Die Mathematik wurde zu einer Basis des Denkens und zeigte sich in der Kunst, Architektur und sogar der Philosophie. Die fast mystischen Eigenschaften der Geometrie und der Zahlen inspirierten Pythagoras und seine Anhänger zur Gründung einer fast kultartigen Gemeinde. Sie betrachteten mathematische Prinzipien, die sie als Fundament des Universums und aller Dinge ansahen.

Jahrhunderte vor Pythagoras hatten Ägypter Dreiecke mit Seiten von 3, 4 und 5 Längeneinheiten benutzt, um beim Bau rechte Winkel zu konstruieren. Diese Faustregel hatten sie durch zufällige Beobachtungen entdeckt. Doch die Pythagoreer fanden einen strikten Beweis für einen allgemeinen Satz über die Seitenverhältnisse rechtwinkliger Dreiecke. Die Grundidee, allgemeine Sätze strikt zu beweisen, gilt als einer der wichtigsten Beiträge der Griechen zur Mathematik.

Platons Akademie in Athen war der Philosophie und der Mathematik gewidmet, und Platon selbst beschrieb die fünf platonischen Körper (Tetraeder, Würfel, Oktaeder, Dodekaeder und Ikosaeder). Man wandte Logik auf die Grundlagen der Mathematik an. Insbesondere deckte Zenon von Elea logische Probleme der Unendlichkeit und des Wandels auf. Die Griechen erforschten auch die seltsamen Merkmale irrationaler Zahlen. Platons Schüler Aristoteles erkannte durch die methodische Analyse logischer Formen den Unterschied zwischen Induktion (von Beobachtungen allgemeine Regeln ableiten) und Deduktion (aus etablierten Annahmen bzw. Axiomen durch logische Schritte folgern).

Darauf aufbauend erklärte Euklid das Prinzip mathematischer Beweise aus axiomatischen Wahrheiten in seinem Werk Elemente . Es bildete zwei Jahrtausende lang die Grundlage der Mathematik. Mit ähnlicher Sorgsamkeit verwendete Diophantos von Alexandria Buchstabensymbole für unbekannte Zahlen in Gleichungen: ein wichtiger Schritt zur symbolischen Notation in der Algebra.

Der griechische Einfluss wurde schließlich vom Aufstieg Roms überschattet. Für die Römer war die Mathematik eher ein praktisches Werkzeug als ein würdiges Studienthema. Etwa zur gleichen Zeit entstanden in Indien und China jeweils eigene Zahlensysteme. Insbesondere in China erblühte die Mathematik zwischen dem 2. und 5. Jahrhundert n. Chr. vor allem dank Liu Hui, der die klassischen Texte der chinesischen Mathematik überarbeitete und erweiterte.

IM KONTEXT

SCHLÜSSELZIVILISATION

Babylonier

TEILGEBIET

Arithmetik

FRÜHER

vor 40 000 JahrenMenschen der Steinzeit in Europa und Afrika kerben Strichlisten auf Holz und Knochen.

3500–3200 v. Chr.Die Sumerer haben Rechensysteme zur Landvermessung und für astronomische Beobachtungen.

3200–3000 v. Chr.Die Babylonier verwenden kleine Tonkegel als Symbol für 1, große Kegel für 60 und Tonkugeln für 10 als Schritt zum Stellenwertsystem mit der Basis 60.

SPÄTER

2. Jh. n. Chr.Die Chinesen entwickeln den Abakus für ihr Zehnersystem.

7. Jh.In Indien führt Brahmagupta die Null als eigenständige Zahl, nicht nur als Platzhalter, ein.

»Es ist uns gegeben zu rechnen, zu wiegen, zu messen, zu beobachten; das ist Naturphilosophie. «

VoltaireFranzösischer Philosoph

Die früheste Kultur, von der wir ein fortgeschrittenes Zahlensystem kennen, ist die sumerische Hochkultur in Mesopotamien, dem Zweistromland zwischen den Flüssen Tigris und Euphrat im heutigen Irak. Schon ab dem 4. Jahrtausend v. Chr. zeigen sumerische Tontafeln Symbole für verschiedene Mengenangaben. Die Sumerer, und später die Babylonier, brauchten effiziente mathematische Hilfsmittel für die Verwaltung ihrer komplexen Staaten.

Was die Babylonier von anderen Völkern – etwa den Ägyptern – unterschied, war das Stellenwertsystem. Bei diesen Zahlensystemen wird der Wert einer Ziffer sowohl vom Symbol als auch von seiner Stelle (der Position relativ zu anderen Ziffern) bestimmt. Im heutigen Zehnersystem bestimmt die Stelle eines Zahlzeichens, ob es ein Vielfaches von eins, zehn, hundert usw. darstellt. Berechnungen sind in Stellenwertsystemen effizienter, weil man mit einer kleinen Anzahl von Zeichen eine enorme Menge an Zahlen darstellen kann. Dagegen hatten die Ägypter verschiedene Zeichen für Einer, Zehner, Hunderter, Tausender usw. und kein Stellenwertsystem. Große Zahlen erforderten 50 oder mehr Hieroglyphen.

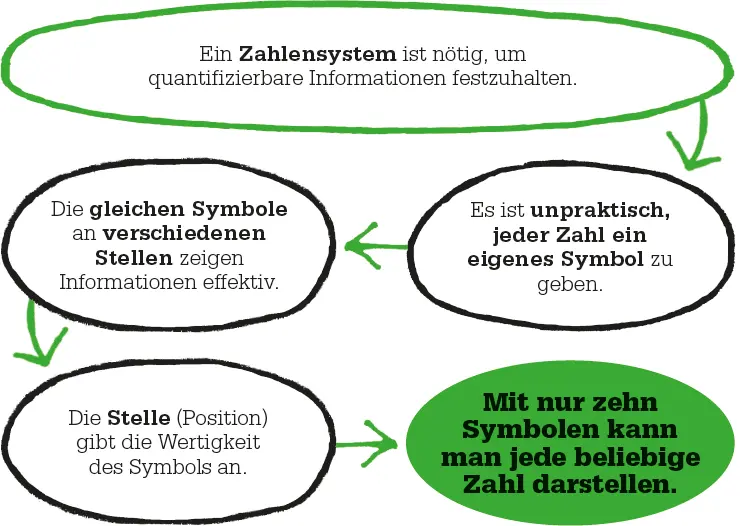
Das indisch-arabische System, das wir heute verwenden, ist ein Zehner- bzw. Dezimalsystem. Seine Basis ist zehn, d. h. man braucht nur zehn Zahlzeichen: die zehn Ziffern 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Die Stelle einer Ziffer zeigt die Wertigkeit an, wobei die niedrigste Stelle rechts steht. Die Zahl 22 im Dezimalsystem bedeutet (2 · 10 1) + 2. Der Wert der linken 2 ist zehnmal so groß wie der Wert der rechten 2. Weitere Stellen links davon bedeuten Hunderter, Tausender und höhere Potenzen von zehn. Im gleichen System kann man auch Bruchteile darstellen: Ziffern rechts der ganzen Zahl nach einem Dezimaltrennzeichen (im Deutschen und in vielen anderen Sprachen ein Komma, im Englischen ein Punkt) haben jeweils ein Zehntel der Wertigkeit der vorangehenden Stelle.

Die Babylonier arbeiteten mit dem System zur Basis 60, dem Sexagesimalsystem (auch Hexagesimal- oder Sechzigersystem), das sie wohl von den Sumerern übernommen hatten. Es wird heute noch für Zeiten, Winkelgrade (360 ° = 6 · 60) und geografische Koordinaten eingesetzt. Warum sie 60 als Basis wählten, ist immer noch nicht gesichert. Ein Grund könnte sein, dass man 60 durch sehr viele Zahlen teilen kann: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20 und 30. Zudem basierte der Kalender auf dem Sonnenjahr (365,24 Tage) und ihr Jahr hatte 360 (= 6 · 60) Tage mit zusätzlichen Festtagen.

Im babylonischen Sexagesimalsystem wurde ein Symbol (bis zu neunmal wiederholt) für die Zahlen 1 bis 9 verwendet. Für 10 gab es ein anderes Symbol, das links neben dem Einersymbol stand und bis zu fünfmal wiederholt wurde, um Zahlen bis 59 zu bilden. Für 60 (also 1 · 60) wurde wieder das Einersymbol verwendet, aber weiter links platziert als zur Darstellung der Eins. Weil es ein Stellenwertsystem zur Basis 60 war, repräsentierten zwei Einersymbole nebeneinander 1 · 60 + 1, also 61, und drei Symbole 1 · 60 2+ 1 · 60 + 1, also 3661.

Das Sexagesimalsystem hatte offensichtliche Nachteile. Es benötigt mehr Zahlzeichen als ein Zehnersystem. Zudem gab es jahrhundertelang keine Platzhalter und kein Trennzeichen, das den ganzzahligen Anteil vom Bruchteil einer Zahl trennt. Um 300 v. Chr. aber markierten die Babylonier fehlende Ziffern durch zwei Keile, ähnlich wie wir heute die Null als Platzhalter verwenden. Dies war wohl die früheste Verwendung der Null.