John Farndon - Big Ideas. Das Mathematik-Buch

Magische Quadrate waren zu allen Zeiten eine anhaltende Quelle der Faszination. Im 15. Jahrhundert sammelte der italienische Mathematiker Luca Pacioli, Autor von De Viribus Quantitatis (»Über die Macht der Zahlen«), magische Quadrate. Im 18. Jahrhundert erfand Leonhard Euler in der Schweiz eine verwandte Form, die lateinischen Quadrate. Sie enthalten Symbole (Buchstaben, Zahlen oder anderes), die in jeder Zeile und Spalte nur jeweils einmal auftreten dürfen.

Eine Variante lateinischer Quadrate ist heute ein beliebtes Rätsel: Sudoku. Erstmals in den 1970ern in den USA als Number Place veröffentlicht, wurden sie in den 1980ern in Japan populär. Das japanische Wort bedeutet »Ziffern kommen nur einmal vor«. Ein Sudoku ist ein lateinisches Quadrat neunter Ordnung (also 9×9) mit der Zusatzbedingung, dass auch jeder Teilbereich alle neun Zahlen enthalten muss.

»Das magisch magischste aller magischen Quadrate, das je ein Magier gemacht hat. «

Benjamin Franklinüber ein von ihm entdecktes magisches Quadrat Life of Benjamin Franklin, Written by Himself , 1887

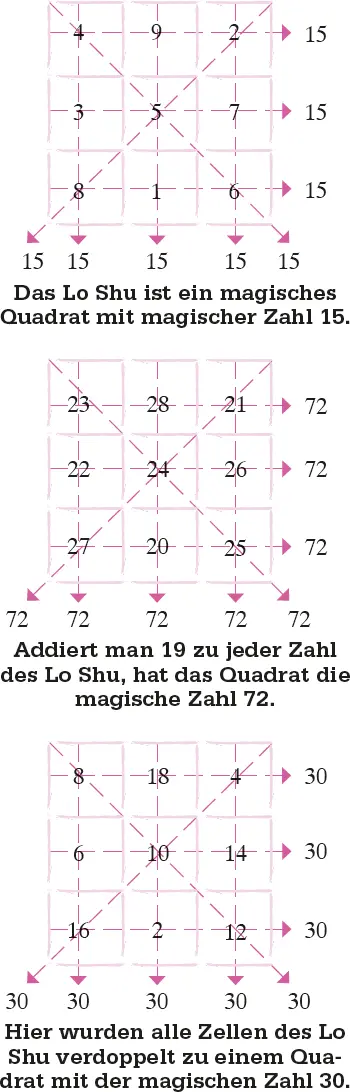
Addiert man bei einem magischen Quadratzu jeder Zahl den gleichen konstanten Wert, so entsteht wieder ein magisches Quadrat. Ebenso kann man jede Zahl mit einer Konstanten multiplizieren und das Ergebnis ist magisch.

IM KONTEXT

SCHLÜSSELFIGUR

Pythagoras(um 570–495 v. Chr.)

TEILGEBIET

Angewandte Geometrie

FRÜHER

um 1800 v. Chr.Die Tontafel Plimpton 322 aus Babylon enthält Spalten von Keilschriftzahlen, die mit pythagoreischen Tripeln verwandt sind.

6. Jh. v. Chr.Der Grieche Thales von Milet beschreibt eine nichtmythische Entstehung des Universums; er ist Vorreiter der Idee, dass die Natur rational verstehbar ist.

SPÄTER

um 380 v. Chr.Im zehnten Buch von Politeia unterstützt Platon den Glauben von Pythagoras an die Seelenwanderung.

um 300 v. Chr.Euklid findet eine Formel zur Bildung primitiver pythagoreischer Tripel.

Pythagoras, der griechische Philosoph aus dem 6. Jahrhundert v. Chr., dürfte wohl der berühmteste Mathematiker der Antike sein. Auch wenn unklar ist, ob er alle Leistungen in der Mathematik, Wissenschaft, Astronomie, Musik und Medizin, die ihm zugeschrieben werden, selbst erbracht hat, besteht kein Zweifel daran, dass er eine exklusive Gemeinschaft gründete, die für die Mathematik und die Philosophie lebte und die Zahlen als die heiligen Bausteine des Universums sah.

Die Pythagoreer waren Meister der Geometrie und wussten, dass die Innenwinkelsumme eines Dreiecks (180 °) gleich der Summe von zwei rechten Winkeln (90 ° + 90 °) ist. Euklid nannte dies später das Dreieckspostulat. Die Anhänger von Pythagoras kannten auch mehrere der konvexen regulären Polyeder. Diese dreidimensionalen Körper mit größtmöglicher Symmetrie nannte man später platonische Körper.

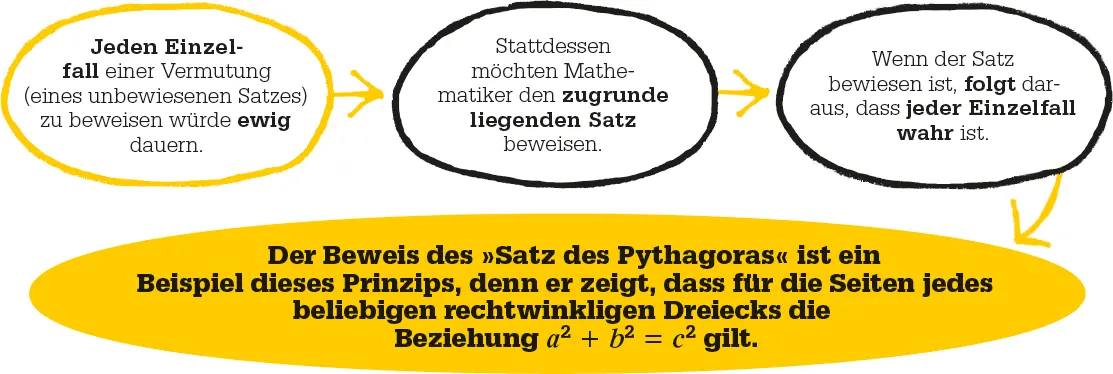
Pythagoras selbst ist vor allem für eine Gleichung bekannt: Sie beschreibt die Beziehung der Seitenlängen rechtwinkliger Dreiecke; der »Satz von Pythagoras«. In moderner Notation: a 2+ b 2= c 2, wobei c die längste Seite (Hypotenuse) ist und a, b die beiden anderen, kürzeren Seiten (Katheten) sind, die den rechten Winkel bilden.

Thales von Milet,einer der sieben Weisen von Griechenland, inspirierte vielleicht Pythagoras mit geometrischen und wissenschaftlichen Ideen. Vielleicht trafen sie sich in Ägypten.

Diese Zeichnungenzeigen, warum der Satz von Pythagoras ( a 2+ b 2= c 2) wahr ist. In dem großen Quadrat liegen vier rechtwinklige Dreiecke gleicher Größe (mit den Seitenlängen a, b und c ) so, dass in der Mitte ein großes Quadrat durch die Hypotenusen (den Seiten c ) der Dreiecke gebildet wird.

So hat etwa ein rechtwinkliges Dreieck mit den kurzen Seiten 3 cm und 4 cm eine Hypotenuse der Länge 5 cm, denn 3 2+ 4 2= 5 2(also 9 + 16 = 25). Tripel (Dreiertupel) von drei natürlichen Zahlen, die diese Gleichung erfüllen, nennt man pythagoreische Tripel. Multipliziert man das pythagoreische Tripel (3, 4, 5) mit 2, erhält man ein weiteres pythagoreisches Tripel: (6, 8, 10); es löst ebenfalls die Gleichung: 36 + 64 = 100. Das Tripel (3, 4, 5) nennt man »primitiv«, weil die drei Zahlen keinen gemeinsamen Teiler (außer 1) haben. Dagegen ist (6, 8, 10) nicht primitiv, denn die Zahlen haben den gemeinsamen Teiler 2.

Es gibt Hinweise, dass den Babyloniern und Chinesen die mathematische Beziehung zwischen den Seiten eines rechtwinkligen Dreiecks schon Jahrhunderte vor der Geburt von Pythagoras bewusst war. Doch Pythagoras dürfte als Erster den allgemeinen Beweis für die Formel erbracht und damit gezeigt haben, dass sie für alle rechtwinkligen Dreiecke gilt. Daher trägt der Satz heute seinen Namen.

Pythagoras reiste viel. Das Wissen, das er in anderen Ländern aufnahm, musste ihn zweifellos inspiriert haben. Er stammte aus Samos, unweit von Milet in Westanatolien (heutige Türkei). Vermutlich studierte er an der Schule des Thales von Milet unter dem Philosophen Anaximander. Mit 20 Jahren brach er für viele Jahre ins Ausland auf. Er besuchte wohl Phönizien, Persien, Babylon, Ägypten und könnte sogar Indien erreicht haben. Die Ägypter wussten, dass ein Dreieck mit den Seitenlängen 3, 4 und 5 (das erste pythagoreische Tripel) stets einen rechten Winkel hat. Baumeister verwendeten Schnüre mit diesen Längen, um präzise rechte Winkel zu konstruieren. Die Beobachtung dieser Praxis könnte Pythagoras dazu angeregt haben, den zugrunde liegenden mathematischen Satz zu beweisen. In Ägypten könnte er auch Thales von Milet getroffen haben, welcher Höhen von Pyramiden berechnete und das deduktive Schlussfolgern auf die Geometrie anwandte.

»Die Vernunft ist unsterblich, alles andere ist sterblich. «

Pythagoraszitiert in: Diogenes Laertios Vitae et Sententiae Philosophorum 3. Jh. n. Chr.

Nach 20 Jahren Reisen ließ sich Pythagoras schließlich in Kroton (heutiges Crotone) in Kalabrien (Süditalien) nieder, das eine große griechische Bevölkerung hatte. Dort gründete er die Pythagoreer – eine Gemeinschaft, in der er seine mathematischen und philosophischen Glaubensgrundsätze lehrte. Frauen waren in der Gemeinschaft willkommen und bildeten einen erheblichen Teil der etwa 600 Mitglieder. Mitglieder mussten ihren ganzen Besitz der Gemeinschaft übergeben und zudem schwören, die mathematischen Entdeckungen geheim zu halten. Unter Pythagoras erlangte die Gemeinschaft erheblichen politischen Einfluss.