John Farndon - Big Ideas. Das Mathematik-Buch

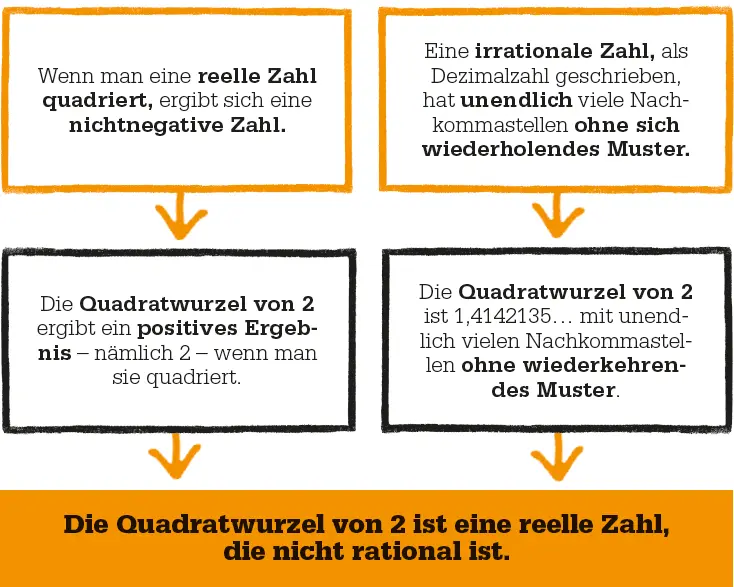
Das dezimale Stellenwertsystem der indisch-arabischen Zahlen ermöglicht weitere Charakterisierungen irrationaler Zahlen. Man kann zeigen, dass sie unendliche viele Nachkommastellen ohne wiederkehrendes Muster haben. So ist 0,1010010001… (unendlich fortgesetzt, jeweils mit einer weiteren 0 nach jeder 1) irrational. Pi ( π ), das Verhältnis des Umfangs zum Durchmesser eines Kreises, ist irrational, was 1761 von Johann Heinrich Lambert bewiesen wurde. Frühere Näherungswerte für π waren etwa 3 oder 22/ 7.

Zwischen zwei rationalen Zahlen liegen stets weitere rationale Zahlen, es gibt keine »Lücken«, denn der Mittelwert zweier rationalen Zahlen ist wieder rational, ebenso der Mittelwert vom vorigen und einer der beiden Ausgangszahlen usw. Zwischen beliebigen rationalen Zahlen liegen zudem stets irrationale Zahlen. Zum Beispiel kann man Ziffern in den unendlich wiederholten Nachkommastellen gedanklich ändern, um eine irrationale Zahl zwischen den beiden rationalen Zahlen 0,124124… und 0,125125… zu konstruieren. Dazu ändert man bei 0,124124… in immer größeren Abständen die 1 in eine 3.

Eine der großen Herausforderungen der modernen Mathematik war die Frage, ob es mehr rationale oder irrationale Zahlen gibt. Georg Cantor, der Begründer der Mengenlehre, konnte 1874 zeigen, dass die rationalen Zahlen abzählbar und die irrationalen Zahlen überabzählbar und damit »mächtiger« sind.

Hippasos

Die Details der jungen Jahre von Hippasos sind nur bruchstückhaft erhalten, er wurde um 500 v. Chr. in Metapont in Magna Graecia (heutiges Süditalien) geboren. Nach dem Philosophen Iamblichos, Autor einer Biografie von Pythagoras, war Hippasos der Gründer einer pythagoreischen Sekte, den Mathematici, deren Mitglieder fest daran glaubten, dass alle Zahlen rational seien.

Hippasos wird gewöhnlich die Entdeckung der irrationalen Zahlen zugeschrieben, was damals in der Sekte bestimmt als Ketzerei gegolten hätte. Nach einer Geschichte ertrank Hippasos, als ihn andere Pythagoreer voller Abscheu aus einem Boot über Bord warfen. Nach einer anderen Geschichte habe ein anderer Pythagoreer die irrationalen Zahlen entdeckt, aber Hippasos wurde bestraft, weil er Außenstehenden davon erzählt hatte. Hippasos starb etwa im 5. Jh. v. Chr., sein genaues Todesjahr ist unbekannt.

Hauptwerke

5. Jh. v. Chr. Mystischer Logos

IM KONTEXT

SCHLÜSSELFIGUR

Zenon von Elea(um 495–430 v. Chr)

TEILGEBIET

Logik

FRÜHER

Frühes 5. Jh. v. Chr.Der griechische Philosoph Parmenides gründet die eleatische Schule der Philosophie in Elea, einer griechischen Kolonie in Kampanien (Süditalien).

SPÄTER

350 v. Chr.Aristoteles schreibt das Werk Physik , in dem er Prinzipien der relativen Bewegung und Veränderung aufstellt, um Zenons Paradoxa zu lösen.

1914Der britische Philosoph Bertrand Russell, der Zenons Paradoxa als unmessbar subtil bezeichnet hat, stellt fest, dass Bewegung eine Funktion des Ortes in der Zeit ist.

Zenon von Elea gehörte zur eleatischen Philosophenschule, die im 5. Jahrhundert v. Chr. in Griechenland florierte. Anders als die Atomisten, die glaubten, das Universum könne in seine Bestandteile –Atome – zerlegt werden, glaubten Eleaten an die Unteilbarkeit aller Dinge.

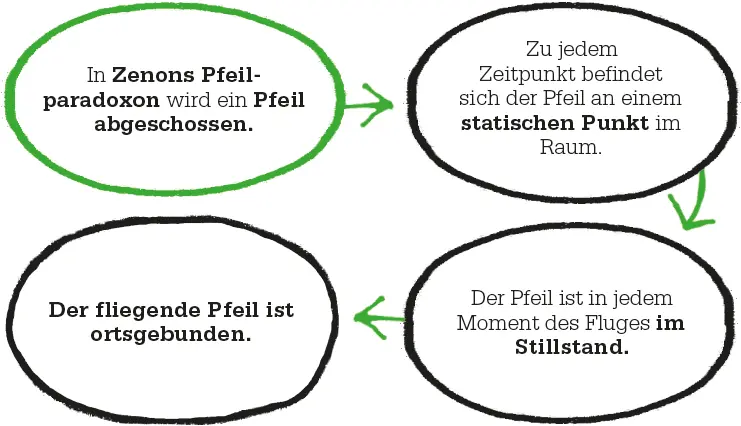
Zenon schrieb 40 Paradoxa, um die Absurdität des Atomismus zu zeigen. Vier davon – das Dichotomie- oder Teilungsparadoxon, das Paradoxon von Achilles und der Schildkröte, das Pfeilparadoxon und das Stadionparadoxon – behandeln die Bewegung. Das Dichotomieparadoxon soll die Absurdität der Ansicht zeigen, dass Bewegung teilbar ist: Wenn ein Körper eine bestimmte Distanz zurücklegen will, muss er erst den halben Wegpunkt vor dem Ende erreichen und davor den Viertelpunkt der Strecke usw. Da der Körper eine unendliche Anzahl von Punkten passieren muss, kann er nie ans Ziel kommen.

Im Paradoxon von Achilles und der Schildkröte laufen die beiden um die Wette. Achilles, der hundertmal so schnell ist, gibt dem Tier einen Vorsprung von 100 m. Beim Startsignal läuft Achilles 100 m bis zum Startpunkt der Schildkröte, doch die Schildkröte ist inzwischen 1 m gelaufen und hat nun 1 m Vorsprung. Achilles läuft einen weiteren Meter, doch in dieser Zeit läuft die Schildkröte um ein Hundertstelmeter weiter und liegt immer noch vorne. Dies geht unendlich weiter und Achilles sollte sie nie einholen.

Das Stadionparadoxon betrachtet drei Reihen von jeweils gleich vielen Menschen. Eine ist in Ruhe, während die anderen beiden in entgegengesetzter Richtung gleich schnell aneinander vorbei laufen. Demnach passiert eine Person in einer der Läuferreihen in einer festen Zeit zwei Personen in der anderen Läuferreihe, aber nur eine in der festen Reihe. Die paradoxe Schlussfolgerung daraus wäre, dass die Hälfte einer gegebenen Zeit gleich ihrem Doppelten ist.

Im Laufe der Jahrhunderte haben Mathematiker die Paradoxa aufgeklärt. Die Infinitesimalrechnung ermöglicht es, mit infinitesimalen (unendlich kleinen) Größen ohne Widersprüche zu rechnen.

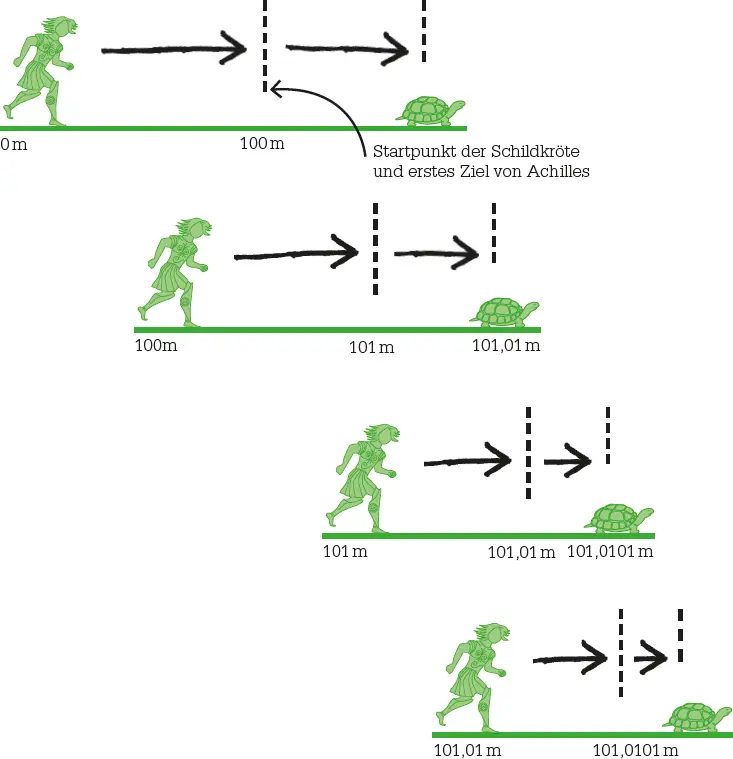
Das Paradoxonvon Achilles und der Schildkröte sagt aus, dass Achilles niemals die langsamere Schildkröte einholen kann, wenn er ihr einen Vorsprung gewährt. Achilles kommt zwar näher, aber die Schildkröte ist immer voraus.

Zenon von Elea

Zenon wurde um 495 v. Chr. in der griechischen Stadt Elea, dem heutigen Velia in Kampanien (Süditalien), geboren. Als Junge wurde er von dem Philosophen Parmenides adoptiert, der ihn »geliebt« haben soll. Zenon wurde in die eleatische Denkschule eingeweiht, die Parmenides gegründet hatte. Im Alter von etwa 40 Jahren reiste Zenon nach Athen, wo er Sokrates traf und die Sokratiker mit eleatischen Ideen bekanntmachte.

Zenon war für seine Paradoxien wohlbekannt. Sie halfen bei der Entwicklung strikter mathematischer Denkweisen. Aristoteles beschrieb ihn später als Erfinder der Dialektik, einer Argumentationsweise, bei der man von gegensätzlichen Standpunkten ausgeht. Zenon sammelte seine Argumente in einem Buch, das heute nicht mehr erhalten ist. Die Paradoxien sind aus Aristoteles’ Werk Physik bekannt, das neun auflistet.