John Farndon - Big Ideas. Das Mathematik-Buch

1854George Boole veröffentlicht The Laws of Thought , sein zweites Buch zur algebraischen Logik.

1884 Die Grundlagen der Arithmetik von Gottlob Frege untersucht die der Mathematik zugrundeliegenden logischen Prinzipien.

Im klassischen Griechenland unterschied man nicht klar zwischen Mathematik und Philosophie, sondern sie galten als verflochten. Ein wichtiges Prinzip der Philosophen war die Formulierung stichhaltiger Argumente, die auf logischen Folgerungen beruhten. Dies basierte auf der dialektischen Methode von Sokrates, Annahmen zu hinterfragen, um Widersprüchlichkeiten aufzudecken. Aristoteles fand dieses Modell jedoch nicht völlig zufriedenstellend und wollte die systematische Struktur logischer Argumente genauer ausarbeiten. Zunächst identifizierte er verschiedene mögliche Typen von Aussagen und wie man sie verknüpft, um logische Folgerungen zu erhalten. In Analytica Priora beschreibt er, dass es vier grundsätzliche Formen von Aussagen gibt: »Alle S sind P«, »Kein S ist P«, »Einige S sind P« und »Einige S sind nicht P«, wobei S ein Subjekt wie etwa »Frucht« ist und P ein Prädikat, eine Qualität oder ein Merkmal wie etwa »süß«. Schon aus zwei solcher Aussagen kann man ein logisches Argument konstruieren. Diese logische Form nennt man Syllogismus: Zwei Prämissen, die zu einer Schlussfolgerung führen. Aristoteles identifizierte die Struktur von Syllogismen, die logisch gültig sind, bei denen also die Schlussfolgerung tatsächlich aus den Prämissen folgt, und diejenigen, bei denen dies nicht der Fall ist. Damit schuf er eine Methode sowohl zur Konstruktion als auch zur Analyse logischer Argumente.

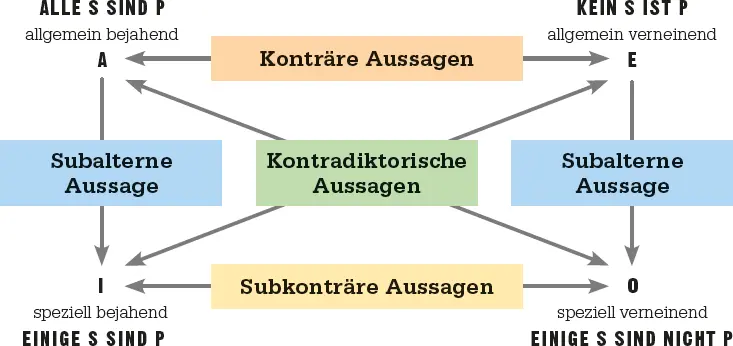
Im logischen Quadratist S ein Subjekt, z. B. »Frucht«, und P ein Prädikat, z. B. »süß«. A und O sind widersprüchlich, ebenso wie E und I: Wenn eines wahr ist, ist das andere falsch, und umgekehrt. A und E sind konträr: Beide können nicht wahr sein, aber beide können falsch sein. I und O sind subkonträr: Beide können wahr, aber nicht beide falsch sein. I folgt aus A, d. h. wenn A wahr ist, muss auch I wahr sein, doch wenn I falsch ist, ist auch A falsch. Das gleiche gilt für E und O.

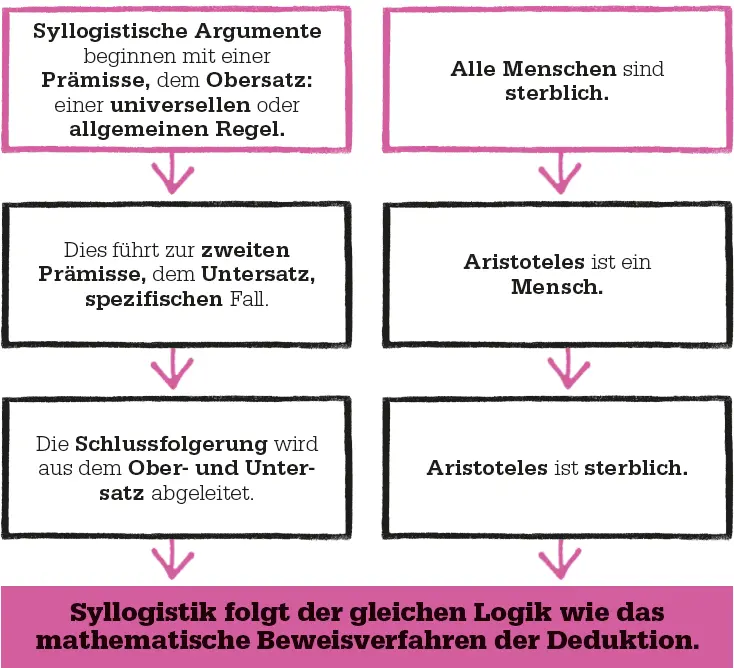
In der Diskussion gültiger Syllogismen ist die Beweismethode der Deduktion eingeschlossen. Sie geht von zwei Prämissen aus, dem Obersatz, einer allgemeinen Aussage wie »alle Menschen sind sterblich«, und dem Untersatz, einem spezifischen Fall wie »Aristoteles ist ein Mensch«, und schlussfolgert daraus. Hier: »Aristoteles ist sterblich«. Diese deduktive Argumentationsweise ist die Basis mathematischer Beweise.

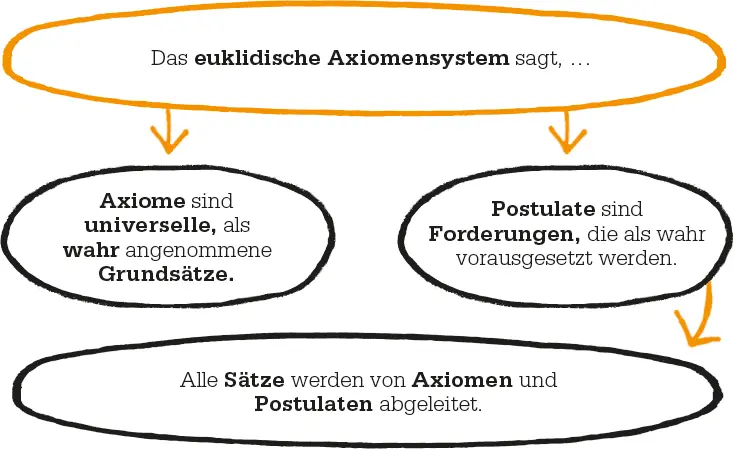
In Analytica Posteriora merkt Aristoteles an, dass selbst in einem gültigen Syllogismus die Schlussfolgerung nur wahr ist, wenn man die Prämissen als wahr akzeptiert, etwa offensichtliche Tatsachen oder Axiome. Damit etablierte er das Prinzip axiomatischer Wahrheiten als Basis für die logische Weiterentwicklung von Ideen – Vorlage für mathematische Theoreme seit Euklid.

Aristoteles

Der Sohn eines Arztes am makedonischen Hof wurde 384 v. Chr. in Stagira (Chalkidiki) geboren. Mit etwa 17 Jahren ging Aristoteles nach Athen, um an Platons Akademie zu studieren, wo er ein exzellenter Schüler war. Kurz nach Platons Tod musste er aufgrund antimakedonischer Stimmungen Athen verlassen. Er setzte seine Arbeit in Assos (heutige Türkei) fort. 343 v. Chr. rief ihn Philipp II. nach Makedonien zurück, um die Hofschule zu führen. Einer der Schüler war sein Sohn Alexander der Große.

335 v. Chr. kehrte Aristoteles nach Athen zurück und gründete das Lykeion (Lyzeum), das zur Akademie in Konkurrenz stand. Nach dem Tod Alexanders, zwölf Jahre später, wurde Athen wieder antimakedonisch, und Aristoteles zog sich auf seinen Familienbesitz in Chalkis zurück, wo er 322 v. Chr. starb.

Hauptwerke

um 350 v. Chr. Analytica Priora; Analytica Posteriora; De Interpretatione

335–323 v. Chr. Nikomachische Ethik; 335–323 v. Chr. Politik

IM KONTEXT

SCHLÜSSELFIGUR

Euklid(um 300 v. Chr.)

TEILGEBIET

Geometrie

FRÜHER

um 600 v. Chr.Der griechische Philosoph, Mathematiker und Astronom Thales von Milet beweist, dass Kreiswinkel am Halbkreisbogen stets rechte Winkel sind. (Später Lehrsatz 31 in Euklids Elementen .)

um 440 v. Chr.Der griechische Mathematiker Hippokrates von Chios schreibt das erste systematische Geometrielehrbuch Stoicheia (»Elemente«).

SPÄTER

um 1820entwickeln Mathematiker wie Carl Friedrich Gauss, János Bolyai und Nikolai Iwanowitsch Lobatschewski die nichteuklidische hyperbolische Geometrie.

Euklids Elemente dürfte das einflussreichste mathematische Werk aller Zeiten sein. Es dominierte die Konzepte der Menschen von Raum und Zahl über 2000 Jahre lang und diente bis Anfang des 20. Jahrhunderts als Standardlehrbuch der Geometrie.

Euklid lebte in Alexandria (Ägypten) um 300 v. Chr. Die Stadt war damals Teil der griechischsprachigen hellenistischen Welt, die im ganzen Mittelmeerraum erblühte. Er hatte wohl auf nicht beständigem Papyrus geschrieben, da alles, was von seinem Werk erhalten ist, Kopien, Übersetzungen und Kommentare sind, die spätere Gelehrte anfertigten.

Die Elemente (gr.: Stoicheia ) ist eine Sammlung von 13 Büchern, die ein breites Themenspektrum abdecken. Bücher I bis IV behandeln die ebene Geometrie, also ebene Flächen. Buch V diskutiert Brüche und Verhältnisse, inspiriert von der Arbeit des griechischen Mathematikers und Astronomen Eudoxos von Knidos. Buch VI enthält fortgeschrittenere ebene Geometrie. Bücher VII bis IX widmen sich der Zahlentheorie; darin werden Eigenschaften und Beziehungen von Zahlen diskutiert. Das lange und schwierige Buch X untersucht inkommensurable Zahlen, die »Unmessbaren«, heute irrationale Zahlen genannt, die sich nicht als Bruch aus Ganzzahlen darstellen lassen. Bücher XI bis XIII erkunden die Geometrie dreidimensionaler Festkörper.

»Es gibt keinen Königsweg zur Geometrie. «

Euklidzitiert in: Proklos: Kommentar zu Euklids Elementen , 5. Jh. n. Chr.

Buch XIII der Elemente wird eigentlich einem anderen Autor zugeschrieben: Theaitetos, einem athenischen Mathematiker und Schüler Platons, der 369 v. Chr. starb. Das Buch behandelt die fünf regulären konvexen Polyeder – Tetraeder, Würfel, Oktaeder, Dodekaeder und Ikosaeder – die platonischen Körper. Es ist das erste dokumentierte Beispiel eines Klassifikationstheorems. Eines, das alle möglichen Körper auflistet, die bestimmte Bedingungen erfüllen.