John Farndon - Big Ideas. Das Mathematik-Buch

Zwar bezweifeln Historiker die Geschichte der Schmiede, aber Pythagoras wird allgemein eine andere musikalische Entdeckung zugeschrieben. Er soll mit Tönen verschieden langer Lyrasaiten experimentiert haben. Erzeugt eine Saite einen Ton der Frequenz f , dann, fand Pythagoras, erzeugt eine Saite der halben Länge einen Ton eine Oktave höher, also der Frequenz 2 f . Als Pythagoras die gleichen Verhältnisse der harmonischen Hämmer auf die Saiten anwandte, entstanden wiederum Noten, die miteinander harmonierten. Pythagoras konstruierte daraus eine Tonleiter, beginnend mit einer Note und der gleichen Note eine Oktave höher, und füllte sie mit Noten im Abstand reiner Quinten.

Diese Tonleiter verwendete man bis ins 18. Jahrhundert, bis die gleichstufige Tonleiter sie ablöste. Zwar funktionierte die pythagoreische Stimmung gut für Musik innerhalb einer Oktave, war aber weniger für modernere Musik geeignet, die verschiedene Grundtöne und einen Tonumfang über mehrere Oktaven verwendete. Zwar gibt es viele Arten von Tonleitern in verschiedenen Kulturen, doch die lange Tradition der westlichen Musik geht bis auf die Pythagoreer und ihre Suche nach der Beziehung zwischen Musik und mathematischen Verhältnissen zurück.

Pythagoras’ Ruf als berühmtester Mathematiker der Antike ist durch seine Beiträge zur Geometrie, Zahlentheorie und Musik gerechtfertigt. Seine Arbeit beruhte nicht immer nur auf seinen eigenen Ideen, aber die Rigorosität, mit der er und seine Anhänger sie entwickelten und mithilfe von Axiomen und Logik ein mathematisches System aufbauten, war ein bedeutendes Erbe für seine Nachfolger.

»Es gibt Geometrie in dem Tönen der Saiten, es gibt Musik in den Abständen der Sphären. «

Pythagoras

Pythagoreische Tripel

Ein Tupel aus drei natürlichen Zahlen, das die Gleichung a 2+ b 2= c 2löst, nennt man ein pythagoreisches Tripel (auch wenn ihre Existenz lange vor Pythagoras bekannt war). Um 1800 v. Chr. hielten Babylonier auf der Tontafel Plimpton 322 eine Tabelle mit pythagoreischen Tripeln fest. Sie zeigt: je größer die Zahlen, desto seltener die Tripel. Die Pythagoreer entwickelten Methoden, um neue Tripel zu finden. Sie bewiesen zudem, dass es unendlich viele gibt. Nach der Zerstörung pythagoreischer Schulen in den politischen Säuberungen des 6. Jh. v. Chr. wanderten viele Pythagoreer in andere Gegenden Süditaliens aus und verbreiteten ihr Wissen in der antiken Welt. Zwei Jahrhunderte später fand Euklid eine Formel: a = m 2– n 2, b = 2 mn, c = m 2+ n 2. Dabei sind m und n zwei beliebige natürliche Zahlen (mit m > n ). 7 und 4 bilden etwa das Tripel (33, 56, 65), mit 33 2+ 56 2= 65 2. Die Formel machte die Suche nach Tripeln erheblich einfacher und schneller.

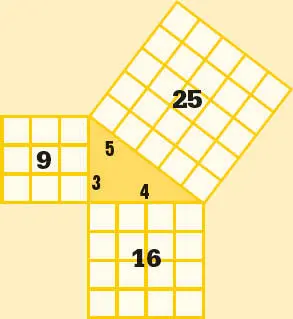
Das kleinstepythagoreische Tripel ist (3, 4, 5). Wie die Grafik zeigt, gilt für die Quadrate 9 + 16 = 25.

Pythagoras

Pythagoras wurde auf der griechischen Insel Samos in der Ostägäis um 570 v. Chr. geboren. Er beeinflusste viele große Gelehrte der Geschichte, von Platon, Nikolaus Kopernikus, Johannes Kepler bis zu Isaac Newton. Pythagoras war weit gereist und übernahm Ideen von Gelehrten in Ägypten und dem Nahen Osten, bevor er um 518 v. Chr. eine Gemeinschaft mit etwa 600 Mitgliedern in Kroton (heutiges Crotone) in Kalabrien (Süditalien) gründete. Die asketische Gruppe forderte ein Streben nach intellektuellen Erkenntnissen, hatte aber auch strikte Ernährungs- und Kleidungsregeln. Irgendwann ab dieser Zeit dürften seine Sätze und Entdeckungen formuliert worden sein, doch Details sind nicht erhalten. Mit 60 Jahren soll er ein junges Gemeindemitglied, Theano, geheiratet haben, mit der er zwei oder drei Kinder hatte. Politische Unruhen in Kroton führten zu Verfolgungen der Pythagoreer, und Pythagoras selbst könnte umgekommen sein, als die Schule in Brand gesetzt wurde, oder kurz danach. Er soll um 495 v. Chr. gestorben sein.

IM KONTEXT

SCHLÜSSELFIGUR

Hippasos(5. Jh. v. Chr.)

TEILGEBIET

Zahlensysteme

FRÜHER

19. Jh. v. Chr.Die Babylonier konstruieren rechtwinklige Dreiecke und verstehen ihre Eigenschaften, wie Keilschrifttafeln zeigen.

6. Jh. v. Chr.In Griechenland wird die Beziehung zwischen den Seitenlängen von rechtwinkligen Dreiecken entdeckt. Man schreibt sie später Pythagoras zu.

SPÄTER

400 v. Chr.Theodoros von Kyrene beweist die Irrationalität der Quadratwurzeln der Nichtquadratzahlen zwischen 3 und 17.

4. Jh. v. Chr.Der Grieche Eudoxos von Knidos legt klare mathematische Grundlagen für irrationale Zahlen fest.

Jede Zahl, die sich als Verhältnis zweier ganzer Zahlen – also als Bruch – ausdrücken lässt, nennt man rationale Zahl. Als Dezimalzahl geschrieben haben rationale Zahlen entweder endlich viele Nachkommastellen, oder die Abfolge der Nachkommastellen wiederholt sich. Dagegen kann man irrationale Zahlen nicht als endlichen Bruch darstellen.

Der griechische Gelehrte Hippasos soll im 5. Jh. v. Chr. bei der Arbeit an geometrischen Problemen erstmals irrationale Zahlen entdeckt haben. Er kannte den Satz von Pythagoras, nach dem das Quadrat der Hypotenuse (längste Seite) eines rechtwinkligen Dreiecks gleich der Summe der Quadrate der anderen zwei Seiten ist. Wendet man dies auf ein Dreieck an, bei dem beide kurzen Seiten die Länge 1 haben, gilt 1 2+ 1 2= 2. Die Länge der Hypotenuse ist dann die Quadratwurzel von 2.

Die Quadratwurzel von 2 kann jedoch nicht als Bruch zweier ganzer Zahlen geschrieben werden. Es gibt keine zwei ganzen Zahlen, deren Verhältnis quadriert wieder 2 ergibt. Daher ist die Quadratwurzel von 2 keine rationale Zahl. Solche Zahlen heißen irrationale Zahlen. Die 2 ist also keine Quadratzahl, genauso wie die Zahlen 3, 5, 7 und viele andere, ihre Quadratwurzeln sind daher alle irrational. Dagegen sind 4 (= 2 2), 9 (= 3 2) und 16 (= 4 2) Quadratzahlen. Ihre Quadratwurzeln sind natürliche Zahlen und damit rational.

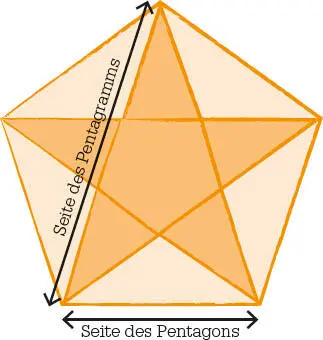
Hippasos könnteauf irrationale Zahlen gestoßen sein, als er das Verhältnis zwischen den Seitenlängen eines Pentagons und eines eingeschriebenen Pentagramms erforschte. Er stellte fest, dass sich das Verhältnis nicht als Bruch zweier ganzer Zahlen ausdrücken ließ.

Das Konzept irrationaler Zahlen wurde nicht sofort allgemein akzeptiert, obgleich spätere griechische und indische Mathematiker ihre Eigenschaften untersuchten. Im 9. Jahrhundert verwendeten arabische Gelehrte sie in der Algebra.