John Farndon - Big Ideas. Das Mathematik-Buch

Man weiß, dass Euklid auch über Kegelschnitte geschrieben hat, aber diese Arbeiten sind nicht mehr erhalten. Kegelschnitte sind z. B. Kreise, Ellipsen, Parabeln und Hyperbeln. Sie entstehen, wenn eine Ebene einen hohlen Kegel schneidet.

Der Titel von Euklids Werk hat eine bestimmte Bedeutung, die seinen mathematischen Zugang reflektiert. Im 20. Jahrhundert meinte der britische Mathematiker John Fauvel, das griechische Wort für »Element«, stoicheion , habe mit der Zeit die Bedeutung geändert: von »Bestandteil einer Reihe« (etwa ein Baum in einer Baumreihe) zu »Satz, mit dem man andere beweisen kann« und schließlich »Anfangspunkt für viele Lehrsätze«. In diesem Sinn verwendete es Euklid. Der Grieche Proklos verglich im 5. Jahrhundert n. Chr. Elemente mit »Buchstaben«, denn Kombinationen von Buchstaben erzeugen Wörter, so wie Kombinationen von Axiomen – Aussagen, die als offensichtlich wahr gelten – Lehrsätze erzeugen.

Euklid schrieb nicht in Isolation, sondern er baute auf den Grundlagen vieler einflussreicher griechischen Mathematiker auf. Thales von Milet, Hippokrates von Chios, Platon und andere hatten sich bereits der mathematischen Denkweise genähert, die Euklid brillant formalisierte: die Welt der Beweise. Sie macht Euklid einzigartig. Seine Schriften sind die ältesten erhaltenen Beispiele für vollständig axiomatische Mathematik. Er identifizierte bestimmte grundlegende Fakten und leitete davon in sich korrekte, logische Aussagen (Propositionen) ab. Euklid sammelte zudem das gesamte mathematische Wissen seiner Zeit und gliederte es in einem strukturierten mathematischen System, das die bewiesenen Zusammenhänge zwischen den verschiedenen Propositionen sorgfältig erklärte.

Diese Anfangsseite von Euklids Elementen zeigt den illuminierten (mit Buchmalerei versehenen) Text mit Diagrammen der ersten gedruckten Ausgabe, produziert 1482 in Venedig.

Euklid stand vor einer Herkulesaufgabe, die Mathematik seiner Zeit zu systematisieren. Sein axiomatisches System begann er mit 23 Definitionen für Begriffe wie Punkt, Linie, Fläche, Kreis und Durchmesser. Dann stellte er fünf Postulate auf: man kann zwei Punkte zu einer Strecke verbinden; man kann jede Strecke unendlich zu einer Geraden verlängern; jede Strecke kann Radius eines Kreises sein; alle rechten Winkel sind gleich zueinander, sowie ein Postulat über Parallelen.

Dann folgten fünf Axiome (als wahr akzeptierte Grundsätze): Wenn A = B und B = C , dann A = C ; wenn A = B und C = D , dann A + C = B + D ; wenn A = B und C = D , dann A – C = B – D ; wenn A und B übereinstimmen, dann sind A und B gleich; und das Ganze von A ist größer als ein Teil von A .

Euklids fünf Postulate

1.Zwischen zwei beliebigen Punkten kann man eine Strecke (gerade Linie) ziehen.

2.Jede Strecke (begrenzte gerade Linie) kann man unendlich gerade verlängern.

3.Zu jedem beliebigen vorgegebenen Mittelpunkt und Radius kann man einen Kreis zeichnen.

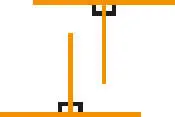
4.Alle rechten Winkel sind zueinander gleich.

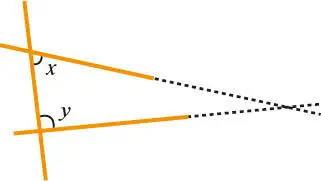
5.Ist die Summe der Winkel x + y kleiner als zwei rechte Winkel, so schneiden sich die Geraden irgendwo seitlich davon.

Um für Satz 1 ein gleichseitiges Dreieck über einer Strecke zu konstruieren, nannte Euklid die Endpunkte der Strecke A und B (siehe unten). Dann zog er um diese Punkte je einen Kreis mit dem Radius AB – unter Ausnutzung des dritten Postulats. Den Schnittpunkt der Kreise nannte er C . Aufgrund des ersten Postulats konnte er nun die Strecken AC und BC zeichnen. Da die Radien der beiden Kreise gleich der Länge von [AB] sind, gilt AC = AB und BC = AB ; nach Euklids erstem Axiom gilt damit auch AC = BC , womit er ein gleichseitiges Dreieck über der Strecke AB konstruiert hat.

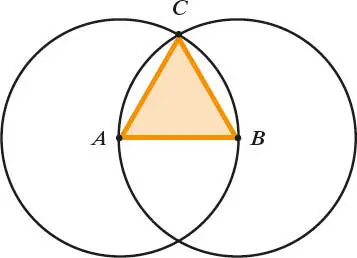
Um ein gleichseitiges Dreieckfür Satz 1 zu konstruieren, zeichnete Euklid eine Strecke und Kreise um jeden ihrer beiden Endpunkte A und B . Mit dem Schnittpunkt C der Kreise ergab sich ein Dreieck mit gleich langen Seiten AB, AC und BC .

In lateinischen Übersetzungen der Elemente endeten Konstruktionen mit den Buchstaben QEF ( quod erat faciendum , »was zu machen war«) und logische Beweise mit QED ( quod erat demonstrandum , »was zu zeigen war«).

Die Konstruktion des gleichseitigen Dreiecks ist ein gutes Beispiel für Euklids Methode. Jeder Schritt wird durch Bezug auf die Definitionen, Postulate und Axiome begründet. Nichts anderes kann angenommen werden; intuitive Aussagen sind fehlerverdächtig. Euklids erster Satz wurde von späteren Gelehrten kritisiert. So hat Euklid die Existenz des Schnittpunkts C nicht begründet oder erklärt. Zwar ist sie offensichtlich, ist aber nicht aus den Annahmen ableitbar. Postulat 5 erwähnt zwar einen Schnittpunkt, aber von zwei Geraden, nicht von Kreisen. In ähnlicher Weise beschreibt eine der Definitionen ein Dreieck als eine ebene Form, begrenzt von drei Strecken, die alle in einer Ebene liegen. Doch Euklid scheint niemals explizit gezeigt zu haben, dass die Strecken AB, BC und CA tatsächlich in einer Ebene liegen.

Postulat 5 heißt auch »Parallelenpostulat«, da man mit ihm Eigenschaften paralleler Geraden beweisen kann: wenn eine Gerade zwei weitere Geraden g und h so schneidet, dass die dadurch gebildeten zugewandten Winkel auf einer der beiden Seiten in der Summe kleiner als 180 ° sind, dann schneiden sich die Geraden g und h irgendwo auf dieser Seite. Euklid verwendet dieses erst in Satz 29, indem er beweist: Werden zwei parallele Geraden von einer Geraden geschnitten, dann sind jeweils zwei nebeneinanderliegende Winkel einer Geradenkreuzung (Nebenwinkel) gleich 180 °. Das fünfte Postulat ist komplizierter als die anderen, und Euklid schien selbst damit unzufrieden gewesen zu sein.