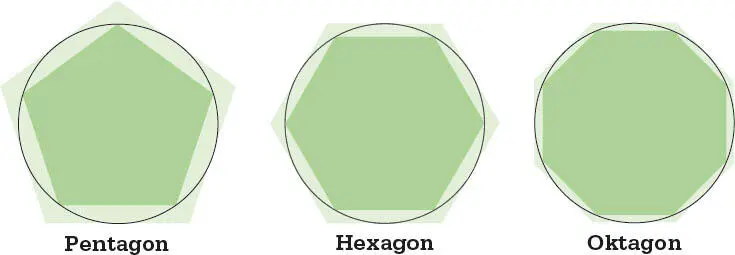
Zwar benutzte man Polygonumfängeschon lange zur Näherung des Kreisumfangs, aber Archimedes verwendete als Erster eingeschriebene (im Kreis liegende) und umschriebene (den Kreis bedeckende) Polygone für untere und obere Grenzen.
Ein anderer Weg zur Abschätzung von π , die »Quadratur des Kreises«, war unter den altgriechischen Mathematikern eine beliebte Herausforderung. Es geht darum, nur mit Zirkel und Lineal ein Quadrat zu konstruieren, das dieselbe Fläche wie ein gegebener Kreis hat. Aus dem Wissen über die Fläche eines Quadrats könnte man dann die Kreisfläche annähern. Die Griechen hatten damit keinen Erfolg, und im 19. Jahrhundert wurde letztlich bewiesen, dass die Quadratur des Kreises unmöglich ist, weil π eine transzendente Zahl ist. Auch heute noch bezeichnet man daher unmögliche Vorhaben als »Quadratur des Kreises«. Ein anderer Versuch der »Quadratur des Kreises« zerlegt den Kreis in Segmente und legt sie in Parallelogrammform aus (siehe unten). Die Fläche des Parallelogramms ist (ungefähr) r · ½ (2 πr ) = r · πr = πr 2, wobei r der Radius des Kreises und 2 πr sein Umfang ist. Damit ist die Kreisfläche ebenfalls πr 2, und je dünner die Segmente sind, desto besser nähern sie sich dem Parallelogramm an.
»Die Abhandlungen [von Archimedes] sind ohne Ausnahme Monumente der mathematischen Darstellung. «
Thomas L. HeathBritischer Mathematikhistoriker A History Of Greek Mathematics , 1921
Über 300 Jahre nach Archimedes’ Tod bestimmte Ptolemäus (um 100–170 n. Chr.) π als 3,8.30 (als Sexagesimalzahl geschrieben), also 3 + 8/ 60+ 30/ 3600= 3,141666… was nur 0,002 % größer als der heutige Wert ist. In China wurde oft 3 für π verwendet und ab dem 2. Jahrhundert war  üblicher (etwa 0,7 % zu groß). Wang Fau erklärte im 3. Jahrhundert, ein Kreis vom Umfang 142 habe den Durchmesser 45. Demnach wäre π etwa 142/ 45= 3,1555…, 0,4 % zu groß. Zugleich schätzte Liu Hui π mit 3072-seitigen Polygonen auf 3,1416. Im 5. Jahrhundert nahmen Zu Chongzi und sein Sohn ein 12 288-seitiges Polygon und fanden die Näherung 355/ 113= 3,14159292… Das ist auf sechs Nachkommastellen richtig. Diese Genauigkeit erreichte man in Europa erst im 16. Jahrhundert. In Indien beschrieb Aryabhata in dem mathematisch-astronomischen Werk Aryabhatiya von 499 n. Chr. die Berechnung von π : »Addiere 4 zu 100, multipliziere mit 8, dann addiere 62 000. Mit dieser Regel kann die Berechnung des Umfangs eines Kreises mit dem Durchmesser 20 000 angegangen werden«. Es ergibt für π den Wert [8 · (100 + 4) + 62 000] : 20 000 = 62 832 : 20 000 = 3,1416.
üblicher (etwa 0,7 % zu groß). Wang Fau erklärte im 3. Jahrhundert, ein Kreis vom Umfang 142 habe den Durchmesser 45. Demnach wäre π etwa 142/ 45= 3,1555…, 0,4 % zu groß. Zugleich schätzte Liu Hui π mit 3072-seitigen Polygonen auf 3,1416. Im 5. Jahrhundert nahmen Zu Chongzi und sein Sohn ein 12 288-seitiges Polygon und fanden die Näherung 355/ 113= 3,14159292… Das ist auf sechs Nachkommastellen richtig. Diese Genauigkeit erreichte man in Europa erst im 16. Jahrhundert. In Indien beschrieb Aryabhata in dem mathematisch-astronomischen Werk Aryabhatiya von 499 n. Chr. die Berechnung von π : »Addiere 4 zu 100, multipliziere mit 8, dann addiere 62 000. Mit dieser Regel kann die Berechnung des Umfangs eines Kreises mit dem Durchmesser 20 000 angegangen werden«. Es ergibt für π den Wert [8 · (100 + 4) + 62 000] : 20 000 = 62 832 : 20 000 = 3,1416.
»Es gibt kein Ende bei Pi. Ich würde es gerne mit mehr Ziffern versuchen. «
Emma Haruka IwaoJapanische Informatikerin Woman Smashes Pi World Record , BBC, 14 März 2019
Brahmagupta (um 598–668) leitete Quadratwurzelnäherungen für π mithilfe von regulären Polygonen mit 12, 24, 48 und 96 Ecken ab: 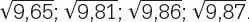 . Auf vier Nachkommastellen fand er π 2= 9,8696, sodass er als Näherung π =
. Auf vier Nachkommastellen fand er π 2= 9,8696, sodass er als Näherung π =  vorschlug. Im 9. Jahrhundert verwendete der in Bagdad lebende al-Chwarizmi 3 1/ 7,
vorschlug. Im 9. Jahrhundert verwendete der in Bagdad lebende al-Chwarizmi 3 1/ 7,  und 62 832/ 20 000als Näherungen für π . Den ersten Wert schrieb er griechischen, die anderen beiden indischen Quellen zu. Der englische Gelehrte Adelard von Bath übersetzte im 12. Jahrhundert Werke von al-Chwarizmi ins Lateinische, was in Europa das Interesse an π aufleben ließ. 1220 berechnete Leonardo von Pisa (Fibonacci), der im Liber Abbaci (»Buch der Rechenkunst«, 1202) die indisch-arabischen Zahlen in Europa populär gemacht hatte, π als 864/ 275= 3,141818…, eine kleine Verbesserung gegenüber der Näherung von Archimedes, aber nicht so genau wie die von Ptolemäus, Zu Chongzhi oder Aryabhata. Zwei Jahrhunderte später plante Leonardo da Vinci (1452–1519) ein Rechteck mit der Länge eines Kreisumfangs und Höhe seines halben Radius, um die Kreisfläche zu bestimmen.
und 62 832/ 20 000als Näherungen für π . Den ersten Wert schrieb er griechischen, die anderen beiden indischen Quellen zu. Der englische Gelehrte Adelard von Bath übersetzte im 12. Jahrhundert Werke von al-Chwarizmi ins Lateinische, was in Europa das Interesse an π aufleben ließ. 1220 berechnete Leonardo von Pisa (Fibonacci), der im Liber Abbaci (»Buch der Rechenkunst«, 1202) die indisch-arabischen Zahlen in Europa populär gemacht hatte, π als 864/ 275= 3,141818…, eine kleine Verbesserung gegenüber der Näherung von Archimedes, aber nicht so genau wie die von Ptolemäus, Zu Chongzhi oder Aryabhata. Zwei Jahrhunderte später plante Leonardo da Vinci (1452–1519) ein Rechteck mit der Länge eines Kreisumfangs und Höhe seines halben Radius, um die Kreisfläche zu bestimmen.
Archimedes’ Polygonmethode war auch im späten 16. Jahrhundert noch beliebt. 1579 verwendete der französische Mathematiker François Viète 393 reguläre Polygone mit je 216 Seiten, um π auf 10 Dezimalstellen genau zu berechnen. 1593 bestimmte der flämische Mathematiker Adriaan van Roomen (Romanus) π mit einem 230-seitigen Polygon auf 17 Stellen genau. Drei Jahre später berechnete der deutsch-niederländische Mathematikprofessor Ludolph van Ceulen π auf 35 Stellen. Sein Ergebnis ist als »ludolphsche Zahl« bekannt.
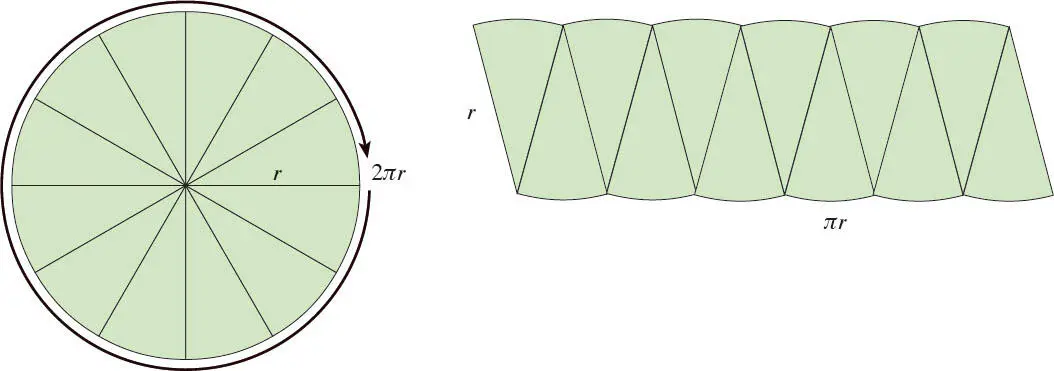
Wenn man die Kreissegmenteparallelogrammförmig aneinanderlegt, kann man zeigen, dass die Fläche des Kreises πr 2ist. Die Höhe des Parallelogramms ist annähernd gleich dem Kreisradius r , und seine Breite ist annähernd die Hälfte des Umfangs (2 πr ), also πr .

Das Verhältnis von Umfang zu Höheder Großen Pyramide von Gizeh (Ägypten) ist fast genau π , was bedeuten könnte, dass ihre Baumeister sich der Zahl bewusst waren.
Die Reihenentwicklung des Arcustangens durch den schottischen Astronomen und Mathematiker James Gregory 1671 und unabhängig 1674 durch Gottfried Leibniz war ein neuer Zugang zur Berechnung von π . Er ist die Umkehrfunktion des Tangens. Ein Vollkreis entspricht im Bogenmaß (Radiant) 2 π , daher ermöglichte die Reihenentwicklung seine Berechnung.
Leider sind Hunderte von Reihengliedern nötig, um π auch nur auf wenige Stellen genau zu berechnen. Viele Mathematiker führten die Berechnung mit der Arcustangensfunktion durch, darunter Leonhard Euler im 18. Jahrhundert. Schließlich berechnete der Brite William Rutherford 208 Stellen von π mit der Arcustangensreihe.
Die Entwicklung elektronischer Computer im 20. Jahrhundert vereinfachte die Berechnung. 1949 wurden 2037 Stellen innerhalb von 70 Stunden berechnet. Vier Jahre später dauerte es nur noch etwa 13 Minuten, um 3089 Stellen zu bestimmen. 1961 berechneten die US-Amerikaner Daniel Shanks und John Wrench mit der Arcustangensreihe 100 625 Stellen von π in weniger als acht Stunden. 1973 schafften die Franzosen Jean Guillaud und Martin Bouyer eine Million Stellen, und 1989 erreichten die ukrainisch-amerikanischen Brüder David und Gregory Chudnovsky eine Milliarde Dezimalstellen von π .
Читать дальше


 üblicher (etwa 0,7 % zu groß). Wang Fau erklärte im 3. Jahrhundert, ein Kreis vom Umfang 142 habe den Durchmesser 45. Demnach wäre π etwa 142/ 45= 3,1555…, 0,4 % zu groß. Zugleich schätzte Liu Hui π mit 3072-seitigen Polygonen auf 3,1416. Im 5. Jahrhundert nahmen Zu Chongzi und sein Sohn ein 12 288-seitiges Polygon und fanden die Näherung 355/ 113= 3,14159292… Das ist auf sechs Nachkommastellen richtig. Diese Genauigkeit erreichte man in Europa erst im 16. Jahrhundert. In Indien beschrieb Aryabhata in dem mathematisch-astronomischen Werk Aryabhatiya von 499 n. Chr. die Berechnung von π : »Addiere 4 zu 100, multipliziere mit 8, dann addiere 62 000. Mit dieser Regel kann die Berechnung des Umfangs eines Kreises mit dem Durchmesser 20 000 angegangen werden«. Es ergibt für π den Wert [8 · (100 + 4) + 62 000] : 20 000 = 62 832 : 20 000 = 3,1416.
üblicher (etwa 0,7 % zu groß). Wang Fau erklärte im 3. Jahrhundert, ein Kreis vom Umfang 142 habe den Durchmesser 45. Demnach wäre π etwa 142/ 45= 3,1555…, 0,4 % zu groß. Zugleich schätzte Liu Hui π mit 3072-seitigen Polygonen auf 3,1416. Im 5. Jahrhundert nahmen Zu Chongzi und sein Sohn ein 12 288-seitiges Polygon und fanden die Näherung 355/ 113= 3,14159292… Das ist auf sechs Nachkommastellen richtig. Diese Genauigkeit erreichte man in Europa erst im 16. Jahrhundert. In Indien beschrieb Aryabhata in dem mathematisch-astronomischen Werk Aryabhatiya von 499 n. Chr. die Berechnung von π : »Addiere 4 zu 100, multipliziere mit 8, dann addiere 62 000. Mit dieser Regel kann die Berechnung des Umfangs eines Kreises mit dem Durchmesser 20 000 angegangen werden«. Es ergibt für π den Wert [8 · (100 + 4) + 62 000] : 20 000 = 62 832 : 20 000 = 3,1416.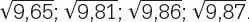 . Auf vier Nachkommastellen fand er π 2= 9,8696, sodass er als Näherung π =
. Auf vier Nachkommastellen fand er π 2= 9,8696, sodass er als Näherung π = 












