John Farndon - Big Ideas. Das Mathematik-Buch

2016 setzte der Schweizer Teilchenphysiker Peter Trüb das Programm y-Cruncher auf Hochleistungscomputern ein und berechnete 22,4 Billionen Stellen. Ein neuer Weltrekord (ebenfalls mit y-Cruncher ) wurde dann von Emma Haruka Iwai im März 2019 mit über 31 Billionen Stellen erreicht.

Archimedes

Der 287 v. Chr. in Syrakus (Sizilien) geborene Universalgelehrte Archimedes war ein brillanter Mathematiker und Erfinder, der für den Ausruf »Heureka« berühmt ist, als er erkannte, dass das Volumen eines Gegenstands gleich dem des von ihm verdrängten Wassers ist. Eine ihm zugeschriebene Erfindung ist die archimedische Schraube oder Schneckenpumpe, eine rotierende Spiralwendel, die Wasser einen Hang hinauftransportiert.

In der Mathematik nutzte er praktische Verfahren, um zu beweisen, dass das Volumen von Zylinder, Kugel und Kegel (gleicher Höhen und Durchmesser) 3:2:1 ist. Einigen gilt er als Vorreiter der Infinitesimalrechnung, die erst im 17. Jahrhundert entwickelt wurde. Er wurde 212 v. Chr. bei der Belagerung von Syrakus von römischen Soldaten getötet – trotz des Befehls, ihn zu verschonen.

Hauptwerke

um 250 v. Chr. Kyklou metresis (Kreismessung)

um 225 v. Chr. Peri sphairas kai kylindrou (Über Kugel, Zylinder); Peri elikon (Über Spiralen)

Anwendungen von Pi

Weltraumforscher brauchen π in ihren Berechnungen ständig. So kann man die Länge der Umlaufbahn eines Satelliten über der Planetenoberfläche nach einem grundlegenden Prinzip berechnen. Dafür multipliziert man π mit dem bekannten Durchmesser und erhält den Kreisumfang. Beispielsweise berechneten NASA-Wissenschaftler 2015 so die Zeit, die die Sonde Dawn für einen Umlauf um Ceres braucht, einem Zwergplaneten im Asteroidengürtel zwischen Mars und Jupiter.

Als Forscher am Jet Propulsion Laboratory der NASA bestimmen wollten, wie viel Wasserstoff an der Oberfläche von Europa, dem kleinsten Jupitermond, austritt, ermittelten sie zunächst, wie viel Wasserstoff insgesamt durch chemische Reaktionen im Gestein entsteht. Diesen Wert teilten sie dann durch die Oberfläche des Mondes: 4 πr 2, (wie für jede Kugel) mit dem bekannten Mondradius r . Man kann mit π auch einfach berechnen, welche Distanz ein Mensch bei einer Umdrehung der Erde zurücklegt, wenn man den Breitengrad kennt, auf dem er sich befindet.

Astrophysiker brauchen π für die Berechnung der Umlaufbahnen und der Merkmale von Himmelskörpern wie dem Planeten Saturn.

IM KONTEXT

SCHLÜSSELFIGUR

Eratosthenes(um 276–194 v. Chr.)

TEILGEBIET

Zahlentheorie

FRÜHER

um 1500 v. Chr.Die Babylonier unterscheiden zwischen Primzahlen und zusammengesetzten Zahlen.

um 300 v. Chr.In den Elementen (Buch IX, Lehrsatz 20) beweist Euklid, dass es unendlich viele Primzahlen gibt.

SPÄTER

Frühes 19. Jh.Carl Friedrich Gauß und Adrien-Marie Legendre stellen unabhängig eine Vermutung über die Dichte von Primzahlen auf.

1859Bernhard Riemann stellt eine Vermutung über die Verteilung der Primzahlen auf. Mit ihr hat man viele andere Sätze bewiesen, aber die Vermutung selbst ist noch unbewiesen.

Neben der Berechnung des Umfangs der Erde und der Entfernung des Mondes von der Erde fand der griechische Universalgelehrte Eratosthenes eine Methode, um Primzahlen zu finden. Primzahlen – natürliche Zahlen, die nur durch 1 und sich selbst teilbar sind – hatten Mathematiker seit Jahrhunderten fasziniert. Sein »Sieb« – bei dem in einer Zahlentabelle alle Vielfachen von 2, 3, 5 und den anderen bekannten Primzahlen durchstreicht – machte sie deutlich leichter zugänglich.

Primzahlen haben genau zwei Faktoren: 1 und sich selbst. Die Griechen verstanden die Primzahlen als »Bausteine« für natürliche Zahlen. In den Elementen nannte Euklid viele Eigenschaften von Primzahlen und zusammengesetzten Zahlen (die durch Multiplikation mehrerer Zahlen entstehen). Etwa, dass jede natürliche Zahl entweder selbst eine Primzahl oder das Produkt von Primzahlen (den »Primfaktoren«) ist. Einige Jahrzehnte später fand Eratosthenes ein Verfahren, um theoretisch beliebig große Primzahlen zu finden, indem Vielfache bekannter Primzahlen in einem Zahlengitter, etwa von 1 bis 100 (siehe oben), »ausgesiebt« werden. Da 1 nicht als Primzahl gilt, ist 2 die erste Primzahl (und die einzige gerade). Alle anderen geraden Zahlen sind durch 2 teilbar und werden gestrichen. Damit müssen alle weiteren Primzahlen ungerade sein. Die nächste Zahl, 3, hat (außer 1 und sich selbst) keine Faktoren und ist daher prim; ihre Vielfachen aber sind nicht prim und werden ebenfalls gestrichen. Die Zahl 4 = 2 · 2 und ihre Vielfachen sind bereits gestrichen, da sie auch Vielfache von 2 sind. 5 ist wieder prim, ihre Vielfachen aber nicht. 6 und ihre Vielfachen sind bereits (als Vielfache von 2 und 3) ausgestrichen. 7 ist wieder prim, sodass man ihre noch nicht ausgestrichenen Vielfachen 49, 77 und 91 entfernt. Die Vielfachen von 8, 9 und 10 sind bereits entfernt (da sie auch Vielfache von 2, 3 oder 5 sind). Unter den Zahlen bis 100 sind die Vielfachen von 11 und größerer Primzahlen auch bereits entfernt (da sie kleinere Primfaktoren enthalten). Damit bleiben nur 25 Primzahlen unter 100, die man alle nur durch Entfernen der Vielfachen von 2, 3, 5 und 7 identifiziert hat.

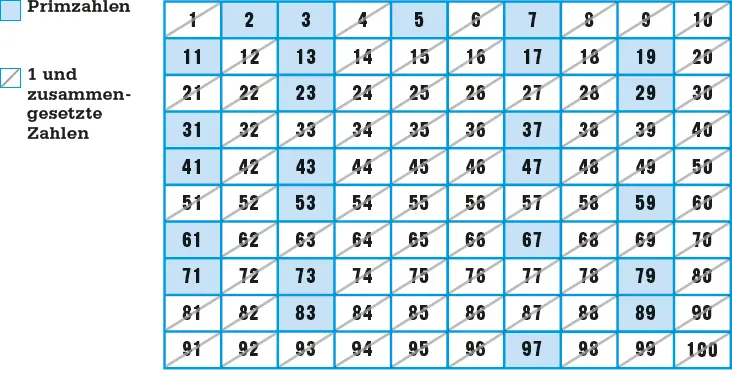
Eratosthenes’ Methode beginntmit einer Tabelle eines Zahlenbereichs. Zuerst streicht man die 1 aus, dann alle Vielfachen von 2, mit Ausnahme der 2 selbst. Ebenso geht man mit den Vielfachen von 3, 5 und 7 vor. Vielfache von Zahlen größer wie 7 sind bereits ausgestrichen (z. B. 8, 9, 10 sind Vielfache von 2, 3, 5).

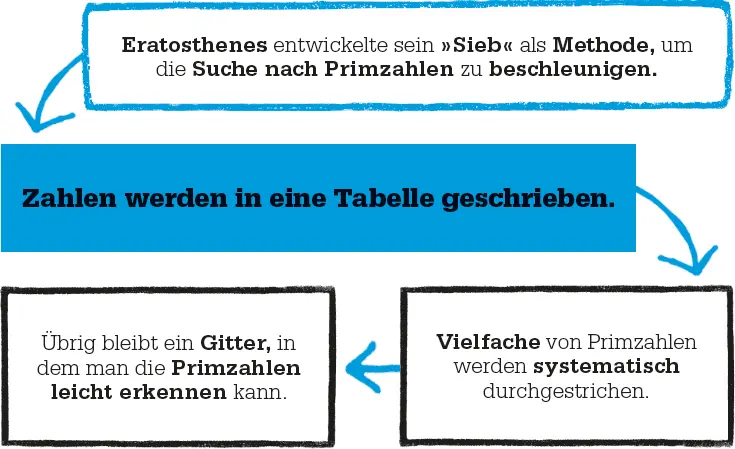
Primzahlen haben die Aufmerksamkeit von Mathematikern seit dem 17. Jahrhundert erregt, als Gelehrte wie Pierre de Fermat, Marin Mersenne, Leonhard Euler und Carl Friedrich Gauß ihre Eigenschaften genauer erforschten.

Selbst im Computerzeitalter ist es enorm aufwendig festzustellen, welche Primfaktoren eine große Zahl hat. So beruht die Verschlüsselung mit öffentlichem Schlüssel – die Basis der sicheren Internetkommunikation – auf der Wahl zweier sehr großer Primzahlen. Hacker müssten die Primfaktorzerlegung riesiger Zahlen berechnen. Sollte dies praktikabel werden, wären neue Verschlüsselungsmethoden nötig.