John Farndon - Big Ideas. Das Mathematik-Buch

Im 12. Jahrhundert begründete der Inder Bhaskara II. die sphärische Trigonometrie, die Dreiecke und andere Formen auf einer Kugeloberfläche (statt in der Ebene) erforscht.

In späteren Zeiten war die Trigonometrie in der Navigation und Astronomie unschätzbar wertvoll. Die Arbeiten von Bhaskara II. sowie der Almagest von Ptolemäus wurden von islamischen Gelehrten im Mittelalter, die sich bereits lange vor Bhaskara II. mit Trigonometrie beschäftigten, hoch geschätzt.

Parallel zur Entwicklung der Trigonometrie veränderte sich langsam die Art, wie man Bewegungen der Himmelskörper untersuchte. Statt Bewegungsmuster nur passiv zu beobachten und aufzuzeichnen, begannen Gelehrte, sie mathematisch zu modellieren, um zukünftige astronomische Ereignisse mit größerer Genauigkeit vorhersagen zu können. Die Trigonometrie wurde noch weit bis ins 16. Jahrhundert rein zur Unterstützung der Astronomie studiert, doch dann kamen in Europa neue Entwicklungen in Gang. De Triangulis Omnimodis (»Über Dreiecke aller Art«) wurde 1533 vom deutschen Mathematiker Johann Müller, genannt Regiomontanus, veröffentlicht. Ein Nachschlagwerk aller bekannten Sätze über Seiten und Winkel sowohl von ebenen Dreiecken als auch sphärischen Dreiecken, die auf einer Kugeloberfläche liegen. Ein Wendepunkt für die Trigonometrie: Sie war nun nicht mehr nur ein Teilgebiet der Astronomie, sondern ein wesentlicher Bestandteil der Geometrie.

»Eine Logarithmentafel ist eine kleine Tabelle, mit deren Hilfe wir Kenntnisse über alle geometrischen Dimensionen und Bewegungen im Raum erlangen können. «

John Napier Mirifici Logarithmorum Canonis Descriptio , 1614

Doch die Trigonometrie entwickelte sich noch weiter: Obwohl ihre natürliche Heimat die Geometrie ist, wandte man sie auch zunehmend in Algebra an. Der französische Mathematiker François Viète zeigte, wie man algebraische Gleichungen durch trigonometrische Winkelfunktionen in Verbindung mit dem neuen System imaginärer Zahlen (die der italienische Mathematiker Rafael Bombelli 1572 eingeführt hatte) lösen konnte.

Ende des 16. Jahrhunderts modellierte der italienische Physiker und Astronom Galileo Galilei mit der Trigonometrie Bahnen von Geschossen im Einfluss der Schwerkraft. Dieselben Gleichungen verwendet man auch heute noch, um Raketenbahnen vorauszuberechnen. Ebenfalls im 16. Jahrhundert bestimmte der niederländische Kartograf Gemma Frisius Entfernungen trigonometrisch, sodass man erstmals genau vermessene Karten erstellen konnte.

Die Entwicklung der Trigonometrie nahm im 17. Jahrhundert Fahrt auf. Die Entdeckung von Logarithmen durch den schottischen Mathematiker John Napier 1614 ermöglichte es, genaue Sinus-, Kosinus- und Tangenstabellen zu erstellen. 1722 ging der französische Mathematiker Abraham de Moivre einen Schritt weiter als Viète und zeigte, wie man die Winkelfunktionen in der Analysis komplexer Zahlen nutzen kann. Diese Zahlen haben eine reellen und einen imaginären Teil und spielten eine bedeutende Rolle im Fortschritt der Mechanik und Elektrotechnik. Leonhard Euler leitete aus Moivres Ergebnissen die »eleganteste Gleichung der Mathematik« her: e iπ + 1 = 0, auch »Eulers Identität« genannt.

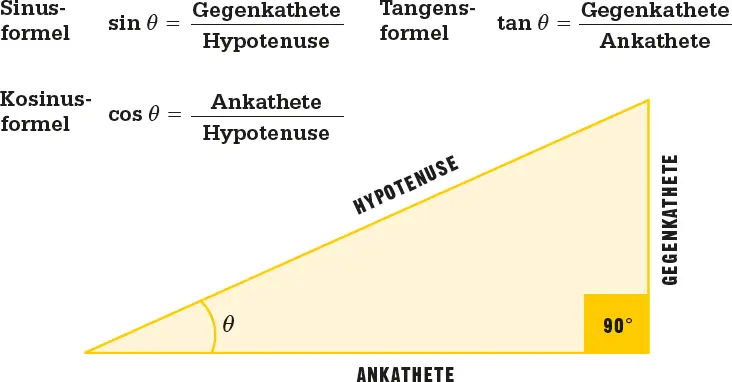
Um den unbekannten Winkel θ in einem rechtwinkligen Dreieck zu bestimmen, verwendet man die Sinusformel, wenn die Längen der Gegenkathete und der Hypotenuse bekannt sind, die Kosinusformel, wenn Ankathete und Hypotenuse bekannt sind, und die Tangensformel, wenn die beiden Katheten bekannt sind.

Triangulationspunktewie dieser Pfeiler in Wales wurden in vielen Ländern zur systematischen Vermessung aufgebaut, in Großbritannien vom Ordnance Survey ab 1936.

Im 18. Jahrhundert analysierte Joseph Fourier Schwingungen und Wellen mithilfe von Winkelfunktionen. Diese »Fourierreihen« sind seither in vielen Wissenschaftsgebieten wie Optik oder Elektromagnetismus und, in jüngerer Zeit, in der Quantenmechanik sehr wichtig.

Seit die Babylonier und Ägypter über die Länge des Schattens eines in den Boden gesteckten Stabs nachdachten, über Architektur und Astronomie bis hin zu modernen Anwendungen: Die Trigonometrie gehört fest zur mathematischen Sprache, mit der wir das Universum erklären.

Hipparchos

Hipparchos wurde um 190 v. Chr. in Nicäa, dem heutigen Iznik (Türkei), geboren. Wenig ist über sein Leben bekannt. Ruhm erlangten seine astronomischen Studien, die er auf der griechischen Insel Rhodos durchführte. Seine Arbeit wurde im Almagest von Ptolemäus verewigt, der ihn als »Wahrheitsliebenden« bezeichnete.

Das einzige erhaltene Werk von ihm ist seine Kommentarsammlung zu den Phainomena des Dichters Aratos und des Mathematikers und Astronomen Eudoxos, deren Beschreibung der Sternbilder er als ungenau kritisierte. Hipparchos’ wichtigstes Werk war Über Größen und Abstände (heute verloren, aber von Ptolemäus verwendet) über die Bahn von Sonne und Mond, mit denen er Sonnenwenden und Tagundnachtgleichen berechnen konnte. Er erstellte auch einen Sternenkatalog, den Ptolemäus wohl in den Almagest integrierte. Hipparch starb 120 v. Chr.

Hauptwerk

2. Jh. v. Chr. Peri Megethon kai Apostematon (Über Größen und Abstände)

IM KONTEXT

SCHLÜSSELZIVILISATION

Altes China(um 1700 v. Chr. – 600 n. Chr.)

TEILGEBIET

Zahlensysteme

FRÜHER

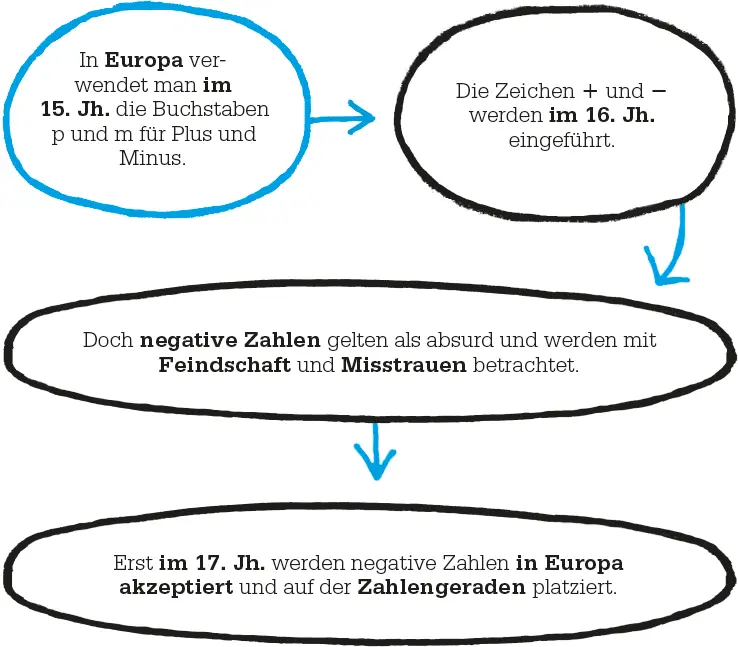
um 1000 v. Chr.In China verwendet man erstmals Bambusstäbe zur Darstellung von Zahlen, darunter auch negative Zahlen.

SPÄTER

628 n. Chr.Der indische Mathematiker Brahmagupta stellt Regeln zum Rechnen mit negativen Zahlen auf.

1631In Artis Analyticae Praxis , das 10 Jahre nach seinem Tod veröffentlicht wird, akzeptiert der Brite Thomas Harriot negative Zahlen in algebraischen Darstellungen.

Während das Konzept negativer Größen in der Praxis schon im Altertum, besonders in China, verwendet wurde, wurden negative Zahlen in der Mathematik erst sehr viel später zugelassen. Denker der griechischen Antike und viele spätere europäische Mathematiker hielten negative Zahlen – und die Vorstellung, dass etwas weniger als nichts ist – für absurd. Erst im 17. Jahrhundert begannen europäische Mathematiker, negative Zahlen völlig anzunehmen.