John Farndon - Big Ideas. Das Mathematik-Buch

Eratosthenes

Der um 276 v. Chr. in Kyrene, einer griechischen Stadt in Libyen, geborene Eratosthenes studierte in Athen und wurde Mathematiker, Astronom, Geograf, Musikologe, Literaturkritiker und Dichter. Er war der Chefbibliothekar der Bibliothek von Alexandria, der größten akademischen Institution der antiken Welt. Eratosthenes gilt als Vater der Geografie, da er sie als akademische Disziplin begründete und benannte und einen Großteil der geografischen Begriffe einführte, die auch heute noch benutzt werden.

Er erkannte auch, dass die Erde kugelförmig ist, und berechnete ihren Umfang, indem er den Höhenwinkel der Sonne zu Mittag in Assuan in Südägypten und Alexandria im Norden des Landes verglich. Zudem erstellte er die erste Weltkarte, die Meridiane, den Äquator und sogar die Polargebiete zeigte. Er starb um 194 v. Chr.

Hauptwerke

Mensuram orae ad terram (»Über die Messung der Erde«)

Geographika (»Geografie«)

IM KONTEXT

SCHLÜSSELFIGUR

Apollonios von Perge(um 262–190 v. Chr.)

TEILGEBIET

Geometrie

FRÜHER

um 300 v. Chr.Euklids Elemente bildet die axiomatische Basis der ebenen Geometrie.

um 250 v. Chr.In Peri Konoeideon kai Sphairoeideon (Über Konoide und Sphäroide) behandelt Archimedes Körper, die bei der Rotation von Kegelschnitten entstehen.

SPÄTER

um 1079 n. Chr.Der Perser Omar Chayyam löst algebraische Gleichungen geometrisch mit Kegelschnitten.

1639Der 16-jährige Pascal behauptet: Geradenschnittpunkte gegenüberliegender Punkte eines nicht ausgearteten Kegelschnittsechsecks liegen auf einer Geraden.

Unter den vielen mathematischen Pionieren der griechischen Antike war Apollonios von Perge einer der brillantesten. Er studierte Mathematik, als Euklids großes Werk Elemente bereits im Umlauf war, und wandte die euklidische Methode an, von »Axiomen« (als wahr akzeptierte Aussagen) als Startpunkt für Ableitungen und Beweise auszugehen.

Apollonios schrieb über viele Themen, darunter Optik (wie sich Lichtstrahlen ausbreiten) und Astronomie ebenso wie Geometrie. Viele seiner Werke sind nur in Fragmenten erhalten, doch das einflussreichste, Konika (»Kegelschnitte«), kennen wir fast vollständig. Es hatte acht Bände, von denen sieben erhalten sind: Bücher 1–4 in Griechisch und Bücher 5–7 in Arabisch. Sie waren für Mathematiker geschrieben, die mit der Geometrie bereits gut vertraut waren.

»Ich habe meinen Sohn zu dir gesandt mit dem zweiten Buch meiner gesammelten Konika . Lies es sorgfältig und teile es mit denjenigen, die es wert sind, an solchen Studien teilzunehmen. «

Apollonios von PergeEinleitung zu Buch 2 der Konika

Frühe griechische Mathematiker wie Euklid konzentrierten sich auf Geraden und Kreise als die reinsten geometrischen Formen. Apollonios dachte dreidimensional: Kombiniert man einen Kreis mit allen Geraden (»Mantellinien«), die von ihm ausgehen und sich in einem Punkt (»Spitze«) über oder unter der Kreisebene treffen, dann entsteht ein Kegel oder Konus. Wenn man den Kegel mit einer Ebene schneidet, erhält man verschiedene Kurven, die man Kegelschnitte nennt.

In Konika legte Apollonios diese neue Welt mathematischer Konstruktionen detailliert dar und studierte die Eigenschaften von Kegelschnitten. Dabei ging er von Doppelkegeln (zwei Kegel, die sich an der Spitze berühren) mit potenziell unendlich weit entfernten Grundflächen aus. Drei der Kurven nannte er Ellipse, Parabel und Hyperbel. Eine Ellipse entsteht, wenn die Ebene den Kegel schief schneidet. Eine Parabel entsteht, wenn die Ebene parallel zu einer der Mantellinien des Kegels ist, und eine Hyperbel, wenn die Ebene senkrecht (parallel zur Kegelachse) ist. Er sah den Kreis als separate Form, aber er ist eigentlich eine Art Ellipse die aus einer Schnittebene senkrecht zur Achse resultiert.

Zur Beschreibung dieser Objekte verwendetet Apollonios keine Zahlen oder Gleichungen. Doch sein Zugang mit Geraden, die von einem Punkt ausgehen, nahm die spätere Idee von Koordinatensystemen voraus. Er entwickelte dies nicht so detailliert wie 1800 Jahre später die Franzosen René Descartes und Pierre de Fermat, kam aber Koordinatendarstellungen von Kegelschnitten nahe. Einige Dinge hielten Apollonios zurück: Er verwendete keine negativen Zahlen und arbeitete nicht explizit mit der Null. Während das von Descartes entwickelte kartesische Koordinatensystem vier Quadranten der Ebene (mit positiven und negativen Koordinaten) abdeckt, arbeitete Apollonios nur in einem.

»[Kegelschnitte sind] der notwendige Schlüssel, mit dem man das Wissen über die wichtigsten Gesetze der Natur erlangen kann. «

Alfred North WhiteheadBritischer Mathematiker An Introduction to Mathematics , 1911

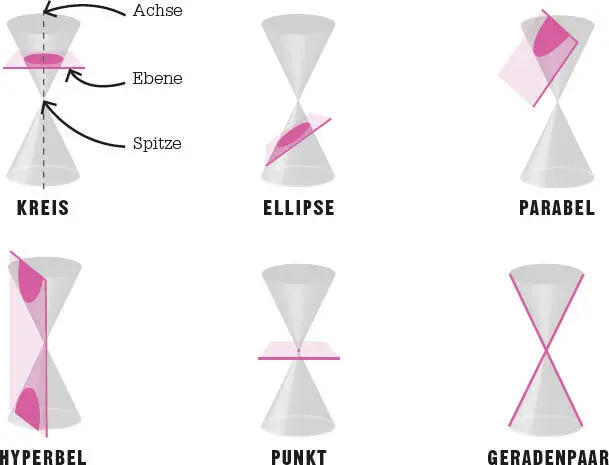
Schneidet eine Ebene einen (Doppel-)Kegel,entsteht ein Kegelschnitt. Neben den von Apollonios beschriebenen Kurven kann dies, wenn die Ebene durch die Kegelspitze geht, je nach Winkel ein Punkt, eine Gerade oder ein Geradenpaar sein.

Apollonios’ Werke regten viele Fortschritte an, die im Mittelalter in der islamischen Welt gemacht wurden. Während der Renaissance in Europa inspirierten sie Mathematiker, die analytische Geometrie zu entwickeln, eine Triebkraft der wissenschaftlichen Revolution.

Apollonios von Perge

Über das Leben von Apollonios wissen wir wenig. Er wurde um 262 v. Chr. in Perge in Südanatolien (heutige Türkei) geboren, das für die Verehrung der Göttin Artemis bekannt war. Er studierte jedoch bei euklidischen Gelehrten in Alexandria in Ägypten, dem Zentrum der antiken Wissenschaft.

Vermutlich schrieb Apollonios alle acht Bände der Konika (»Kegelschnitte«) in Ägypten. Die ersten Bände enthalten wenig, was nicht auch schon Euklid wusste, aber die späteren Bände stellen erhebliche Fortschritte in der Geometrie dar.

Neben den Arbeiten über Kegelschnitte soll Apollonios den Wert von Pi genauer angenähert haben als sein Zeitgenosse Archimedes und als Erster erkannt haben, dass ein sphärischer Spiegel die Sonnenstrahlen nur unvollkommen bündelt, ein Parabolspiegel dagegen gut.

Hauptwerk

um 200 v. Chr. Konika

IM KONTEXT

SCHLÜSSELFIGUR

Hipparchos von Nicäa(um 190–120 v. Chr.)