John Farndon - Big Ideas. Das Mathematik-Buch

TEILGEBIET

Geometrie

FRÜHER

um 1800 v. Chr.Die babylonische Tontafel Plimpton 322 listet pythagoreische Tripel, lange bevor Pythagoras den Satz a 2+ b 2= c 2aufstellt.

um 1650 v. Chr.Der ägyptische Papyrus Rhind zeigt, wie man die Steigung der Seiten einer Pyramide berechnet.

6. Jh. v. Chr.Pythagoras entdeckt seinen Satz über die Seitenlängen von Dreiecken.

SPÄTER

500 n. Chr.Die Inder nutzen trigonometrische Tabellen.

1000 n. Chr.Islamische Gelehrte rechnen mit Dreiecken verschiedener Seiten- und Winkelverhältnisse.

Trigonometrie, nach den griechischen Wörtern trigonon (»Dreieck«) und metron (»Maß«), ist enorm wichtig sowohl für die historische Entwicklung der Mathematik als auch für moderne Anwendungen. Sie ist wohl eine der nützlichsten mathematischen Disziplinen, denn sie ermöglicht uns, in der Welt zu navigieren, Elektrizität zu verstehen und die Höhe von Bergen zu vermessen.

Seit der Antike haben Zivilisationen rechte Winkel in der Architektur geschätzt. Dies führte Mathematiker zum Studium rechtwinkliger Dreiecke: Alle Dreiecke haben drei Winkel, und bei rechtwinkligen Dreiecken ist einer ein rechter Winkel (90 °). Die beiden kürzeren Seiten, die am rechten Winkel anliegen, heißen Katheten. Sie sind nicht unbedingt gleich lang. Die längste Seite gegenüber dem rechten Winkel nennt sich Hypotenuse.

Im frühen 20. Jahrhundert wurde eine babylonischen Tontafel von etwa 1800 v. Chr. mit Informationen über Dreiecke entdeckt. Auf der Tafel, die 1923 von dem US-Verleger George Plimpton gekauft wurde und die man Plimpton 322 nennt, waren numerische Daten über rechtwinklige Dreiecke eingeritzt. Ihre genaue Bedeutung ist umstritten, doch sie listet anscheinend pythagoreische Tripel (je drei ganze Zahlen – Seitenlängen eines rechtwinkligen Dreiecks) neben anderen Zahlengruppen, die den Quadraten der Seiten ähneln, auf. Der ursprüngliche Zweck der Tafel ist unbekannt. Sie war vielleicht ein praktisches Nachschlagewerk für Vermessungen.

»Auch wenn er sie nicht erfand, ist Hipparchos der erste, für dessen systematische Verwendung der Trigonometrie wir schriftliche Belege haben. «

Sir Thomas HeathBritischer Mathematikhistoriker A History Of Greek Mathematics , 1921

Etwa gleichzeitig mit den Babyloniern entwickelten die Ägypter ein Interesse an der Geometrie. Die Triebkräfte dafür waren nicht nur Monumentalbauten, sondern auch die jährlichen Überschwemmungen des Nils, nach denen man die Felder immer wieder neu vermessen musste. Das mathematische Interesse der Ägypter ist klar im Papyrus Rhind dokumentiert, eine Schriftrolle mit einer Anzahl von Aufgaben, u. a. über Bruchrechnung. Eine lautet: »Berechnung einer Pyramide: 360 meh (Ellen) ist die Seite der Grundfläche, 250 meh ist die Höhe. Lass mich ihren seqed wissen.« Ein seqed ist ein Maß für Steigungen, es geht also um ein rein trigonometrisches Problem.

Beeinflusst von den babylonischen Überlegungen entwickelten die Griechen die Trigonometrie als Teilgebiet der Mathematik mit allgemeingültigen Regeln und nicht nur Zahlentabellen wie ihre Vorgänger. Im 2. Jahrhundert v. Chr. interessierte sich der Astronom und Mathematiker Hipparchos, der als Begründer der Trigonometrie gilt, besonders für Dreiecke, die Kreisen und Kugeln einbeschrieben waren. Und ebenso für die Beziehungen zwischen Winkeln und Längen von Sehnen (Strecken zwischen Punkten auf einem Kreis oder Kurve). Hipparchos erstellte Tabellen, die letztlich die ersten echten Tafeln trigonometrischer Werte waren.

Etwa 300 Jahre später schrieb der griechisch-römische Universalgelehrte Klaudios Ptolemaios (lat: Claudius Ptolemaeus) das Werk Mathematike Syntaxis oder Megiste Syntaxis (»Mathematische Zusammenstellung« bzw. »Größte Zusammenstellung«), das später als al-Magisti ins Arabische und von dort als Almagest ins Lateinische übersetzt wurde. Darin führte er die Arbeiten von Hipparchos über Dreiecke und Kreissehnen fort und leitete Formeln ab, um die Positionen von Himmelskörpern zu berechnen, deren Bahnen er als Kreise um die Erde annahm. Ptolemäus verwendete wie seine Vorgänger das babylonische Sexagesimalsystem, ein Stellenwertsystem zur Basis 60.

Im Mittelalterverwendete man Astrolabien, die auf trigonometrischen Prinzipien beruhten, um Positionen von Himmelskörpern zu bestimmen. Hipparch soll sie erfunden haben.

Ptolemäus’ Arbeiten wurden in Indien fortgeführt, wo das wachsende Gebiet der Trigonometrie zur Astronomie zählte. Der Mathematiker Aryabhata (474–550 n. Chr.) studierte Sehnen und berechnete die erste Wertetabelle einer Funktion, die wir heute Sinusfunktion nennen: Eine Winkelfunktion des rechtwinkligen Dreiecks, die gleich dem Verhältnis von Gegenkathete (dem Winkel gegenüberliegender Seite) und Hypotenuse (längster Seite) ist (siehe Grafik).

Arten der Trigonometrie

a = Gegenkathete

b = Ankathete

c = Hypotenuse

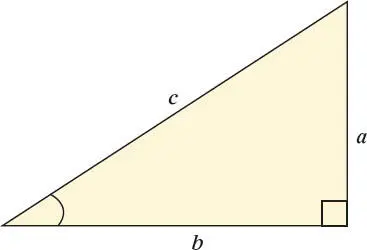
Ebene Trigonometriebeschäftigt sich mit Dreiecken in der Ebene (einer flachen, zweidimensionalen Fläche). Mit ihr berechnen etwa Architekten die Stabilität von Gebäuden oder Physiker die Bewegung von Körpern.

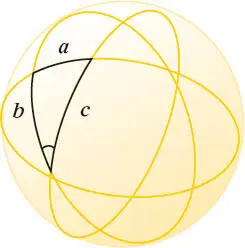
Sphärische Trigonometriebehandelt Dreiecke auf Kugeloberflächen (dreidimensional gekrümmte Flächen). Damit berechnen Astronomen Positionen von Himmelskörpern und Navigatoren Längen- und Breitengrade.

Im 7. Jahrhundert lieferte ein anderer großer indischer Mathematiker und Astronom, Brahmagupta, eigene Beiträge zur Geometrie und Trigonometrie, darunter den heute »Formel von Brahmagupta« genannten Satz. Damit findet man die Fläche von Sehnenvierecken, also Vierecken, die einem Kreis einbeschrieben sind. Ihre Fläche lässt sich auch durch trigonometrische Verfahren berechnen, wenn man das Viereck in zwei Dreiecke teilt.

»Die Trigonometrie, wie jeder andere Zweig der Mathematik, ist nicht das Werk eines einzelnen Menschen oder einer einzelnen Nation. «

Carl Benjamin BoyerUS-Mathematikhistoriker A History of Mathematics , 1968

Schon Brahmagupta hatte Tafeln mit Sinuswerten erstellt, und im 9. Jahrhundert berechnete der persische Astronom und Mathematiker Habasch al-Hasib (»Habasch der Rechner«) Sinus-, Kosinus- und Tangenstabellen für die Berechnung von Seiten und Winkeln in Dreiecken. Etwa zur gleichen Zeit entwickelte al-Battani (lat.: Albatenius) die Arbeiten von Ptolemäus über die Sinusfunktion weiter und wandte sie auf astronomische Berechnungen an. Er machte höchst genaue Beobachtungen von Himmelskörpern in ar-Raqqa (heutiges Syrien). Der Grund, warum islamische Gelehrte Trigonometrie weiterentwickelten, war nicht nur astronomische Neugier, sondern auch praktisch motiviert, denn Moslems müssen die Richtung zur Heiligen Stadt Mekka an jedem Ort der Erde bestimmen können.