John Farndon - Big Ideas. Das Mathematik-Buch

Einige Forscher meinen, die Rechentafel sei tatsächlich babylonischen Ursprungs. Das Wort abax könnte vom phönizischen oder hebräischen Wort »Staub« ( abag ) kommen und sich auf viel ältere Systeme beziehen, bei denen Zählsteine auf ein in den Sand gezeichnetes Gitter gelegt wurden. Das babylonische Stellenwertsystem, das um 2000 v. Chr. entstand, könnte davon angeregt worden sein.

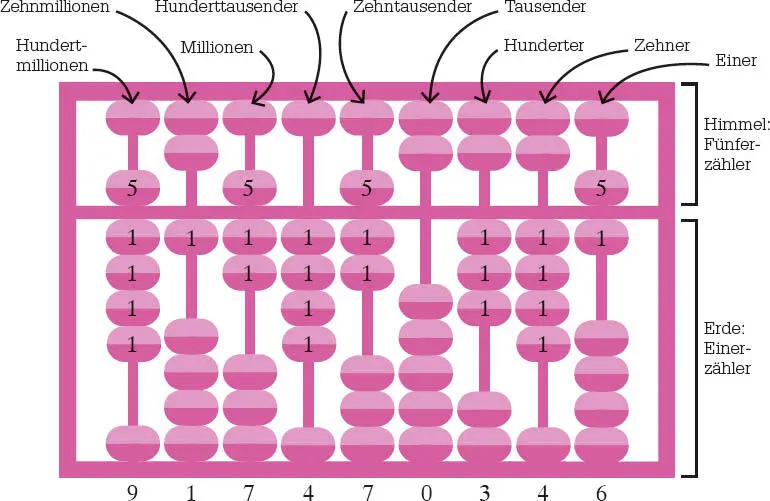
Der Suanpan ist auf die Zahl 917 470 346 eingestellt. Er ist traditionell ein 2:5-Abakus: Jede Spalte hat zwei »Himmelskugeln«, jeweils mit dem Wert 5 und fünf »Erdkugeln« je mit einem Wert 1. So kann man in einer Spalte Werte von 0–15 darstellen. Damit sind Berechnungen im chinesischen Zahlensystem mit der Basis 16 möglich, bei der jede Stelle 16 statt 10 Ziffern in unserem Dezimalsystem annehmen kann. Zur Addition stellt man die erste Zahl ein und verschiebt von rechts nach links jeweils entsprechend viele Kugeln. Ebenso geht man bei der Subtraktion vor. Der Übertrag wird zur nächsten Spalte gerechnet oder auch beim Subtrahieren »geborgt«, ähnlich dem handschriftlichen Rechnen.

Die Römer verbesserten das Rechenbrett zu einem Gerät, mit dem man erheblich einfacher rechnen konnte. Statt der horizontalen Linien hatte der römische Abacus vertikale Schlitze, in denen kleine Steinchen – oder, auf Latein, calculi – verschoben wurden. Daher stammt unser Wort »Kalkulation«.

Eine Art Abakus hatten auch die präkolumbianischen Kulturen Mittelamerikas. Er basierte auf dem Vigesimalsystem, einem Stellenwertsystem zur Basis 20, und nutzte auf Schnüren aufgefädelte Maiskörner, um mit bis zu fünfstelligen Zahlen zu rechnen. Es sind keine Exemplare erhalten, doch er wurde wohl vor 3000 Jahren von den Olmeken erfunden. Um 1000 n. Chr. kannten ihn die Azteken als Nepohualtzintzin (»persönlicher Kontenzähler«) und trugen ihn als Armband.

Etwa im 2. Jahrhundert n. Chr. waren Abaki in China ein gängiges Hilfsmittel. Der chinesische Abakus oder Suanpan ähnelte dem römischen, doch statt Steinchen im Metallrahmen hatte er hölzerne Kugeln auf Stäben – Vorbild heutiger Abaki. Ob der römische oder chinesische Abakus früher entstand, ist unklar. Ihre Ähnlichkeiten dürften Zufall sein und darauf zurückgehen, wie Menschen mit fünf Fingern zählten. Beide Abaki haben zwei Bereiche: der untere zählt Einer und der obere Fünfer.

Im 2. Jahrtausend n. Chr. war der Suanpan in ganz Asien verbreitet. In Japan wurde er im 14. Jahrhundert eingeführt und Soroban genannt. Im 20. Jahrhundert hatte sich der Soroban zu einem 1:4-Abakus weiterentwickelt (also einer oberen Zählkugel und vier unteren Zählkugeln je Stab).

Die weibliche Personifikationder Arithmetik beurteilt einen Wettbewerb zwischen dem Römer Boethius, der schriftlich rechnet, und dem Griechen Pythagoras mit einem Rechenbrett.

Das Soroban-Turnier

Japanische Schüler lernen immer noch den Soroban (japanischen Abakus) zur Entwicklung des Kopfrechnens. Der Soroban wird auch für komplizierte Berechnungen genutzt. Soroban -Experten können viele Berechnungen oft schneller durchführen als jemand, der sie in einen Taschenrechner eintippt.

Jedes Jahr nehmen die besten Abakusmeister ganz Japans am Soroban -Turnier teil. In einem Ausscheideverfahren konkurrieren sie miteinander und müssen Schnelligkeit und Genauigkeit beweisen. Einer der Höhepunkte des Turniers ist Flash Anzan ™, ein Wettbewerb im Kopfrechnen, bei dem die Teilnehmer einen Abakus visualisieren und dadurch 15 dreistellige Zahlen addieren – ohne physisches Exemplar. Die Zahlen werden auf einem großen Bildschirm immer schneller gezeigt. 2017 lag der Weltrekord im Flash Anzan bei der Addition von 15 Zahlen in 1,68 Sekunden.

IM KONTEXT

SCHLÜSSELFIGUR

Archimedes(etwa 287–212 v. Chr.)

TEILGEBIET

Zahlentheorie

FRÜHER

um 1650 v. Chr.Der Papyrus Rhind , ein Mathematikübungsbuch eines ägyptischen Schreibers aus dem Mittleren Reich, enthält Näherungswerte für π .

SPÄTER

5. Jh. n. Chr.Der Chinese Zu Chongzhi berechnet π auf sieben Dezimalstellen genau.

1671Der schottische Mathematiker James Gregory entwickelt die Arcustangensmethode zur Berechnung von π . Der Deutsche Gottfried Leibniz macht drei Jahre später die gleiche Entdeckung.

2019In Japan berechnet Emma Haruka Iwao mithilfe eines Cloud-Rechendienstes π auf mehr als 31 Billionen Nachkommastellen genau.

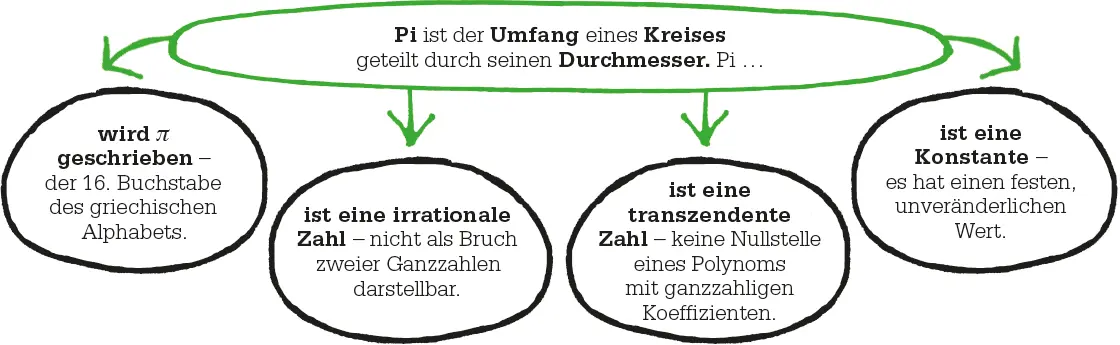
Dass die Kreiszahl Pi ( π ) – das Verhältnis von Umfang zu Durchmesser eines Kreises – mit dem ungefähren Wert 3,1415 nicht genau dargestellt werden kann, egal wie viele Dezimalstellen man ausschreibt, hat Gelehrte seit Jahrhunderten fasziniert. Der walisische Mathematiker William Jones verwendete 1706 als Erster den griechischen Buchstaben π (Pi) als Symbol für die Zahl, doch ihre Bedeutung für die Berechnung von Umfang und Fläche von Kreisen bzw. dem Volumen von Kugeln ist seit Jahrtausenden bekannt.

Möglichst exakte Werte von Pi sind nicht einfach zu bestimmen und man sucht immer noch nach weiteren Dezimalstellen. Zwei der ältesten Näherungswerte für π stehen in altägyptischen Texten, dem Papyrus Rhind und dem Papyrus Moskau 4676 . Der Papyrus Rhind , wohl ein Übungstext für angehende Schreiber, erklärt etwa die Berechnung des Volumens von Zylindern und der Fläche von Kreisen. Um die Kreisfläche zu berechnen, sollte man die Fläche eines Quadrats berechnen, dessen Seitenlänge 8/ 9des Kreisdurchmessers beträgt. Dies impliziert einen Wert für π von (auf vier Stellen genau berechnet) etwa 3,1605, also nur etwa 0,6 % größer als der bisher genaueste bekannte Wert.

Die Kreiszahl Pi ist nicht nur in der Geometrie, sondern in der gesamten Mathematik allgegenwärtig.

In Babylon bestimmte man die Fläche eines Kreises, indem man das Quadrat des Umfangs mit 1/ 12multiplizierte, was auf einen Wert für π von 3 deutet. Dieser Wert erscheint auch in der Bibel: »Und er machte das Meer [Bronzebecken], gegossen, von einem Rand zum andern zehn Ellen weit, ganz rund und fünf Ellen hoch, und eine Schnur von dreißig Ellen war das Maß ringsherum« (1. Könige 7:23).

250 v. Chr. entwickelte der Grieche Archimedes einen Algorithmus zur Bestimmung des Werts von π , indem er reguläre Polygone (Vielecke) konstruierte, die einem Kreis eingeschrieben und umschrieben waren. Da sie größer bzw. kleiner als der Kreis sind, ergeben ihre Umfänge obere und untere Grenzen für den Kreisumfang. Mit dem Satz von Pythagoras – in einem rechtwinkligen Dreieck ist das Quadrat der Hypotenuse (Seite gegenüber dem rechten Winkel) gleich der Summe der Quadrate der Katheten (der anderen beiden Seiten) – fand Archimedes die Beziehung zwischen den Seitenlängen, wenn die Zahl der Seiten verdoppelt wurde. So konnte er Vielecke mit bis zu 96 Seiten verwenden. Die Idee, Kreisflächen durch Polygone anzunähern, wurde schon über 200 Jahre vor Archimedes vorgeschlagen, aber er betrachtete als Erster sowohl eingeschriebene als auch umschriebene Polygone.