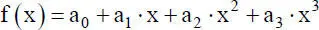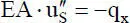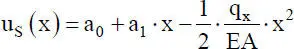(2.13a) 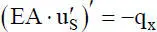
(2.13b) 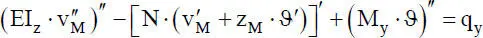
(2.13c) 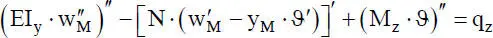
(2.13d) 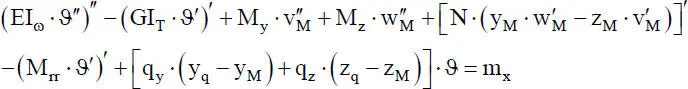
Mrr: siehe Tabelle 4.1
Die DGLn (2.13)zeigen, wie die bei der linearen Stabtheorie voneinander unabhängigen vier Teilprobleme „Normalkraft, Biegung um die y- bzw. z-Achse und Torsion“ bei Theorie II. Ordnung miteinander verknüpft sind. Die Kopplung wird durch die Schnittgrößen verursacht und führt dazu, dass das Differentialgleichungssystem (2.13)analytisch nicht gelöst werden kann. Für gewisse Sonderfälle sind Lösungen bekannt, wobei vornehmlich die Problemstellung „Biegeknicken“ von allgemeiner Bedeutung ist. In den DGLn (2.13)ist die Normalkraft N als Zugkraft positiv definiert und die Gleichstreckenlast q xgreift im Schwerpunkt an, s. auch Bild 1.9.
Aus Gl. (2.13c)folgt für ϑ(x) = 0 sowie konstante Steifigkeit EI yund Drucknormalkraft ND die bekannte DGL für das Biegeknicken um die starke Achse:
(2.14) 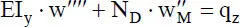
Für die Lösung der DGLn ist es zweckmäßig, Stababschnitte der Länge ℓ zu betrachten und als Parameter Stabkennzahlen ε einzuführen. Damit kann wie folgt formuliert werden:
(2.15) 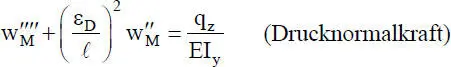
(2.16) 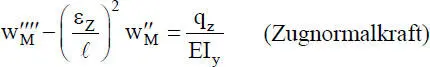
(2.17) 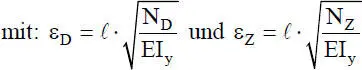
Die Lösungen der DGLn (2.15)und (2.16)werden in Abschnitt 2.5angegeben, da sie dort zur Beurteilung der Ansatzfunktionen für die Verformungen benötigt werden.
Abschließend soll in diesem Abschnitt noch das Stabilitätsproblem Plattenbeulenangesprochen werden. Nach [26] lautet die homogene DGL:
(2.18) 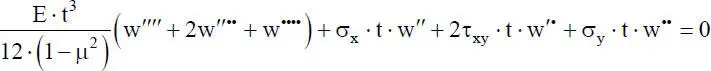
In Gl. (2.18)bedeuten die hochgestellten Striche Ableitungen nach x und die hochge-stellten Punkte Ableitungen nach y. Die Spannungen σ xund σ ysind als Druckspannungenpositiv definiert, was der Vorgehensweise beim Biegeknicken für Drucknormalkräfte entspricht. Wenn man in Gl. (2.18)σ y= τ = 0 setzt, so ergibt sich eine homogene DGL, die mit der DGL für das Biegeknicken von Stäben formal übereinstimmt:
(2.19) 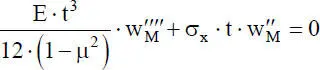
Aufgrund dieser Übereinstimmung ergeben sich für die homogenen DGLn (2.15)und (2.19)die gleichen Lösungsfunktionen.
2.5 Ansatzfunktionen für die Verformungen
2.5.1 Grundsätzliches
Ansatzfunktionen für die Beschreibung der Verformungen müssen geeignet sein, die bei einem Tragwerk möglichen Verformungen in zutreffender Weise zu erfassen. Fast ausschließlich werden als Funktionsverläufe Polynomfunktionenverwendet, die diese zentrale Forderung in vielen Anwendungsfällen exakt erfüllen. Bei einigen praxisrelevanten Aufgabenstellungen sind sie jedoch nur Näherungen und erfordern daher eine genügend feine FE-Modellierung, damit die Genauigkeit der Rechenergebnisse ausreichend ist. Beispiele dazu sind das Biegeknicken von Stäben und andere Fälle, die in Abschnitt 2.5.3angesprochen werden.
Ein weiterer wichtiger Punkt ist die Erfassung der Randbedingungen, wobei geometrische und physikalische Randbedingungen unterschieden werden. Die Ansatzfunktionen sollten zweckmäßigerweise so gewählt werden, dass die Verformungsgrößen in den Knoten unmittelbar die Berücksichtigung der geometrischen Randbedingungenermöglichen. Bei Biegung um die y-Achse bedeutet dies beispielsweise, dass die Verschiebung w Mund die Verdrehung 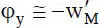 als Knotenfreiwerte in den Ansatzfunktionen enthalten sein sollten. Physikalische Randbedingungensind Bedingungen für die Schnittgrößen an den Rändern oder Enden von baustatischen Systemen. Als Beispiel zur Biegung soll hier die Randbedingung M y= 0 an einem Stabende betrachtet werden. Aus Tabelle 2.3liest man
als Knotenfreiwerte in den Ansatzfunktionen enthalten sein sollten. Physikalische Randbedingungensind Bedingungen für die Schnittgrößen an den Rändern oder Enden von baustatischen Systemen. Als Beispiel zur Biegung soll hier die Randbedingung M y= 0 an einem Stabende betrachtet werden. Aus Tabelle 2.3liest man 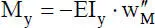 ab, so dass aus M y= 0 unmittelbar
ab, so dass aus M y= 0 unmittelbar 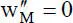 folgt. Man kann natürlich Krümmungen
folgt. Man kann natürlich Krümmungen 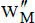 oder vergleichbare Größen, die zu physikalischen Randbedingungen bzw. entsprechenden Schnittgrößen korrespondieren, als Knotenfreiwerte in den Ansatzfunktionen berücksichtigen. Dies ist vereinzelt in FE-Programmen umgesetzt worden, hat sich aber nicht allgemein durchgesetzt, da damit gewisse Nachteile verbunden sind. Beim Weggrößenverfahren sollten daher in der Regel nur Knotenfreiwerte verwendet werden, die zu den geometrischen Randbedingungen korrespondieren.
oder vergleichbare Größen, die zu physikalischen Randbedingungen bzw. entsprechenden Schnittgrößen korrespondieren, als Knotenfreiwerte in den Ansatzfunktionen berücksichtigen. Dies ist vereinzelt in FE-Programmen umgesetzt worden, hat sich aber nicht allgemein durchgesetzt, da damit gewisse Nachteile verbunden sind. Beim Weggrößenverfahren sollten daher in der Regel nur Knotenfreiwerte verwendet werden, die zu den geometrischen Randbedingungen korrespondieren.
2.5.2 Polynomfunktionen für Stabelemente
Für finite Stabelemente sind Polynomfunktionen von zentraler Bedeutung. Als Beispiel wird die Funktion
(2.20) 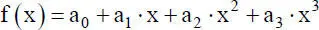
betrachtet. Diese viergliedrige Polynomfunktion hat den Polynomgrad 3 und Polynomkoeffizienten a 0, a 1, a 2und a 3. Verkürzt ausgedrückt spricht man auch von „Polynomen“.
Beanspruchung durch Normalkräfte
Die DGL für diesen Beanspruchungsfall kann Tabelle 2.3entnommen werden. Da später nur Stabelemente mit gleichbleibenden Querschnitten betrachtet werden, kann EA = konstant gesetzt werden und es ergibt sich die folgende DGL:
(2.21) 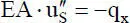
Die zweimalige Integration dieser DGL liefert:
(2.22) 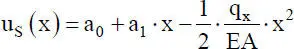
Читать дальше

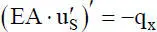
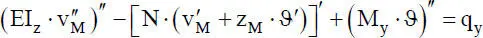
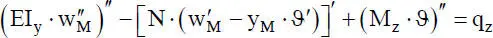
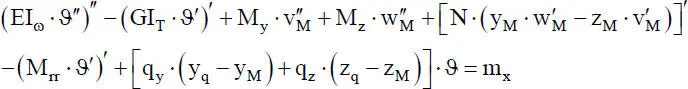
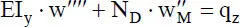
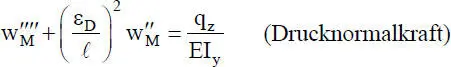
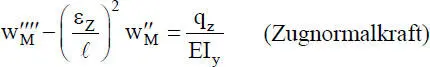
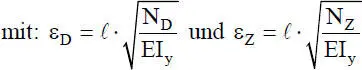
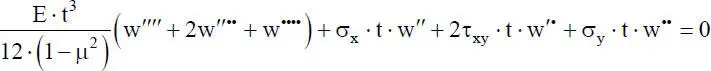
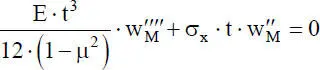
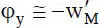 als Knotenfreiwerte in den Ansatzfunktionen enthalten sein sollten. Physikalische Randbedingungensind Bedingungen für die Schnittgrößen an den Rändern oder Enden von baustatischen Systemen. Als Beispiel zur Biegung soll hier die Randbedingung M y= 0 an einem Stabende betrachtet werden. Aus Tabelle 2.3liest man
als Knotenfreiwerte in den Ansatzfunktionen enthalten sein sollten. Physikalische Randbedingungensind Bedingungen für die Schnittgrößen an den Rändern oder Enden von baustatischen Systemen. Als Beispiel zur Biegung soll hier die Randbedingung M y= 0 an einem Stabende betrachtet werden. Aus Tabelle 2.3liest man 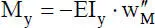 ab, so dass aus M y= 0 unmittelbar
ab, so dass aus M y= 0 unmittelbar 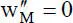 folgt. Man kann natürlich Krümmungen
folgt. Man kann natürlich Krümmungen 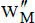 oder vergleichbare Größen, die zu physikalischen Randbedingungen bzw. entsprechenden Schnittgrößen korrespondieren, als Knotenfreiwerte in den Ansatzfunktionen berücksichtigen. Dies ist vereinzelt in FE-Programmen umgesetzt worden, hat sich aber nicht allgemein durchgesetzt, da damit gewisse Nachteile verbunden sind. Beim Weggrößenverfahren sollten daher in der Regel nur Knotenfreiwerte verwendet werden, die zu den geometrischen Randbedingungen korrespondieren.
oder vergleichbare Größen, die zu physikalischen Randbedingungen bzw. entsprechenden Schnittgrößen korrespondieren, als Knotenfreiwerte in den Ansatzfunktionen berücksichtigen. Dies ist vereinzelt in FE-Programmen umgesetzt worden, hat sich aber nicht allgemein durchgesetzt, da damit gewisse Nachteile verbunden sind. Beim Weggrößenverfahren sollten daher in der Regel nur Knotenfreiwerte verwendet werden, die zu den geometrischen Randbedingungen korrespondieren.