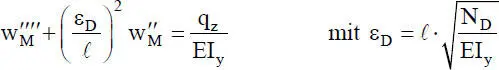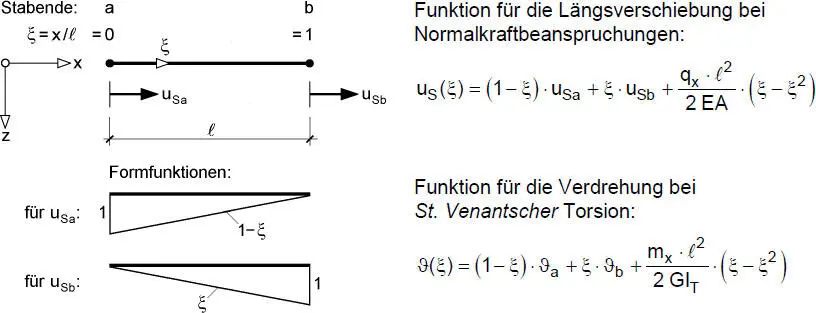
Bild 2.11 Stabelement und Funktionen für die Längsverschiebung bei Normalkraftbe-anspruchungen und die Verdrehung bei St. Venantscher Torsion
Wenn man den Fall q x= 0 betrachtet, ist die genaue Lösung ein Polynom 1. Grades mit einem linear veränderlichen Verlauf von uS(x). Die Integrationskonstanten a 0und a 1können mithilfe von Bild 2.11durch die Längsverschiebungen an den Enden des Stabelementes ersetzt werden. Mit den Randbedingungen u S(x = 0) = u Saund u S(x = ℓ ) = u Sbergeben sich die Integrationskonstanten zu:
(2.23) 
(2.24) 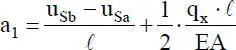
Wenn man nun die dimensionslose Koordinate ξ = x/ ℓ einführt, erhält man die folgende Funktion für die Längsverschiebungen:
(2.25) 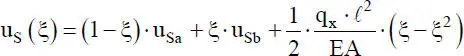
Da hier nur die Verschiebungen in den Knoten berücksichtigt werden (keine Ableitungen!), entsprechen die Formfunktionen in Bild 2.11den Koeffizientenfunktionen des Lagrangeschen Interpolationspolynoms für zwei Stützwerte. Formfunktionen werden bei der FEM häufig verwendet. Sie haben korrespondierend zu einerVerformungsgröße den Wert eins, während sich alle anderen Verformungsgrößen, mit denen die Verschiebungsfunktion beschrieben wird, zu null ergeben.
St. Venantsche Torsion
Bei wölbfreien Querschnitten ist der Wölbwiderstand I ω= 0, so dass reine St. Venantsche Torsion auftritt. Für diesen Sonderfall ergibt sich die DGL nach Tabelle 2.3unter der Annahme GI T= konst. zu:
(2.26) 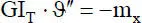
Ein Vergleich mit Gl. (2.21), d. h. mit der DGL für die Längsverschiebung, zeigt die formale Übereinstimmung der beiden Gleichungen. Man erhält daher für die Verdrehungen bei St. Venantscher Torsion den folgenden Funktionsverlauf im Stabelement (s. auch Bild 2.11):
(2.27) 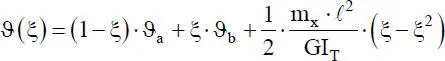
Biegung um die z-Achse
Wenn man gleichbleibende Querschnitte in den Stabelementen annimmt, ist EI z= konst. und man erhält mithilfe von Tabelle 2.3folgende Differentialgleichung:
(2.28) 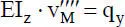
Die viermalige Integration dieser DGL liefert:
(2.29) 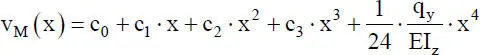
Es ergibt sich also ein Polynom 3. Grades mit den vier Integrationskonstanten c 0bis c 3, wenn man den Fall q y= 0 betrachtet. Wie bei der „Beanspruchung durch Normalkräfte“ werden die Integrationskonstanten durch ingenieurmäßig anschauliche Verformungsgrößen ersetzt. Mechanisch sinnvoll ist es die Durchbiegungen und Verdrehungenan den Elementenden als Freiwerte zu wählen, da die Durchbiegungen über die Elementgrenzen hinweg stetig, d. h. ohne Knicke, durchgehen müssen. Wie in Bild 2.12dargestellt lauten die gewählten Knotenfreiwerte: 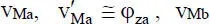 und
und 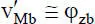 . Unter Verwendung der Randbedingungen
. Unter Verwendung der Randbedingungen 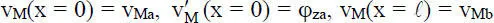 , und
, und 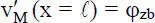 können die Integrationskonstanten in Gl. (2.29)ersetzt werden. Mit der dimensionslosen Koordinate ξ = x/ ℓ erhält man die folgende Funktion für die Durchbiegungdes Stabelementes in y-Richtung:
können die Integrationskonstanten in Gl. (2.29)ersetzt werden. Mit der dimensionslosen Koordinate ξ = x/ ℓ erhält man die folgende Funktion für die Durchbiegungdes Stabelementes in y-Richtung:
(2.30) 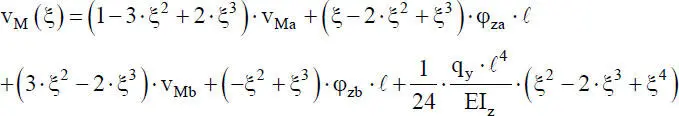
Gl. (2.30)ist ein Hermitesches Interpolationspolynom der Ordnung 2α = 4, da neben den Verschiebungen in den Punkten a und b auch die erste Ableitung zur Beschreibung der Durchbiegung verwendet wird.
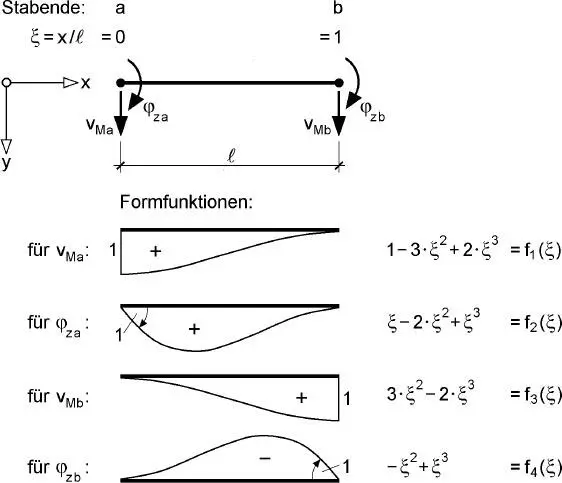
Bild 2.12 Stabelement und Formfunktionen f(ξ) für die Durchbiegung v M(ξ)
Biegung um die y-Achse
Wie Tabelle 2.3zeigt, ist dieser Beanspruchungsfall unmittelbar mit der Biegung um die z-Achse vergleichbar. Bei analoger Vorgehensweise erhält man die folgende Funktion für die Durchbiegungen wM(ξ)des Stabelementes in z-Richtung:
(2.31) 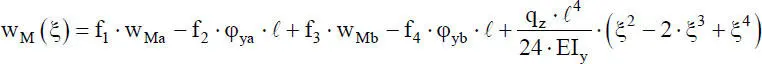
Die Formfunktionen f 1bis f 4können Bild 2.12entnommen werden, da sie für die Durchbiegung w M(ξ) und v M(ξ) identisch sind. Die negativen Vorzeichen in Gl. (2.31)ergeben sich, weil für die Winkel 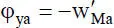 und
und 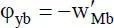 gilt.
gilt.
2.5.3 Trigonometrische und Hyperbelfunktionen für Stabelemente
Im Folgenden wird für drei Sonderfälle gezeigt, dass in den Funktionen für die Ver-formungen auch folgende Funktionen vorkommen können:
Trigonometrische Funktionen: sin x und cos x
Hyperbelfunktionen: sinh x und cosh x
Biegung mit Drucknormalkraft nach Theorie II. Ordnung und Stabilitätsfall Biegeknicken
Nach Abschnitt 2.4.4, Gl. (2.15), lautet die DGL für die Durchbiegungen in z-Richtung:
(2.32) 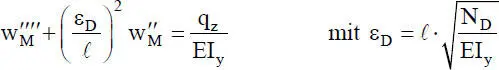
Bekanntlich setzt sich die Lösung dieser DGL aus zwei Anteilen zusammen:
Читать дальше



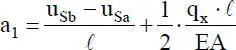
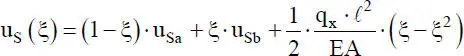
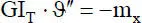
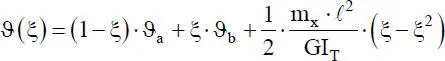
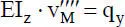
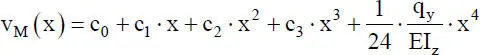
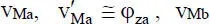 und
und 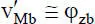 . Unter Verwendung der Randbedingungen
. Unter Verwendung der Randbedingungen 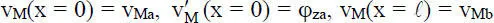 , und
, und 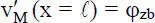 können die Integrationskonstanten in Gl. (2.29)ersetzt werden. Mit der dimensionslosen Koordinate ξ = x/ ℓ erhält man die folgende Funktion für die Durchbiegungdes Stabelementes in y-Richtung:
können die Integrationskonstanten in Gl. (2.29)ersetzt werden. Mit der dimensionslosen Koordinate ξ = x/ ℓ erhält man die folgende Funktion für die Durchbiegungdes Stabelementes in y-Richtung: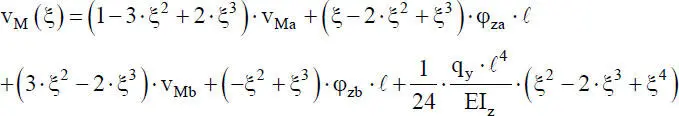

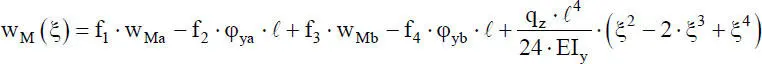
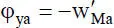 und
und 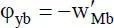 gilt.
gilt.